Массивы, числа и цвета

Созданный выше массив img можно отобразить как изображение в оттенках серого с помощью ImageView. Но если вы выполняете примеры в Juno или IJulia, то видите, что img выводится не как изображение, а как представленный выше массив чисел. Массивы «обычных чисел» не отображаются графически, так как могут представлять что-то числовое (например, матрицу в линейной алгебре), а не изображение. Чтобы указать, что объект должен быть представлен графически, преобразуйте тип элементов в цвета из пакета Colors:

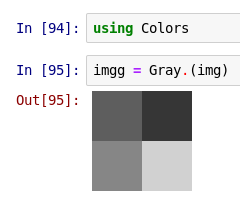
Здесь мы использовали цвет Gray, чтобы указать, что массив должен интерпретироваться как изображение в оттенках серого. (Имейте в виду, что пакет Colors экспортируется вместе с Images, поэтому можно просто использовать директиву using Images.)

Что делает Gray на внутреннем уровне? Для наглядности можно вывести «необработанный» объект в виде текста:

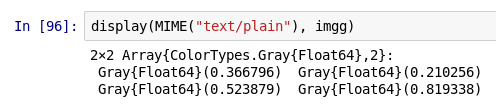
(Пользователи Juno или интерфейса командной строки Julia REPL увидят это представление сразу же.)

Как видите, это массив 2×2 объектов Gray{Float64}. Вам может быть любопытно, какое представление у этих объектов Gray. В командной строке REPL оно выглядит так (эта же самая команда работает в IJulia):

dump выводит «внутреннее» представление объекта. Как видите, Gray — это тип (строго говоря, неизменяемая структура struct) с единственным полем val; для Gray{Float64} val — 64-битное число с плавающей запятой. Использовать val напрямую не рекомендуется: извлечь значение Float64 можно с помощью функции доступа real или gray (почему вторая функция так называется, станет понятнее при обсуждении цветов RGB).

Какие издержки влекут эти объекты?

Ответ — никаких: сами по себе они не занимают памяти и обычно не требуют дополнительных вычислений. «Оболочка» Gray — это просто интерпретация значений, помогающая понять, что объект должен отображаться как изображение в оттенках серого. И действительно, img и imgg оказываются равными:

Этим данная тема не исчерпывается, но мы продолжим разговор о ней при обсуждении преобразований и представлений.

Gray — не единственный цвет во вселенной:

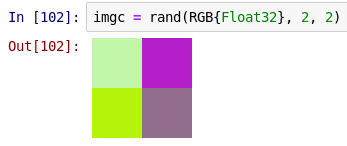
Давайте выведем imgc как текст (в данном случае в REPL):

Здесь можно увидеть одно из основных отличий подхода к изображениям в Julia от ряда других популярных фреймворков: в imgc нет измерения массива, выделенного для «цветового канала». Вместо этого каждый элемент массива представляет всю полноту информации о пикселе. Это позволяет упростить логику многих алгоритмов, а иногда одна реализация может работать как для цветных изображений, так и для изображений в оттенках серого.

Получить отдельные цветовые каналы можно по именам полей (r, g и b), но, как вы скоро увидите, более универсальным подходом является использование функций доступа:

Пакет Julia Colors позволяет представить один и тот же цвет по-разному, что может упростить взаимодействие с другими инструментами. Например, в некоторых библиотеках C допускается или общепринята другая очередность цветовых каналов:

Красный, зеленый и синий цвета могут также упаковываться вместе с пустым альфа-каналом (означающим прозрачность) в одно 32-разрядное целое число:

Здесь каналы следуют в следующем порядке от первого (первые две шестнадцатеричные цифры после 0x) до последнего (последние две шестнадцатеричные цифры): альфа, красный, зеленый, синий:

Эти значения близки к каналам в c, но округлены — каждый канал кодируется всего 8 битами, поэтому неизбежна некоторая аппроксимация точного значения с плавающей запятой.

У c24 нет поля r, но мы все же можем получить красный канал с помощью red:

Поначалу это может показаться несколько странным, поэтому давайте разберемся внимательно. Во-первых, обратите внимание, что часть этого значения в виде числа с плавающей запятой соответствует (с точностью до округления) значению red(c). Часть N0f8 означает следующее: «нормализованное (Normalized), с 8 битами дробной части (8 fractional bits) и 0 битами для представления значений более 1». Это число с фиксированной запятой — оно похоже на число с плавающей запятой, но запятая не «плавает». На внутреннем уровне такое число представлено как 8-разрядное целое число без знака UInt8:

(Обратите внимание, что N0f8 — это сокращение; полное имя типа — Normed{UInt8, 8}.) N0f8 означает, что это 8-разрядное целое число должно интерпретироваться как значение в диапазоне от 0 до 1, где 0 соответствует 0x00, а 1 — 0xff. Такая интерпретация влияет на то, как число используется в арифметических операциях и преобразуется в другие значения и обратно. Иначе говоря, для r верно следующее:

практически во всех случаях (однако см. A note on arithmetic overflow).

Это обстоятельство имеет одно очень важное последствие: во многих других фреймворках для работы с изображениями «смысл» изображения зависит от того, как оно хранится, однако в Julia он может быть независим от представления в памяти. Например, на другом языке или в другом фреймворке следующая последовательность:

может давать следующие изображения:

Изображение справа выглядит белым, потому что типы с плавающей запятой интерпретируются как лежащие на цветовой шкале 0—​1 (а все элементы в img имеют значение 1 или более), в то время как тип uint8 интерпретируется как лежащий на цветовой шкале 0—​255. К сожалению, два массива с идентичными числовыми значениями имеют совершенно разный смысл как изображения.

Многие фреймворки предлагают вспомогательные функции для преобразования изображений из одного представления в другое, но при сравнении изображений это может быть источником ошибок: в большинстве числовых систем само собой разумеется, что 255 != 1.0, и этот факт означает, что иногда нужно быть очень осторожным при преобразовании одного представления в другое. Напротив, при использовании данных пакетов Julia способ кодирования изображений с помощью чисел с плавающей запятой или 8-разрядных (либо 16-разрядных) чисел с фиксированной запятой не влияет на смысл: 0 всегда означает «черный», а 1 или большее значение всегда означает «белый» или «насыщенный».

Однако это не мешает вам создавать пиксели со значениями вне данного диапазона:

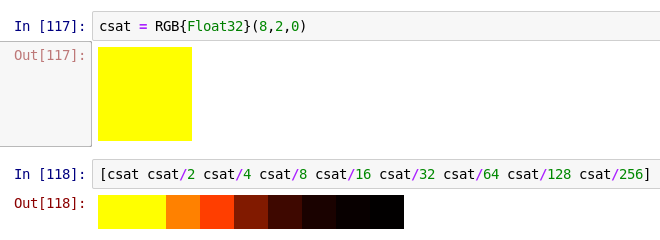
Обратите внимание, что первые два оттенка желтого выглядят одинаково, потому что и красный, и зеленый цветовые каналы имеют значение 1 или более и, следовательно, являются насыщенными.

Однако следует учитывать, что для целочисленных входных значений по умолчанию используется тип элементов N0f8, который не может представлять значения вне диапазона от 0 до 1:

В сообщении об ошибке поясняется, как устранить распространенную ошибку, возникающую при попытке построить красный цвет как RGB(255, 0, 0). В Julia для этого всегда следует использовать RGB(1, 0, 0).

16-разрядные изображения можно выразить через тип N0f16. Сравним максимальные значения (typemax) и наименьшую разницу (eps), которые можно представить с помощью типов N0f8 и N0f16:

Как видите, этот тип также имеет максимальное значение 1, но более высокую точность с гораздо меньшим интервалом между соседними числами.

Многие камеры (особенно научные) сейчас возвращают 16-разрядные значения. Однако некоторые камеры предоставляют информацию не на все 16 разрядов; например, камера может быть 12-разрядной и возвращать значения от 0x0000 до 0x0fff. При использовании типа N0f16 последнее значение будет отображаться как почти черное:

Так как камера является насыщенной, это может вносить путаницу, ведь такое значение вместо этого должно отображаться как белое.

Это служит еще одним свидетельством одной из основных проблем, которая возникает, когда предполагается, что представление (16-разрядное целое число) также описывает смысл числа. В Julia эта связь разрывается благодаря использованию различных числовых типов с фиксированной запятой. В данном случае такие значения естественным образом выражаются с помощью чисел с фиксированной запятой с 12 битами дробной части. В результате остается 4 бита для представления значений больше 1, поэтому такой числовой тип называется N4f12:

Как видите, максимальное значение, выражаемое через N4f12, составляет приблизительно 16 = 2^4.

При использовании интерпретации N4f12 для 16 бит цвет правильно отображается как белый:

а в арифметических операциях интерпретируется как 1. Хотя базовое представление будет тем же (0x0fff), мы можем наделить число определенным смыслом посредством его типа.

Иногда могут быть полезны цветовые значения вне диапазона от 0 до 1. Например, если нужно вычислить усредненный цвет изображения, естественным подходом будет сложить все пиксели, а затем разделить результат на их количество. На промежуточном этапе сумма, как правило, будет представлять цвет далеко за пределами насыщения.

Важно отметить, что при арифметических операциях с числами типа N0f8, так же как и с числами типа UInt8, происходит переполнение:

Поэтому значения рекомендуется накапливать в соответствующем типе с плавающей запятой, например Float32, Gray{Float64} или RGB{Float32}.