Nonlinear Reluctance
具有磁滞的非线性磁阻。
blockType: AcausalElectricPowerSystems.Passive.NonlinearReluctance
图书馆路径: |
磁阻线性参数化方程
磁阻线性参数化方程有以下形式:
,
,
,
哪里
-
-磁感应;
-
-磁常数;
-
-相对磁导率;
-
-场强;
-
-组件中的磁动势(MDS);
-
-模拟截面的有效长度;
-
-磁通量;
-
-模拟截面的有效截面积。
一个饱和点磁阻参数化方程
该参数化模拟具有两种状态的线性电阻。 在不饱和状态下,材料具有给定的相对磁导率。 在饱和状态下,相对渗透率为 .
具有单个饱和点的磁阻方程具有以下形式
,
,
.
如果
-
.
否则的话,
-
,
哪里
-
-饱和时的磁感应;
-
-饱和时的磁阻;
-
-相对磁导率没有饱和。
磁滞磁阻参数化方程
磁感应和磁电动势的方程有以下形式:
,
.
接下来,该块实现了之间的连接 和 根据Gills-Atterton方程。 连接的方程 和 随着铁心磁化,它具有的形式:
,
哪里 -磁芯磁化。
磁化导致感应的增加,其量值取决于电流值和场强的历史。 . 要定义 在任何给定时间,在块中使用Gills–Atterton方程。
下图显示了一个典型的关系图。 和 .
在这种情况下,在初始时刻,磁化强度为零,因此图形从 . 随着场强的增加,图形趋向于增加的滞后曲线,并且随着变化率的变化 -减少。 上升曲线和下降曲线之间的差异是由于依赖性 从轨迹历史。 在物理上,这种行为对应于这样一个事实,即磁芯中的磁偶极子与场强的增加对齐,但不会随着场强的降低而完全返回到它们的原始位置。
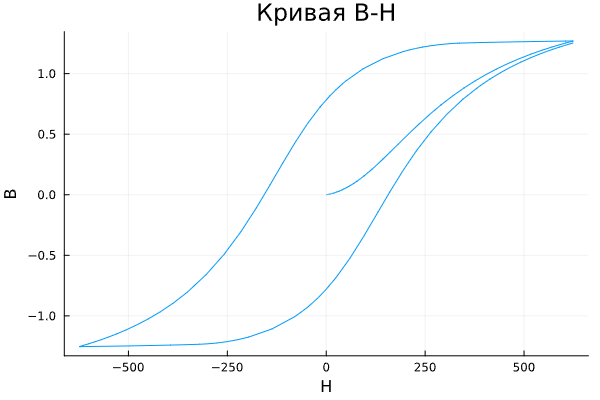
Gills-Atterton方程的起点是将磁化效应分成两部分,其中一部分是有效场强的函数( ),而另一个是不可逆转的部分,取决于历史:
.
变量 它被称为无磁滞磁化,因为它没有磁滞。 它由有效场强的电流值的以下函数描述 :
.
此函数使用极限值设置饱和曲线。 和饱和点,由值确定 -无滞后曲线的形状系数。 近似地,可以假设它描述了两个滞后曲线的平均值。 这些值在块的接口中设置 由 还有点 和 .
参数 它是磁化的可逆性系数,决定了行为的哪一部分决定了 哪一个是不可逆转的成员 . 在Gills-Atterton模型中,不可逆项由场强的偏导数确定:
.
为 , .
为 , .
该方程与标准一阶微分方程的比较表明,随着场强的增加 不可逆转的成员 尝试跟踪可逆成员 ,但具有可变增益 . 增益因子导致滞后点,其中 改变标志。 形成不可逆特性的主要参数是 ,其被称为体积耦合系数。 参数 它被称为域间耦合系数,也用于确定在构建无滞后曲线中使用的有效场强。:
.
意义 它影响磁滞回线的形状:随着值的增加,与B轴的交点向上移动。 但是,应该指出的是,为了稳定,有必要使用一个成员 这应该是积极的,当 和负时 . 因此,并非所有值都是 可接受,典型的最大值约为 1e-3.
求Gills-Atterton方程系数近似值的过程
方程系数的近似值可以使用以下过程确定:
-
指定参数的值 Anhysteretic b-h梯度当H为零( 由 )和一个时期 在无滞后的B-H曲线上。 这些值是在块初始化期间从这些值确定的 和 .
-
设置可逆磁化参数的*系数的值, ,从而在从一个点开始模拟时实现导数B-H的正确初始值 . 意义 近似等于当H为零 *时导数的这个初始值与 非系统性B-h梯度的比率。 意义 应该还有更多
0而且更少1. -
设置参数 体耦合系数K 的值,大约等于 何时 在一个增加的滞后曲线上。
-
从一个非常小的值开始 并逐渐增加以调整值。 越线时 . 典型值范围从
1e-4以前1e-3. 过大的值导致B-H曲线的导数趋于无穷大的事实,这与物理学相矛盾并导致程序执行中的错误。
为了获得与给定B-H曲线的良好匹配,您可能需要多次执行这些步骤。
参数
有效长度-模拟通行段的有效长度:q[<br>] 0.032m(默认)
磁芯的有效长度,即磁路的平均长度。
值必须是正的,而不是无限的。
有效截面积-通过的有效截面积:q[<br>] 1.6e+5m2(默认)
磁芯的有效截面积,即磁通路径的平均面积。
值必须是正的,而不是无限的。
功率记录的平均周期-用于平均通过的激励周期:q[<br>] 0s(默认)
计算滞后损耗的平均周期。 这些损失与封闭在B-H轨迹中的面积成比例。 如果单元以已知的固定频率激励,那么为了计算滞后损耗,该值可以设置为等于相应的激励周期。 在这种情况下,单位登记滞后损失每AC周期在变量 [医]能量消化. 如果使用固定步长求解器,则该值必须是仿真步长的整数倍。
如果设备未以已知的固定频率通电,请将此参数设置为0。 在这种情况下,单位将设置值 [医]能量消化 等于零,并且您将能够通过对注册变量进行后处理来计算实际的滞后损耗。 电源安装.
依赖关系
如果将 Parameterized by 参数设置为 具有滞后的非线性磁阻(JA模型).
通过—参数化B-H通过曲线的方法参数化:q[<br>] 磁阻(B-H曲线)(默认) | 线性磁阻 | 单饱和点的磁阻 | 具有滞后的非线性磁阻(JA模型)
的B-H曲线参数化方法。
相对磁导率—pass的相对磁导率:q[<br>] 5000(默认)
相对磁导率。
值必须是正的,而不是无限的。
依赖关系
如果将 Parameterized by 参数设置为 线性磁阻.
不饱和相对磁导率-pass的相对磁导率:q[<br>] 5000(默认)
不饱和电感器的相对磁导率.
依赖关系
如果将 Parameterized by 参数设置为 单饱和点的磁阻.
饱和时的磁通密度-磁感应强度:q[<br>] 1.5Tl(默认)
饱和电感器的磁感应.
值必须是正的,而不是无限的。
依赖关系
如果将 Parameterized by 参数设置为 单饱和点的磁阻.
磁场强度向量,H-磁场强度传递值的向量:q[<br>] [0, 200, 400, 600, 800, 1000] 车辆(默认)
磁场强度, ,被给定为具有与磁感应值的向量中相同的元素数的向量, . 矢量应该从零开始,单调增加。
依赖关系
如果将 Parameterized by 参数设置为 磁阻(B-H曲线).
磁通密度向量-磁感应强度值的向量通过:q[<br>] [0, 1.25, 1.35, 1.44, 1.48, 1.49] Tl(默认值)
磁感应, ,被定义为与磁场强度矢量具有相同元素数的矢量, . 矢量应该从零开始,单调增加。
依赖关系
如果将 Parameterized by 参数设置为 磁阻(B-H曲线).
H为零时的非线性B-H梯度 是无滞后B—h曲线接近零场强的导数通:q[<br>] 0.005m*Tl/A(默认)
无滞后B-H曲线的梯度约为零场强。 定为增加和减少滞后曲线的梯度的平均值。
依赖关系
如果将 Parameterized by 参数设置为 具有滞后的非线性磁阻(JA模型).
无磁滞B-h曲线上的磁通密度点 是无磁滞b-H通过曲线上某点的磁感应强度值:q[<br>] 1.49Tl(默认)
指定在无磁滞曲线上的点处的磁感应的值。 最准确的选择是选择高场强的点,当增加和减少滞后曲线重合时。
依赖关系
如果将 Parameterized by 参数设置为 具有滞后的非线性磁阻(JA模型).
对应场强-对应场强通过:q[<br>] 1000A/m(默认)
参数指定的点的对应场强 在非系统性B-H曲线上的通量密度点。
依赖关系
如果将 Parameterized by 参数设置为 具有滞后的非线性磁阻(JA模型).
*可逆磁化系数,c*为磁化通过的可逆性系数:q[<br>] 0.1(默认)
可逆的磁化比例。 值必须大于零且小于一。
依赖关系
如果将 Parameterized by 参数设置为 带滞后的非线性磁阻(JA模型).
*体耦合系数,K*为通的体耦合系数:q[<br>] 200A/m(默认)
Gills-Atterton模型的一个参数,用于确定b-h曲线与零磁感应线相交的场强的大小。
依赖关系
如果将 Parameterized by 参数设置为 带滞后的非线性磁阻(JA模型).
*域间耦合因子,α*为域间耦合通系数:q[<br>] 0.0001(默认)
Gills-Atterton参数,它影响曲线B-H与零场强线的交点。 典型值范围从 1e-4 以前 1e-3.
依赖关系
如果将 Parameterized by 参数设置为 具有滞后的非线性磁阻(JA模型).
插值选项-通过插值方法:q[<br>] 线性(默认情况下) | 光滑
块用于确定在前述向量中未指定的中间时间点的值的插值方法。:
-
线性的-通过使用线性函数优先计算性能。 -
光滑-由于获得具有连续一阶导数的连续曲线而导致精度的优先级。
