放大器参数评估
放大器参数估计 
—这是一个*Engee*应用程序，旨在根据测量数据分析功率放大器（UM）的特性，以及构建放大器模型，并有可能在*Engee*仿真环境中使用它们。 支持信号分析、模型参数设置、结果可视化和系数导出供以后使用。
要打开应用程序，请转到*Engee*工作区，并在该部分的左上角 Engee 应用 
选择 放大器参数估计 :
用途及使用范围
当通过功率放大器（UM）传输信号时，特别是在接近饱和的模式下，会发生非线性失真。 这导致两个关键效果:
-
将信号频谱扩展到带宽限制之外违反了频谱掩码(ACLR)要求;
-
带内失真和传输质量恶化-相邻信道（ACPR）功率增加。
为了提高发射机的能效，放大器通常工作在接近饱和的地方，出现非线性效应。 利用数字信号预失真(DPD)方法解决了该问题。 该方法的目的是预先改变（扭曲）输入信号，以便在通过真实的非线性信号后，输出信号尽可能接近理想的线性响应。 这使您可以:
-
提高放大器的效率;
-
减少非线性失真;
-
降低信道间干扰的水平;
-
确保符合传输标准。
该应用程序支持多种放大器模型自适应调谐算法:
-
RLS—递归最小二乘法;
-
LMS—经典最小二乘法;
-
NLMS-归一化LMS;
-
RPEM—递归误差预测方法;
-
*正则化RLS*是对具有噪声容限的RLS的修改。
这些方法允许您根据输入和输出信号动态调整模型参数。
还支持三种模型架构:
| 建筑设计 | 资料描述 |
|---|---|
P（多项式） |
无记忆多项式模型适用于没有明显滞后的简单情况。 |
MP(记忆多项式) |
增加了放大器"记忆"的效果，提高了建模时间依赖性的准确性。 |
GMP（广义记忆多项式） |
具有额外交叉构件的扩展架构-用于复杂的扭曲。 |
算法和体系结构组合的选择会影响模型的准确性。 评估标准通常是*NMSE*度量（归一化均方根误差）。
因此，应用程序 放大器参数估计 它允许您使用真实和合成数据对数字前图像系统进行建模和调整。
术语和缩写
-
DPD（数字预失真）-数字信号预失真，一种补偿放大器非线性失真的方法。
-
NMSE（归一化均方误差）是模型精度的指标，以分贝为单位。
-
PAPR(峰均功率比)-信号功率的峰值与其平均值的比率。
-
ACLR(相邻信道泄漏比)-相邻频率信道中的辐射水平。
-
Acpr(相邻信道功率比)-在相邻信道的功率的比率对主要一个。
-
*AM-AM*是输出振幅对输入的依赖性（振幅-振幅特性）。
-
*AM-PM*是输出相位对输入振幅（振幅-相位特性）的依赖性。
应用程序界面
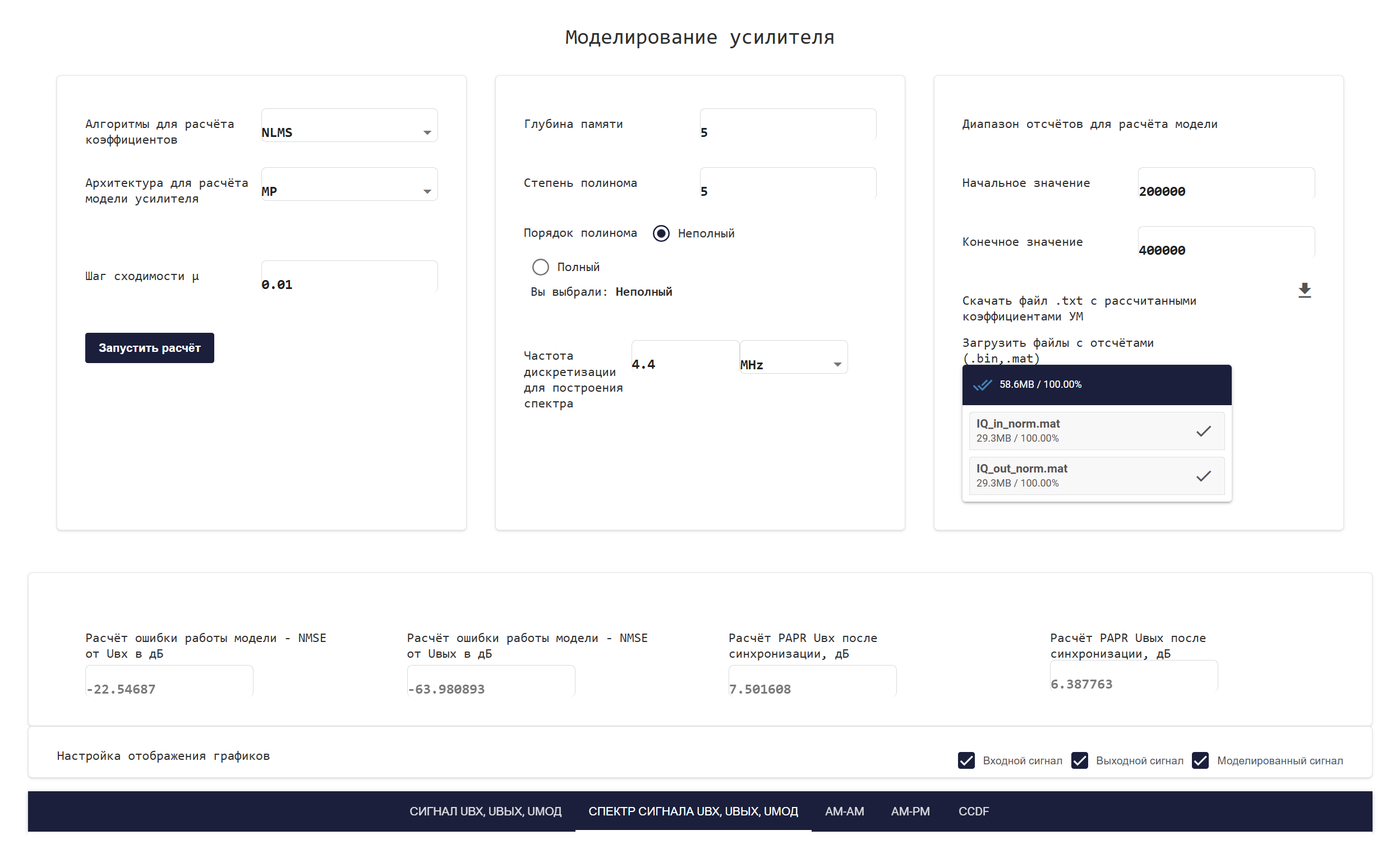
应用程序界面大致可以分为五个部分:
-
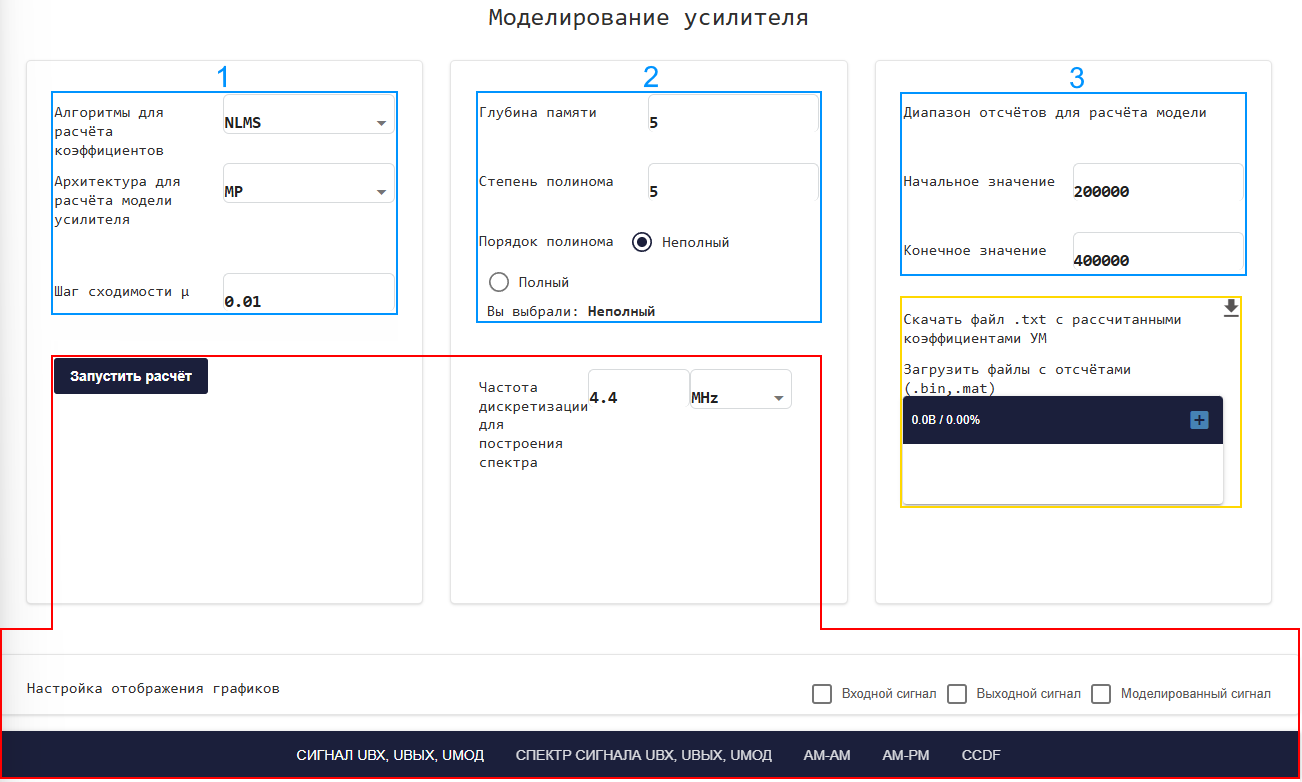
黄色部分用于下载带有amp计数和下载的文件。带有UM系数的txt文件;
-
三个蓝色部分用于调整放大器模型。;
-
红色部分是模型计算的开始，用于绘图的频谱信号的采样频率的控制，以及图形菜单本身。
接下来，让我们来看看如何使用界面与应用程序一致地工作。
使用应用程序
加载输入数据
要开始使用，请单击按钮下载两个包含放大器信号样本的文件 
在黄色部分:
-
IQ_in_norm-放大器输入端的信号样本; -
IQ_out_norm-放大器输出端的信号样本。
|
具有计数的文件必须命名 |
文件应同时上传。 为此，请通过以下方式选择它们 Ctrl+LKM 在打开的窗口中:
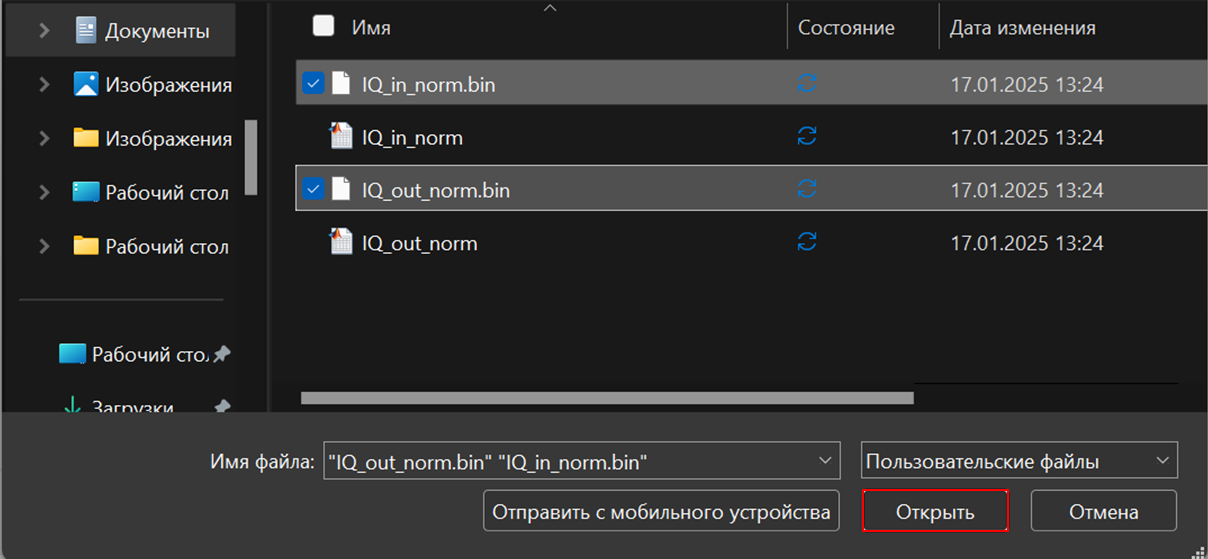
等待文件完全下载，下载指标应更改为✓:
在下载过程中 |
完成(✓) |
|---|---|
|
|
设置放大器模型
接下来，在蓝色部分逐步设置模型:
-
算法和体系结构的选择（第1节）-模型的类型和DPD方法（例如，NLMS）设置。 根据所选择的算法，您将需要指定收敛步骤或信任度和遗忘因子。 没有为Moore-Penrose算法指定其他参数。
-
模型参数（第2节）-为模型设置以下参数:
-
内存深度;
-
多项式的度;
-
多项式的阶数。
-
-
采样范围（第3节）-表示用于计算模型的采样范围（默认情况下：从
200000以前400000).
绘制图表
以下是可用的图形类型:
-
信号：输入，输出，模拟;
-
信号光谱;
-
AM-AM和AM-PM的特征;
-
累积分布函数(CCDF)。
采样率可以手动设置。:
Plotly库的经典功能将帮助您更方便地使用图形。:
-
-下载图形为PNG。 -
-选择一个区域并放大其内容的能力。 -
-用于在坐标平面上移动图形的工具。 -
-在坐标平面上放大。 -
-减小坐标平面的尺度。 -
-返回坐标平面的默认比例。 -
-重置坐标轴。
图表示例
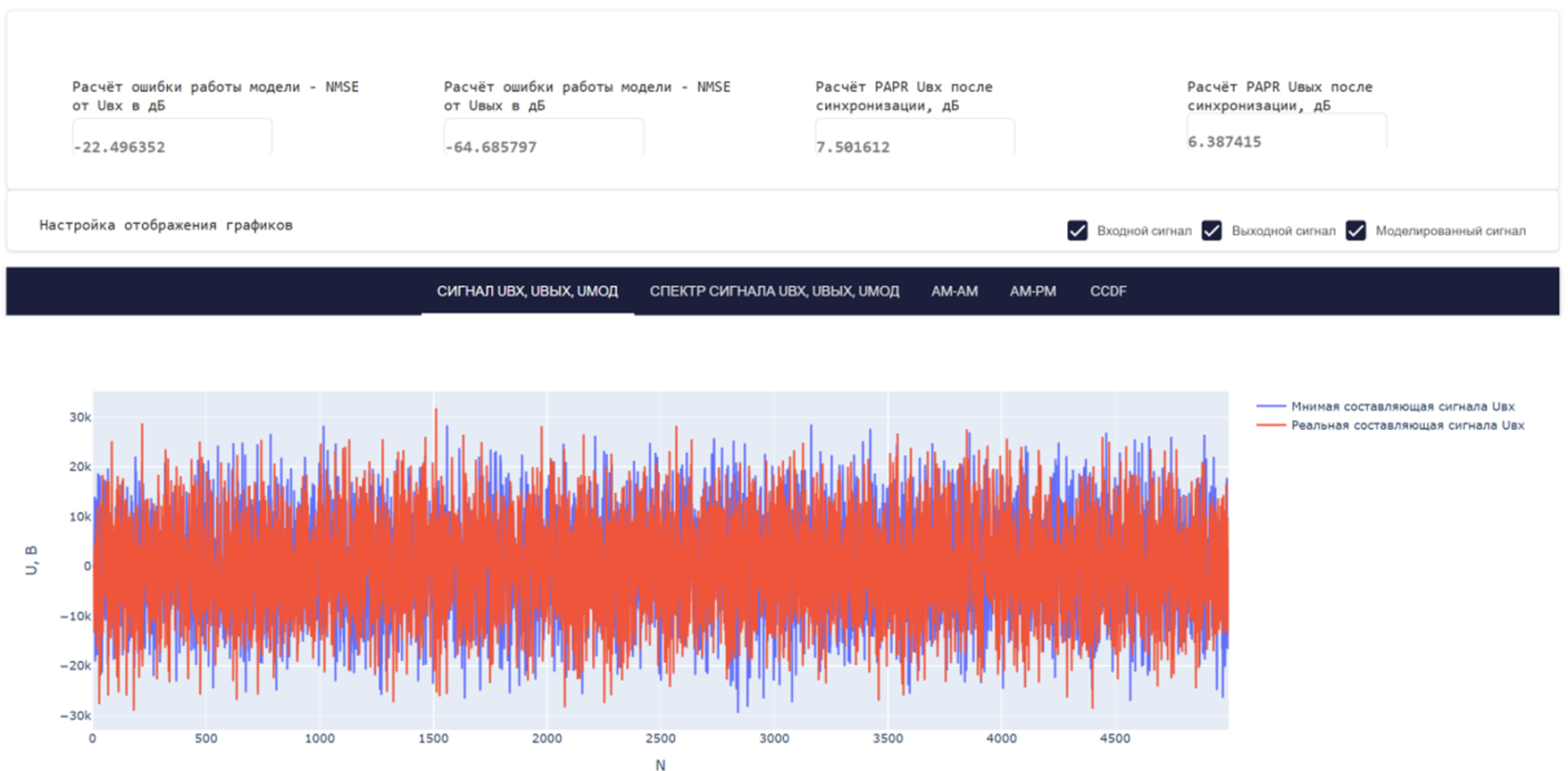
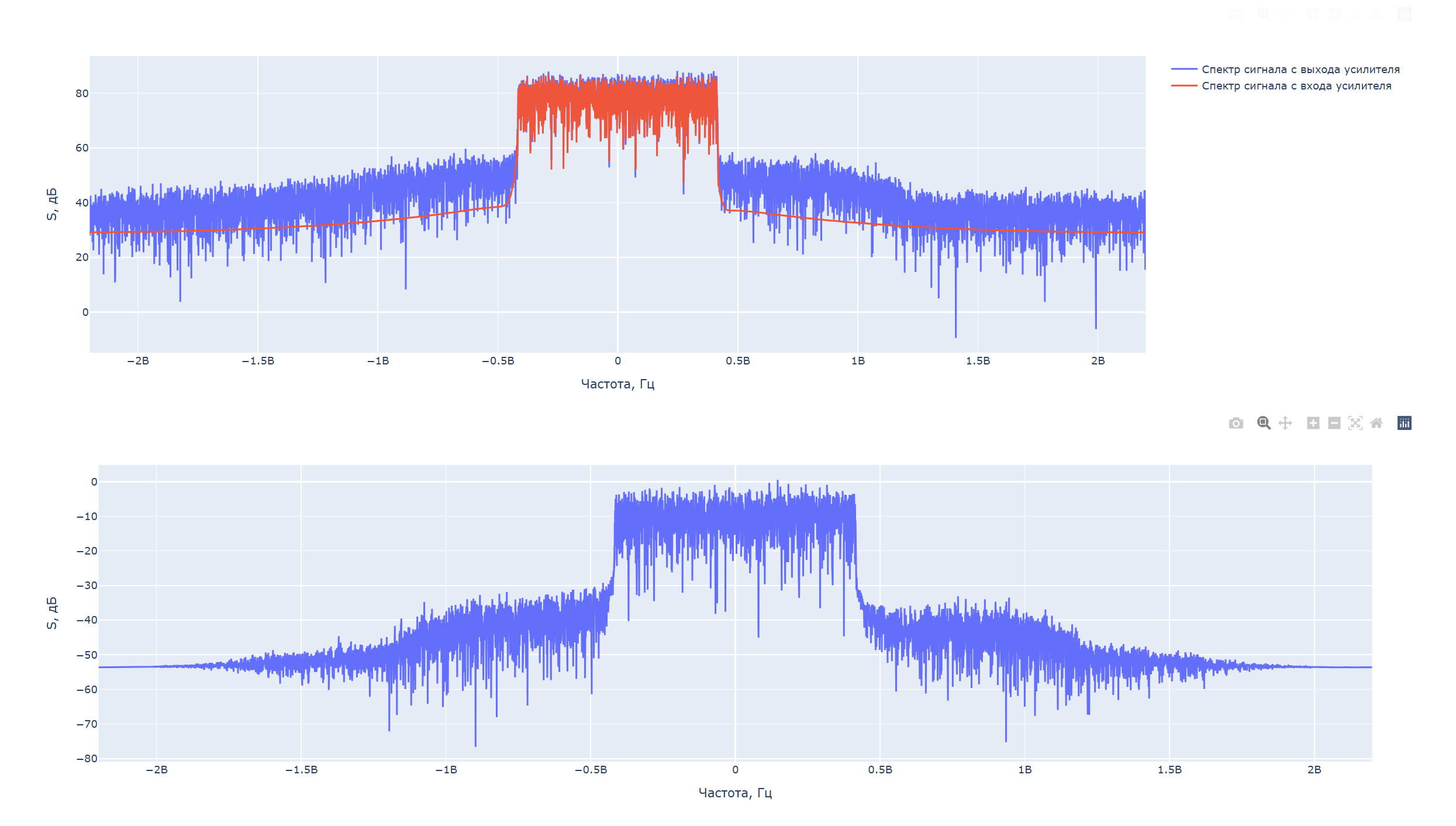
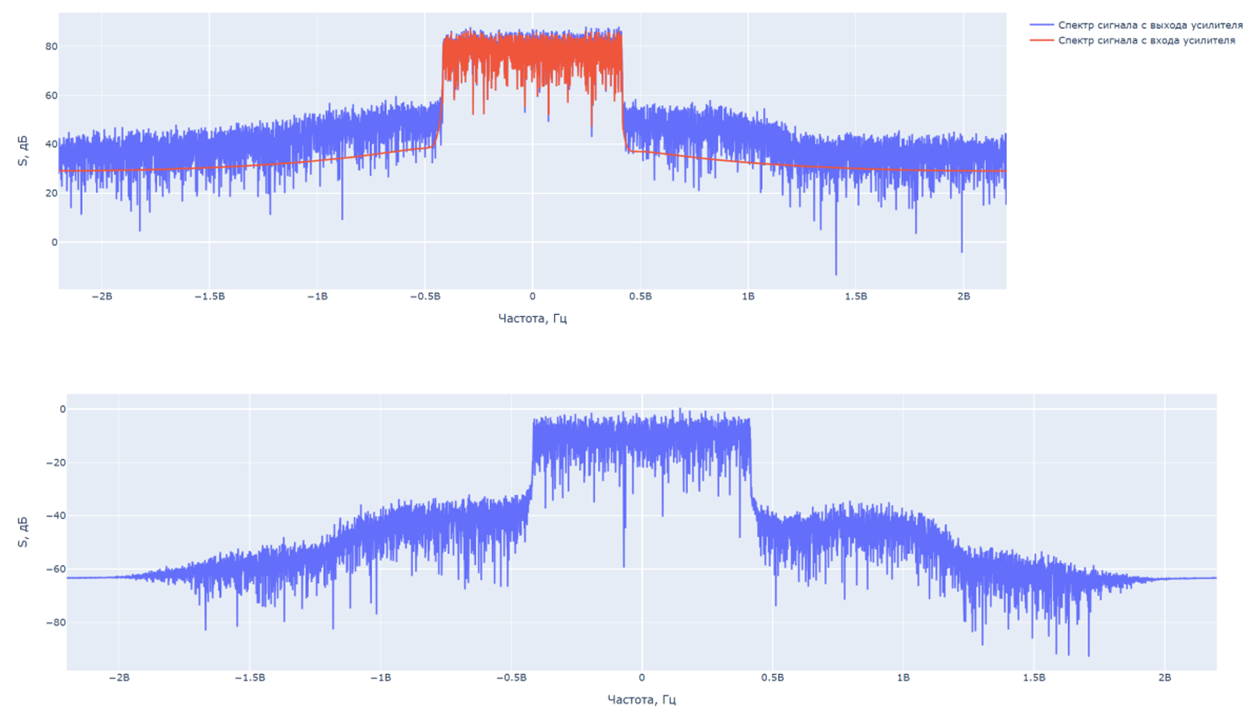
信号频谱Uinput,Uoutput,Umod:
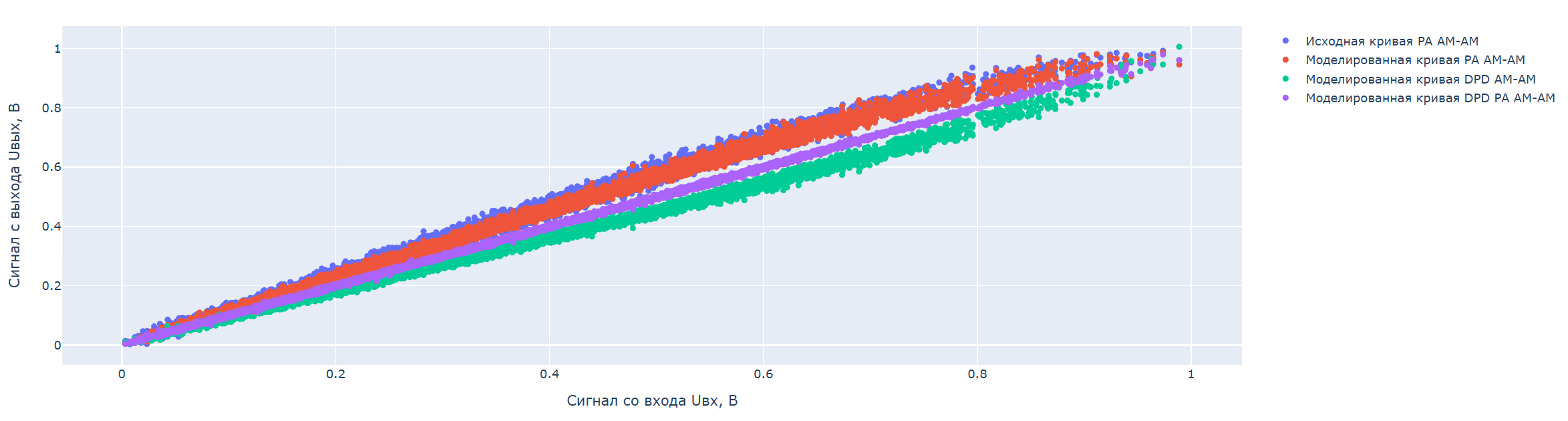
AM-AM的振幅-振幅特性:
AM-PM的幅相特性:
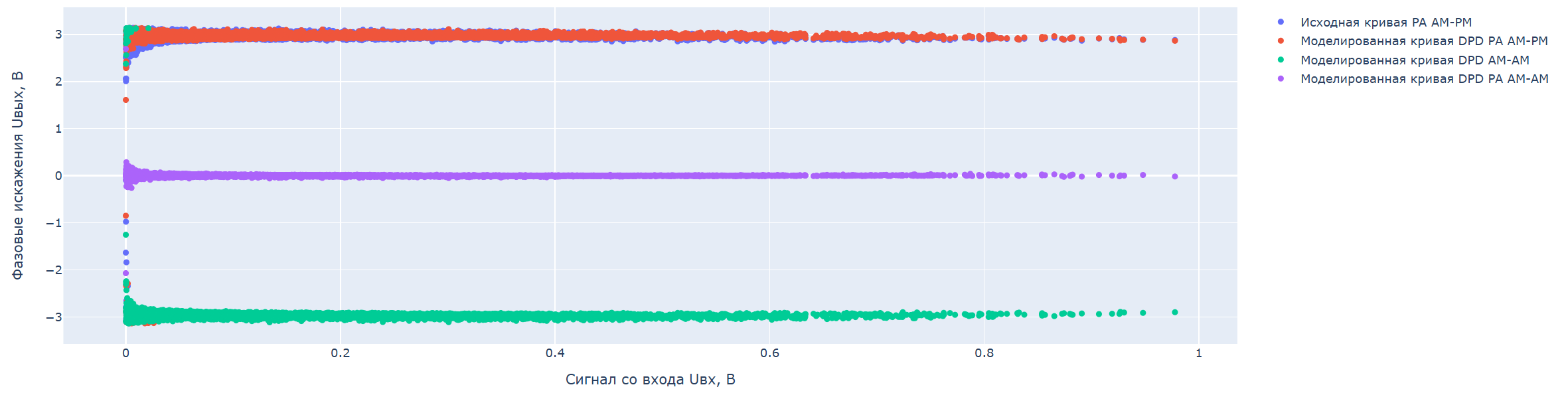
累积概率分布函数CCDF:
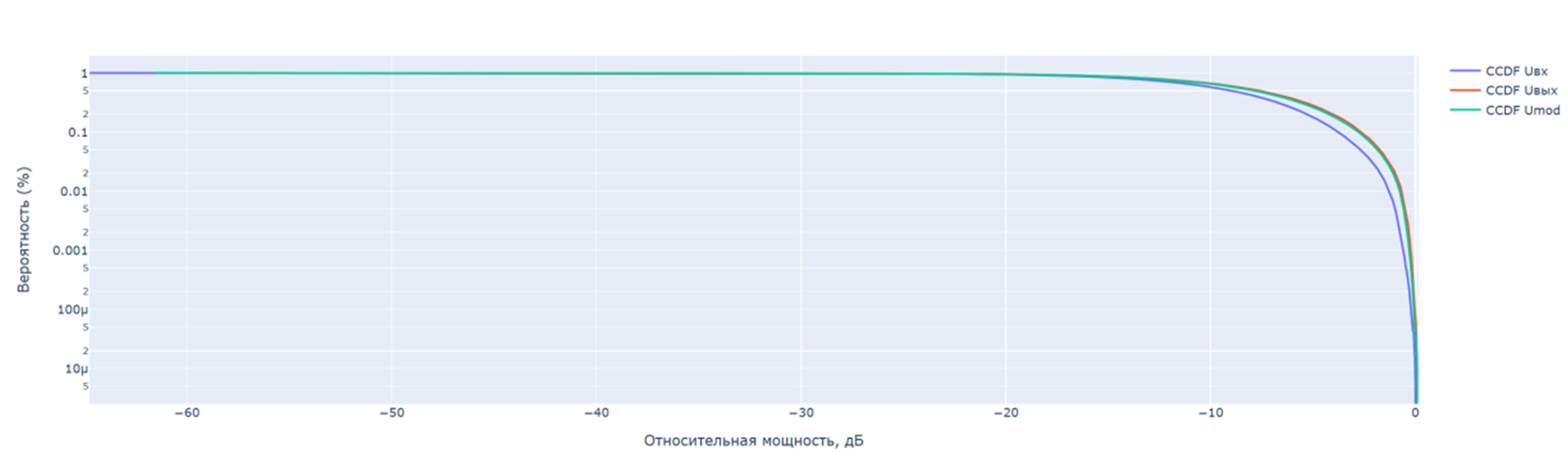
为了评估放大器模型的效率，自动计算以下值：以dB为单位的归一化均方根误差NMSE，输入、输出和模拟信号的峰值因子PAPR，例如:
