从AnyMath中的求解器开始
什么是求解器,它的用途是什么?
求解器 是计算 AnyMath 模型动态行为的工具。 求解器的选择及其设置会显着影响最终解的准确性和获取速度。 一个不成功的选项甚至可能导致一个错误的决定。 没有适用于所有任务的通用求解器,因此考虑到建模的目标和模型的功能,选择它非常重要。
|
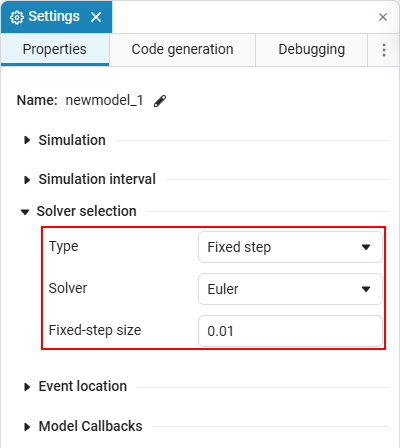
要查看当前求解器或选择另一个求解器,请打开窗口 设置
|
首先,您需要选择求解器的类型:
-
固定台阶 -步骤在整个计算实验中保持不变。 它们通常用于实时计算或检查数值解的正确性。 一般来说,它们是无效的,因为在整个建模间隔上的步骤受到个别更动态部分的要求的限制。 将步长减小到一定限度会增加解的精度,但自然会对计算速度产生负面影响。;
-
可变步长 —在计算实验期间自动调整步长,同时考虑到解的变化和局部积分误差的估计。 这种求解器减少了复杂区域的步进以保持精度,并增加了简单区域的步进以加快计算速度。
求解器也分为离散求解器和连续求解器。 对于没有连续状态的模型(没有连续积分器,传递函数等。),使用离散求解器,在其他情况下使用连续求解器。 如果您为没有连续状态的模型选择其中一个连续求解器,那么为了提高效率,它将根据初始选择自动替换为离散常数或可变步长。 尝试使用离散求解器计算连续状态模型将在开始计算时导致错误。
连续求解器可以基于各种类型的数值方法,其中值得单独强调:
-
* 隐式方法*-要求在每一步求解非线性代数方程组。 它们适用于刚性系统(有关详细信息,请参阅选择求解器),因为它们允许您使用大的步骤而不会损失稳定性,但每个步骤都需要大量的计算资源。 AnyMath*中的示例:ImplicitEuler,Trapezoid,TRBDF2,RadauIIA5,KenCarp,Kvaerno*,QNDF*,QBDF*,FBDF;
-
* 半隐式方法*-与隐式方法不同,它们需要在每个步骤求解线性代数方程组。 与隐式方程一样,它们也非常适用于刚性方程组。 一般来说,它们强烈依赖于雅可比矩阵计算的准确性。 例子在*AnyMath*:Rosenbrock*,Rodas*;
-
* 多步骤方法—-使用前几个步骤的数据来计算下一个步骤。 它们对于大型任务特别有效,但在存在多个事件的情况下,由于不断重新初始化,它们的速度会降低,因此不建议将它们用于具有不连续组件的模型。 AnyMath 中的示例:VCABM*,AB*,ABM*,QNDF*,QBDF*,FBDF。
*-一系列方法,例如,Kvaerno*表示Kvaerno3,Kvaerno4,Kvaerno5等。
选择求解器
在计算模型时,不可能在同一时间实现高精度和速度。 有必要通过选择合适的求解器在这些指标之间找到平衡点。 要做到这一点,您需要对它将解决的系统特性有一个很好的理解,即:
-
* 系统刚性*-刚性模型称为快速和慢速过程同时发生的模型,例如在化学反应或机电系统中。 对于这样的模型,显式方法由于稳定性范围小,需要非常小的步骤,因此最好使用隐式或半隐式方法,其步骤将仅受精度要求的限制。 如果系统的时间常数不同于
6和更多的数量级; -
* 模型大小*是唯一标识模型特定状态的连续变量的数量。 如果一个模型有超过
1000态变量。 它们越多,计算就越慢,特别是在使用隐式和半隐式方法时。 对于大型模型,最好在每个步骤中使用右侧(系统的导数)计算较少的方法。; -
* 对解决方案精度的要求*-确定数值和精确解决方案的接近度。 对绝对精度和相对精度的要求分别区分开来。:
-
绝对公差 (atol)-如果变量小于此设定值,则变量的局部误差估计值被视为零。 例如,对于具有一阶解分量的模型,通常使用该值 但一般来说,此设置对于每个特定模型都是单独的。;
-
相对宽容度 (rtol)-定义相对于变量值本身的可接受的局部误差。 近似设定值:
-
-精度低;
-
-高精度;
-
-非常高的精度。
更高的精度需要使用先进的求解器,这可以显着增加总计算时间。
-
-
-
* 解决方案中存在间隙*-一些库组件,例如 绝对 或 饱和度,其特征在于行为的突然突然变化,这导致解决方案中的间隙。 多步骤方法通常对此类任务不太有效。
选择可变步长求解器时,可以使用下表作为起点:
| 精度/刚性 | 非刚性 | 中等硬度 | 强硬 |
|---|---|---|---|
低 |
BS3 |
摇滚2 |
Luler,梯形,Rodas3,Rosenbrock23,TRBDF2 大尺寸:TRBDF2 |
平均 |
Tsit5,BS5,DP5 大尺寸:VCABM |
摇滚4 |
Rodas4,Rodas4p,KenCapr4 大尺寸:QNDF,QBDF |
高 |
DP8,Vern6,Vern7,Vern8,Vern9 大尺寸:VCABM |
Rodas5,Rodas5p,RadauIIA5,Kvaerno5 |
Rodas5,Rodas5p,RadauIIA5,Kvaerno5 大尺寸:QNDF,QBDF |
由于没有所有模型的通用求解器,您需要自己选择求解器,重点关注问题的细节,所需的精度和允许的计算时间。 在这种情况下,您不仅可以尝试来自一个单元格(在上表中)的求解器,还可以尝试来自相邻单元格的求解器以找到最优选项。 一个合理的解决方案是在性能和质量之间找到一个平衡点,这将允许正确和有效的建模。