Cholesky Factorization
Decomposition of a square Hermite positively definite matrix into triangular components.
Description
Block Cholesky Factorization uniquely decomposes the square Hermite positively defined input matrix S as
,
where:
-
- is a lower triangular matrix with positive diagonal elements.
-
- Hermite (complex-conjugate) transposed matrix L.
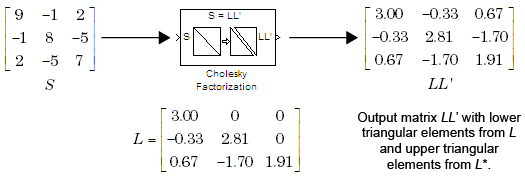
The block outputs a composite matrix with elements below the main diagonal of and elements above and on the main diagonal of .
The figure below shows the result of the block Cholesky Factorization (matrix LL').
Input signal requirements
The output of a block is considered valid (i.e. mathematically correct) only when its input has the following characteristics:
-
Hermite - the block does not check whether the input is Hermite; it uses only the diagonal and upper triangle of the input matrix to compute the output.
-
Diagonal elements are real - the block ignores any imaginary component of the diagonal elements.
-
Positive definite - the Non-positive definite input parameters sets the response to a non-positive definite input.
Response to non-positive definite input
To compute a valid output, the block algorithm requires a positively definite input. The Non-positive definite input parameter specifies the block’s response to a non-positive definite input:
-
Ignore- the simulation continues and no warning is issued. The result is not a valid decomposition. Partial decomposition will be present in the upper left corner of the output matrix.
-
Error- the error dialogue box is displayed and the simulation stops.
Ports
Input
S - initial matrix S
`matrix M by M
The input signal is in the form of a square matrix.
The algorithm requires the input matrix to be square and Hermite positively definite. The block uses only the diagonal and upper triangle of the matrix and ignores any imaginary component in the diagonal elements.
Data types: Float64
Parameters
Non-positive definite input - response to non-positive definite input matrix
Ignore (by default) | Warning | Error
The input matrix S must be Hermite positively definite.
When the input is not positively definite, the block reacts as follows:
-
Ignore- the simulation continues and no warning is issued. The result is not a valid decomposition. A partial decomposition will be present in the upper left corner of the output matrix.
-
Error- the error dialogue box is displayed and the simulation stops.
| The Non-positive definite input parameter is a diagnostic parameter. Like all diagnostic parameters, it is set to `Ignore'. |