LDL Factorization
Decomposition of a square Hermitian positive definite matrix into lower, upper and diagonal components.
blockType: LDLFactorization
|
Path in the library: |
Description
Block LDL Factorization uniquely decomposes the Hermitian positive definite input matrix How
Where:
-
— lower triangular matrix with single diagonal elements (unit triangular matrix);
-
— diagonal matrix;
-
— Hermitian (complex conjugate) transposed matrix .
Only the diagonal and bottom triangle of the input matrix are used. Any imaginary component of the diagonal elements is ignored.
The LDL decomposition requires half the calculations of the LU decomposition and is always stable. It is more efficient than the Cholesky decomposition, since it avoids calculating the square roots of diagonal elements.
Ports
Input
Port_1 is the original matrix S
matrix M by M
The input signal is in the form of a square matrix.
The algorithm requires the input matrix to be square and Hermitian positive definite. When the Input is not positively defined, the block reacts as specified by the input parameter Non-positive Definity.
Data types: Float64
Support for complex numbers: Yes
Output
Port_1 — output matrix
matrix M by M
The output is a composite matrix with elements below the main diagonal from , diagonal elements from and elements above the main diagonal from ,
Where:
-
— lower triangular matrix with single diagonal elements (unit triangular matrix).
-
— diagonal matrix.
-
— Hermitian (complex conjugate) transposed matrix L.
The output format is shown below for a 5 by 5 matrix.
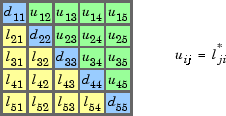
Data types: Float64
Parameters
Main
Non-positive definite input — reaction to a non-positively defined input matrix
Ignore (by default) | Warning | Error
Specifies the action when non-positively defined input parameters of the matrix occur:
-
Ignore— the simulation continues and no warning is issued. The result is not a valid decomposition. A partial decomposition will be present in the upper left corner of the output matrix. -
Warning— The simulation continues, but a warning message is displayed in the Engee command window. The result is not a valid decomposition. A partial decomposition will be present in the upper left corner of the output matrix. -
Error— the error dialog box is displayed and the simulation stops.
