Animation of fireworks using Makie

Makie is a popular visualization library in the julia ecosystem.
This example will cover topics such as:

Using color palettes (colormaps/colorschemes)
Create mp4 animations (as an alternative @gif in Plots.jl)
features of building point-by-point graphs (scatter):
size
- marker
- color
- alpha channel

The salute model as a system of differential equations

The salyut model in this example is described by a system of ordinary differential equations (ODES), which simulates the movement of particles under the influence of gravity, air resistance and horizontal wind. The system includes four variables: coordinates and , as well as their derivatives with respect to time (velocity and ). The equations have the form:

Here — acceleration of free fall, — air resistance coefficient, — the mass of the particle, — wind speed, — wind resistance coefficient. This system is solved numerically using the package DifferentialEquations.jl, which makes it possible to simulate the realistic behavior of fireworks particles after an explosion.

Installing dependencies and importing libraries

To work with animation and solving differential equations, we will need packages DifferentialEquations, CairoMakie and Random. We will install them, if they are not already installed, and import them.

import Pkg; Pkg.add(["DifferentialEquations","CairoMakie","Random"])
using DifferentialEquations
using CairoMakie
using Random

# Installing seed for reproducibility
Random.seed!(1945_2025)

Program structure

Our program consists of several key components: a set of fireworks, each of which contains particles, a trajectory is calculated for each particle, and the trajectory is a set of points. .

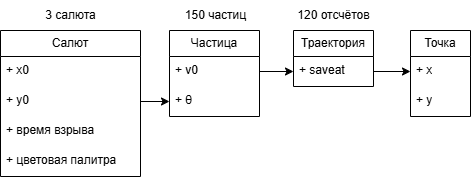
Defining the model and parameters

Defining the function particle_motion!, which describes the motion of particles according to the above system of ODES. We also set simulation parameters: acceleration of gravity, air resistance, particle mass, wind speed, and others.

# The function of particle motion taking into account the wind
function particle_motion!(du, u, p, t)
    g, k, m, v_w, k_w = p
    du[1] = u[3]  # dx/dt = v_x
    du[2] = u[4]  # dy/dt = v_y
    du[3] = -(k + k_w) / m * u[3] + k_w * v_w / m  # dv_x/dt = -(k + k_w)/m * v_x + k_w * v_w/m
    du[4] = -g - k / m * u[4]  # dv_y/dt = -g - k/m * v_y
end

# Parameters
g = 9.81      # acceleration of free fall
k = 0.1       # air resistance coefficient
m = 0.1       # particle mass
v_w = 0.1     # horizontal wind speed (m/s, positive — to the right)
k_w = 0.1     # wind resistance coefficient
n_fireworks = 3  # number of fireworks
n_particles_per_firework = 150  # particles for fireworks
v0_values = [1:2.5:25;]  # different initial speeds
tspan = (0.0, 1.5)  # total time interval
saveat = 0.0125  # fixed time step

Fireworks generation and color palette selection

Each salute is characterized by a random starting position ((x_0, y_0)), the time of the explosion, and a set of three color palettes. We use Makie.ColorSchemes to create a visually appealing effect, where the particles of each fireworks are painted in three different color schemes.

# List of palettes
available_palettes = [
    Makie.ColorSchemes.Reds,
    Makie.ColorSchemes.pink,
    Makie.ColorSchemes.solar,
    Makie.ColorSchemes.Blues
]

# Definition of fireworks
fireworks = []
for i in 1:n_fireworks
    # Random starting position
    x0 = rand(-12:12)
    y0 = rand(5:3:15)
    # Random burst time (between 0.0 and 75% tspan)
    explosion_time = rand(tspan[1]:0.1:0.75*tspan[2])
    # Choosing three random palettes for fireworks
    selected_palettes = shuffle(available_palettes)[1:3]  # choose 3 different palettes
    push!(fireworks, (x0=x0, y0=y0, explosion_time=explosion_time, palettes=selected_palettes))
end

Modeling of particle trajectories

For each salute, we simulate the trajectories of its particles by solving a system of ODES. Each particle is assigned one of three selected palettes to create a multicolored fireworks effect.

# Modeling the trajectories for each salute
all_trajectories = []
all_particle_palettes = []
for (idx, fw) in enumerate(fireworks)
    trajectories = []
    particle_palettes = []
    # We divide the particles into three groups for three palettes
    particles_per_palette = div(n_particles_per_firework, 3)
    for i in 1:n_particles_per_firework
        # Selecting the initial velocity from v0_values
        n_v = length(v0_values)
        v0 = v0_values[ceil(Int, (i - 1) / (n_particles_per_firework / n_v))%n_v+1] + rand(-2:0.25:2)
        θ = 2π * (i - 1) / (n_particles_per_firework / n_v) + rand(-0.1:0.001:0.1)  # random angle deviation
        u0 = [fw.x0, fw.y0, v0 * cos(θ), v0 * sin(θ)]  # starting position and speed
        prob = ODEProblem(particle_motion!, u0, tspan, (g, k, m, v_w, k_w))
        sol = solve(prob, Tsit5(), saveat=saveat)
        push!(trajectories, [(u[1], u[2]) for u in sol.u])
        # We assign a palette depending on the particle group
        palette_idx = (i - 1) ÷ particles_per_palette + 1
        if palette_idx > 3  # for the last set of particles
            palette_idx = 3
        end
        push!(particle_palettes, fw.palettes[palette_idx])
    end
    push!(all_trajectories, trajectories)
    push!(all_particle_palettes, particle_palettes)
end

Creating a scene and adding a starry background

Before creating the animation, we set a scene with a black background and add stars that will be displayed throughout the animation. This creates a night sky effect.

# Visualization
fig = Figure(backgroundcolor=:black)
ax = Axis(fig[1, 1], aspect=1, limits=(-20, 20, -20, 20),
    backgroundcolor=:black, xgridvisible=false, ygridvisible=false,
    xticksvisible=false, yticksvisible=false,
    xticklabelsvisible=false, yticklabelsvisible=false)

# Adding stars to the background
n_stars = 50  # Number of stars
x_stars = rand(-20:0.1:20, n_stars)  # Random x-coordinates
y_stars = rand(-20:0.1:20, n_stars)  # Random y-coordinates

Creating animations

Using the function record from CairoMakie to create MP4 animations. In each animation frame, we redraw the stars and fireworks particles that have already exploded, taking into account the tail effect and individual fading.

# Animation
total_frames = ceil((tspan[2] - tspan[1]) / saveat) + 1  # total number of frames
record(fig, "firework_with_wind.mp4", 1:total_frames-1) do frame_idx
    empty!(ax)
    # Redrawing the stars
    CairoMakie.scatter!(ax, x_stars, y_stars, marker=:star5, color=:yellow, markersize=5, alpha=0.5)
    # Current time in animation
    current_time = (frame_idx - 1) * saveat

    # We go through each salute
    for firework_idx in 1:n_fireworks
        fw = fireworks[firework_idx]
        trajectories = all_trajectories[firework_idx]
        particle_palettes = all_particle_palettes[firework_idx]
        # Checking to see if the fireworks have exploded
        time_since_explosion = current_time - fw.explosion_time
        if time_since_explosion >= 0
            # We calculate the time index relative to the time of the explosion
            i = Int(round(time_since_explosion / saveat)) + 1
            # We limit i to the length of the trajectory
            i = min(i, length(trajectories[1]))
            # Individual fading for each fireworks display
            if time_since_explosion >= 0
                fading_start = 0.6  # 60% of the visibility time
                fading_duration = 0.4  # the remaining 40% for fading
                k_fading = time_since_explosion < fading_start ? 1.0 : max(0.0, 1.0 - (time_since_explosion - fading_start) / fading_duration)
                # We limit the length of the tail: we display the last 24 positions
                for (traj, palette) in zip(trajectories, particle_palettes)
                    for j in max(1, i - 24):i
                        alpha = k_fading * (0.1 + 0.9 * exp(-0.4 * (i - j)))
                        markersize = 2 + 3 * exp(-0.5 * (i - j))
                        t = i > 1 ? (j - max(1, i - 14)) / (i - max(1, i - 14)) : 1.0
                        color = palette[t]
                        CairoMakie.scatter!(ax, [traj[j]], markersize=markersize, color=color, alpha=alpha)
                    end
                end
            end
        end
    end
end

The animation may take a certain amount of time, after which the file will be created. "firework_with_wind.mp4"

Conclusion

In this example, we created a fireworks animation using the ecosystem Makie with a backend CairoMakie. We've learned how to simulate particle motion using differential equations, apply color palettes for visual effect, and create MP4 animations. This approach can be adapted for other visualization tasks, such as modeling planetary motion, simulating explosions, or creating artistic animations.