Построение векторной диаграммы асинхронного двигателя
В этом примере представлено построение вращающейся векторной диаграммы асинхронного двигателя с короткозамкнутным ротором (АДКЗ) для одной фазы в статическом режиме.
Введение
Векторная диаграмма АДКЗ иллюстрирует взаимосвязь векторов основного потока, напряжений и токов двигателя в статике. Во время работы двигателя все векторы вращаются в плоскости поперечного сечения вокруг оси вращения ротора, при этом их модули и фазовые сдвиги изменяются.
В этом расчёте производится построение диаграммы для фазы А двигателя в установившемся режиме (длины и фазы векторов не изменяются). Модули и фазы векторов рассчитываются исходя из схемы замещения, рассчитываемой в примере по паспортным данным двигателя МТК011-6 краново-металлургического назначения.
Расчёт двигателя
Определим исходные данные исходя из паспортных данные рассматриваемого АДКЗ:
# Паспортные данные двигателя МТК011-6
Pₙ = 1400; Uₙ = 380; f₁ = 50; # Номинальная мощность [Вт], линейное напряжение [В], частота [В]
nₙ = 870; p = 3; η = 0.72; # Номинальная частота вращения [об/мин], число пар полюсов, КПД
cosϕ = 0.69; Iₙ = 4.8; I₀ = 3.2; # Номинальный коэффициент мощности, номинальный ток [А], ток холостого хода [А]
ki = 3; mₚ = 2.8; mₘ = 2.8; J = 0.02; # Коэффициенты максимального тока, пускового и максимального момента, момент инерции двигателя [кг·м²]
Теперь перейдём к расчёту параметров схемы замещения АДКЗ:
# Расчёт параметров схемы замещения
U₁ = Uₙ/sqrt(3); # Номинальное фазное напряжение статора [В]
n₀ = 60*f₁/p; # Синхронная частота вращения [об/мин]
sₙ = (n₀-nₙ)/n₀; sₖ = sₙ*(mₘ+sqrt(mₘ^2-1)); # Номинальное и критическое скольжение
ω₀ = 2π*f₁/p; ωₙ = π*nₙ/30; # Синхронная и номинальная углова скорость ротора [рад/с]
Mₙ = Pₙ/ωₙ; Mₘ = Mₙ*mₘ; Mₚ = Mₙ*mₚ; # Номинальный, максимальный и пусковой момент [Н·м]
pₘ = 0.05*Pₙ; # Механические потери (5% от Pₙ) [Вт]
C = 0.8093072740472634; # Конструктивный коэффициент (предварительный)
R₂ = 1/3*(Pₙ+pₘ)/(Iₙ^2*(1-sₙ)/sₙ); # Приведённое активное сопротивление роторной обмотки [Ом]
R₁ = U₁*cosϕ*(1-η)/Iₙ - C^2*R₂ - pₘ/(3*Iₙ^2); # Активное сопротивление статорной обмотки [Ом]
L₁σ = L₂σ = U₁/(4π*f₁*(1+C^2)*ki*Iₙ); # Индуктивности рассеивания статора и приведённое ротора [Гн]
L₁ = L₂ = U₁/(2π*f₁*Iₙ*sqrt(1-cosϕ^2)-2/3*(2π*f₁*Mₘ*sₙ)/(p*U₁*sₖ)); # Индуктивности статора и приведённое ротора [Гн]
Lm = L₁ - L₁σ; # Индуктивность магнитной цепи [Гн]
C = 1 + L₁σ/Lm # Конструктивный коэффициент (уточнённый)
X₁σ = 2π*f₁*L₁σ; X₂σ = 2π*f₁*L₂σ # Реактивные сопротивления рассеивания статора и приведённое ротора [Ом]
I₂ = U₁/hypot(R₁+R₂*(1+(1-sₙ)/sₙ), X₁σ+X₂σ) # Ток ротора [А] (предварительное значение)
ψ₂ = atan(X₂σ*sₙ/R₂); # Угол запаздывания тока ротора [рад] (к эдс ротора, предварительное значение)
Для дальнейших расчётов и построения перейдём к комплексному представлению токов и напряжений. Предварительно необходимо определить вспомогательные функции.
Вспомогательные функции
Следующая функция позволяет лаконично подготовить в дальнейшем область построения векторной диаграммы.
"""
coordinateplane(заголовок::String, длина_оси)
Функция для построения координатный осей.
Plots, бэкенд GR.
Получает значение атрибута title и длину оси (X или Y)
Масштаб осей одинаков, подписи графиков - вверху слева
"""
function coordinateplane(заголовок::String, длина_оси)
gr()
plot(size=(500, 500), legend=:topleft, aspect_ratio=:equal,
xlabel="Ось X", ylabel="Ось Y",
title=заголовок, showaxis = false)
quiver!([-длина_оси/2], [0], quiver=([длина_оси], [0]), color=:grey, width = 2) # Ось X
quiver!([0], [-длина_оси/2], quiver=([0], [длина_оси]), color=:grey, width = 2) # Ось Y
end;
Следующая функция совмещает инструкции для предобработки комплексных векторов - масштабирования и поворота, а также построения комплексного вектора относительно предыдущего.
"""
vectorplot(начальный::ComplexF64, результирующий::ComplexF64,
цвет::Symbol=:black, лэйбл::String="")
Функция для построения результирующего вектора, исходящего из начального.
Plots, бэкенд GR.
Получает комплексные значения начального и результирующего векторов, атрибуты color и label результирующего.
Атрибуты поворот и множитель используются для вращения результирующего вектора на заданный угол [рад] и масштабирования соответственно.
Перед использованием рекомендуется выполнить coordinateplane().
"""
function vectorplot(начальный::ComplexF64, результирующий::ComplexF64, цвет::Symbol=:black, лэйбл::String="", поворот=0.0, множитель=1.0)
начальный = начальный*множитель*exp(поворот*im) # Поворот и масштабирование
результирующий = результирующий*множитель*exp(поворот*im) # Поворот и масштабирование
Plots.quiver!([real(начальный)], [imag(начальный)], quiver=([real(результирующий)], [imag(результирующий)]), color=цвет, label=лэйбл)
end;
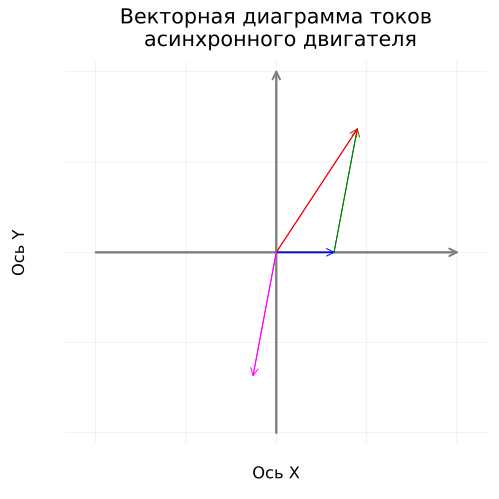
Построение векторной диаграммы токов
Определим комплексные вектора токов:
Ȯ = 0.0 + 0.0*im # Нуль-вектор в начале координат
İ₀ = I₀ + 0.0*im # Комплексный ток холостого хода. Активная составляющая принимается равной 0.0 [A]
İ₂ = I₂*exp((3π/2-ψ₂)*im) # Комплексный ток ротора [A]
İ₁ = İ₀ - İ₂; # Комплексный ток статора [A]
Построим векторную диаграмму токов:
coordinateplane("Векторная диаграмма токов\n асинхронного двигателя", 20)
vectorplot(Ȯ, İ₀, :blue, "İ₀, [A]")
vectorplot(İ₀, -İ₂, :green, "-İ₂, [A]")
vectorplot(Ȯ, İ₁, :red, "İ₁, [A]")
vectorplot(Ȯ, İ₂, :magenta, "İ₂, [A]")
Общий вид диаграммы, а также расположение векторов относительного друг друга и на плоскости соответствуют ожиданиям. Перейдём к уточнению параметров векторов и построению векторной диаграммы напряжений.
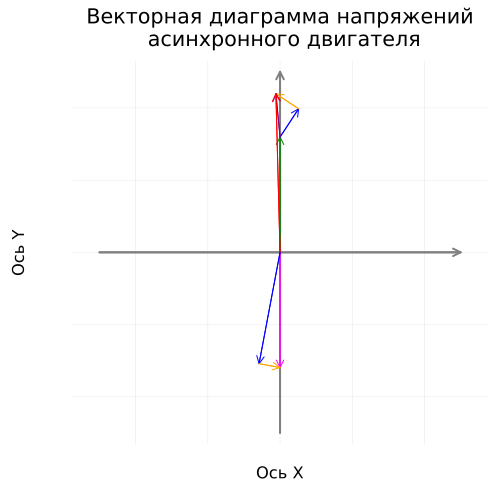
Построение векторной диаграммы напряжений
Определим комплексные вектора напряжений и эдс:
Ż₁ = R₁ + X₁σ*im # Полное комплексное сопротивление цепи статора [В]
Ů₁_r = İ₁*R₁ # Активное падение напряжения в цепи статора [В]
Ů₁_x = İ₁*X₁σ*im # Реактивное падение напряжения в цепи статора [В]
Ů₁_z = İ₁*Ż₁ # Полное падение напряжения в цепи статора [В]
Ů₁ = U₁*im # Комплексное напряжение питания [В]
Ė₁ = Ė₂ = Ů₁_z - Ů₁; # Эдс статора и приведённая ротора [В]
Уточним расположение на плоскости и параметры комплексных векторов:
Ė₁ = Ė₂ = abs(Ė₁)*exp(-π/2*im) # Эдс статора и приведённая ротора [В] (отложено вдоль комплексной оси)
Ů₁ = -Ė₁ + Ů₁_z # Напряжение питания [В] (с учётом поворота вектора эдс)
I₂ = abs(Ė₂)/hypot((R₂/sₙ), X₂σ) # Приведённый модуль тока ротора [А] (уточнённое значение)
ψ₂ = atan(X₂σ*sₙ/R₂) # Угол запаздывания тока ротора [рад] (уточнённое значение)
İ₂ = I₂*exp((3π/2-ψ₂)*im) # Приведённый комплексный ток ротора [А]
İ₁ = İ₀ - İ₂ # Комплексный ток статора [A] (уточнённый)
Ů₂_r = İ₂*(R₂ + R₂*(1-sₙ)/sₙ) # Приведённое активное падение напряжения в цепи ротора [В]
Ů₂_x = İ₂*X₂σ*im; # Приведённое реактивное падение напряжения в цепи ротора [В]
Построим векторную диаграмму напряжений АДКЗ:
coordinateplane("Векторная диаграмма напряжений\n асинхронного двигателя", 500)
vectorplot(Ȯ, -Ė₁, :green, "-Ė₁, [В]")
vectorplot(-Ė₁, Ů₁_r, :blue, "Ů₁_r, [В]")
vectorplot(-Ė₁+Ů₁_r, Ů₁_x, :orange, "Ů₁_x, [В]")
vectorplot(-Ė₁, Ů₁_z, :purple, "Ů₁_z, [В]")
vectorplot(Ȯ, Ů₁, :red, "Ů₁, [В]")
vectorplot(Ȯ, Ė₁, :magenta, "Ė₁, [В]")
vectorplot(Ȯ, Ů₂_r, :blue, "Ů₂_r, [В]")
vectorplot(Ů₂_r, Ů₂_x, :orange, "Ů₂_x, [В]")
Диаграмма напряжений также соответствует ожидаемым параметрам. В завершение построим полную диаграмму токов и напряжений, вращающуюся в комплексной плоскости.
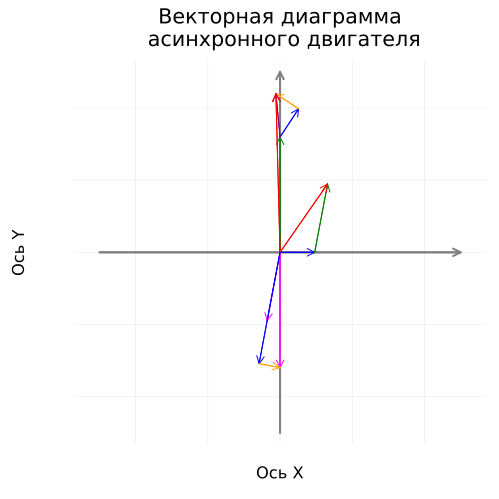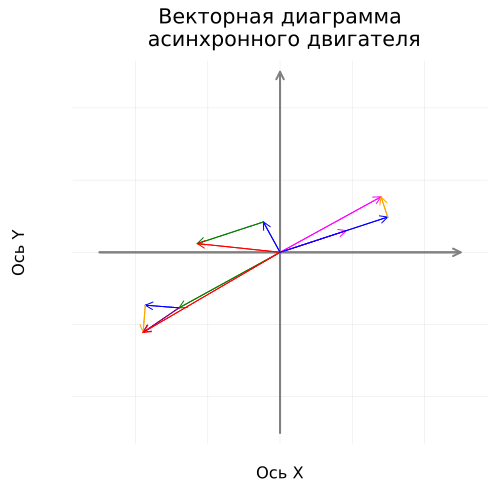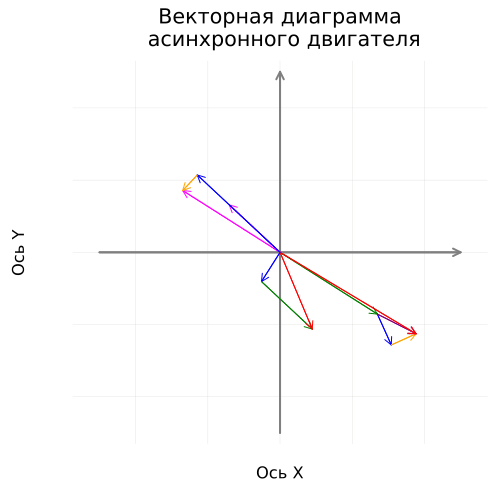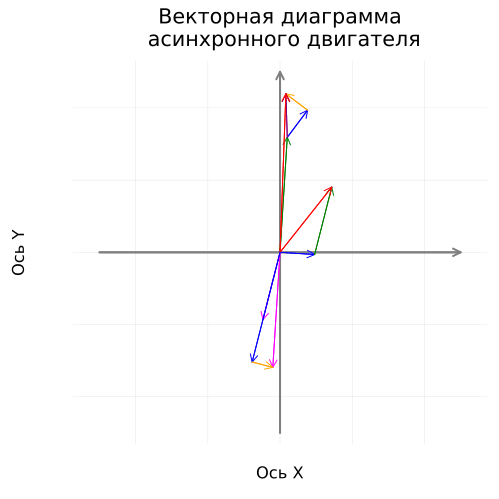
Построение вращающейся векторной диаграммы
Зададим цикл вращения, который будет анимирован.
Вектора тока отмасштабируем для наглядности.
RotateDiagram = @animate for δ in range(0.0, step=2π/100, length = 100)
coordinateplane("Векторная диаграмма\n асинхронного двигателя", 500)
vectorplot(Ȯ, İ₀, :blue, "İ₀·15, [A]", δ, 15)
vectorplot(İ₀, -İ₂, :green, "-İ₂·15, [A]", δ, 15)
vectorplot(Ȯ, İ₁, :red, "İ₁·15, [A]", δ, 15)
vectorplot(Ȯ, İ₂, :magenta, "İ₂·15, [A]", δ, 15)
vectorplot(Ȯ, -Ė₁, :green, "-Ė₁, [В]", δ)
vectorplot(-Ė₁, Ů₁_r, :blue, "Ů₁_r, [В]", δ)
vectorplot((-Ė₁+Ů₁_r), Ů₁_x, :orange, "Ů₁_x, [В]", δ)
vectorplot(-Ė₁, Ů₁_z, :purple, "Ů₁_z, [В]", δ)
vectorplot(Ȯ, Ů₁, :red, "Ů₁, [В]", δ)
vectorplot(Ȯ, Ė₁, :magenta, "Ė₁, [В]", δ)
vectorplot(Ȯ, Ů₂_r, :blue, "Ů₂_r, [В]", δ)
vectorplot(Ů₂_r, Ů₂_x, :orange, "Ů₂_x, [В]", δ)
end
gif(RotateDiagram, "RotateDiagram.gif", fps = 20)
Следует заметить, что частота вращения векторов в диаграмме снижена для возможности анализа вращения в 250 раз (с 50 до 1/5 Гц).
Заключение
В результате работы скрипта мы получили вращающуюся векторную диаграмму токов и напряжений АДКЗ, вращающуюся в комплексной плоскости. Дальнейшие возможные продолжения этого примера - уточнение расчёта схемы замещения и векторов, построение диаграммы в динамическом режиме (регулирование нагрузки, разгон или торможение), построение диаграммы для трёх фаз - симметричных и несимметричных.
Список использованной литературы
- Вольдек А.И. Электрические машины. Учебник для студентов высш. техн. заведений. - 3-е изд., перераб. - Л.: Энергия, 1978. - 832 с., ил.
- Вешеневский С.Н. Характеристики двигателей в электроприводе - 6-е изд., испр. - М.: Энергия, 1977. - 431 с., ил.