Общее руководство по DynamicalSystems.jl

На этой странице приводятся краткие, но конкретные вводные сведения о библиотеке DynamicalSystems.jl. Здесь описываются основные компоненты и то, как они формируют интерфейс, используемый остальными частями библиотеки. Вы также найдете несколько примеров использования, позволяющих связать воедино различные пакеты библиотеки.

Выполнение приведенных в этом руководстве действий займет у вас около 20 минут.

Основные компоненты

Отдельные пакеты, составляющие DynamicalSystems, отлично взаимодействуют друг с другом благодаря следующим двум компонентам.

StateSpaceSet, представляющий числовые данные. Это могут быть наблюдения или измерения в экспериментах, выборочные траектории динамических систем или просто неупорядоченные наборы в пространстве состояний. StateSpaceSet — это контейнер с одинаковыми по размеру точками, представляющими многомерные временные ряды или многомерные наборы данных. Временные ряды, которые являются одномерными наборами, представлены базовым типом Julia AbstractVector{<:Real}.
DynamicalSystem, который является абстрактным представлением динамической системы с известным правилом динамической эволюции. DynamicalSystem определяет расширяемый интерфейс, но обычно используются конкретные реализации, такие как DeterministicIteratedMap или CoupledODEs.

Создание динамических систем

В большинстве случаев для создания динамической системы необходимы три вещи.

Динамическое правило f: функция Julia, которая предоставляет инструкции по эволюции динамической системы во времени.
Состояние u: массивоподобный контейнер, содержащий переменные динамической системы, а также определяющий начальное состояние системы.
Параметры p: произвольный контейнер, который параметризует f.

Для большинства конкретных реализаций DynamicalSystem существует два способа определения f, u. Различие в том, определяется ли f как функция на месте (iip) или не на месте (oop).

oop: f должна иметь вид f(u, p, t) -> out , что означает, что при заданном состоянии u::SVector{<:Real} и некотором контейнере параметров p она возвращает выходные данные f в виде SVector{<:Real} (статического вектора).
iip: f должна иметь вид f!(out, u, p, t) , что означает, что при заданном состоянии u::AbstractArray{<:Real} и некотором контейнере параметров p она на месте записывает выходные данные f в out::AbstractArray{<:Real}. Функция должна возвращать nothing в качестве окончательного оператора.

t означает текущее время в обоих случаях. iip предлагается для систем с большой размерностью, а oop — для систем с малой. Точка равновесия находится в диапазоне от 10 до 100 измерений, но ее следует проверять в каждом конкретном случае, поскольку она зависит от сложности f.

Пример: отображение Эно

Создадим отображение Эно, определяемое как

с параметрами .

Сначала определим динамическое правило как стандартную функцию Julia. Поскольку динамическая система только двумерная, мы должны использовать форму не на месте, которая возвращает SVector со следующим состоянием:

using DynamicalSystems

function henon_rule(u, p, n) # здесь `n` — это «время», но мы его не используем.
    x, y = u # состояние системы
    a, b = p # параметры системы
    xn = 1.0 - a*x^2 + y
    yn = b*x
    return SVector(xn, yn)
end

henon_rule (generic function with 1 method)

Затем определим начальное состояние и параметры

u0 = [0.2, 0.3]
p0 = [1.4, 0.3]

2-element Vector{Float64}:
 1.4
 0.3

И, наконец, передаем эти три компонента в DeterministicIteratedMap:

henon = DeterministicIteratedMap(henon_rule, u0, p0)

2-dimensional DeterministicIteratedMap
 deterministic: true
 discrete time: true
 in-place:      false
 dynamic rule:  henon_rule
 parameters:    [1.4, 0.3]
 time:          0
 state:         [0.2, 0.3]

henon представляет собой DynamicalSystem, одну из двух основных структур библиотеки. Они могут развиваться в интерактивном режиме и запрашиваться с помощью интерфейса, определенного DynamicalSystem. Самое простое, что можно сделать с DynamicalSystem, — это получить ее траекторию:

total_time = 10_000
X, t = trajectory(henon, total_time)

(2-dimensional StateSpaceSet{Float64} with 10001 points, 0:1:10000)

2-dimensional StateSpaceSet{Float64} with 10001 points
  0.2        0.3
  1.244      0.06
 -1.10655    0.3732
 -0.341035  -0.331965
  0.505208  -0.102311
  0.540361   0.151562
  0.742777   0.162108
  0.389703   0.222833
  1.01022    0.116911
 -0.311842   0.303065
  ⋮
 -0.582534   0.328346
  0.853262  -0.17476
 -0.194038   0.255978
  1.20327   -0.0582113
 -1.08521    0.36098
 -0.287758  -0.325562
  0.558512  -0.0863275
  0.476963   0.167554
  0.849062   0.143089

X представляет собой StateSpaceSet, вторую из основных структур библиотеки. Ниже мы рассмотрим, как и где использовать StateSpaceset, а пока давайте просто построим график рассеяния

using CairoMakie
scatter(X[:, 1], X[:, 2])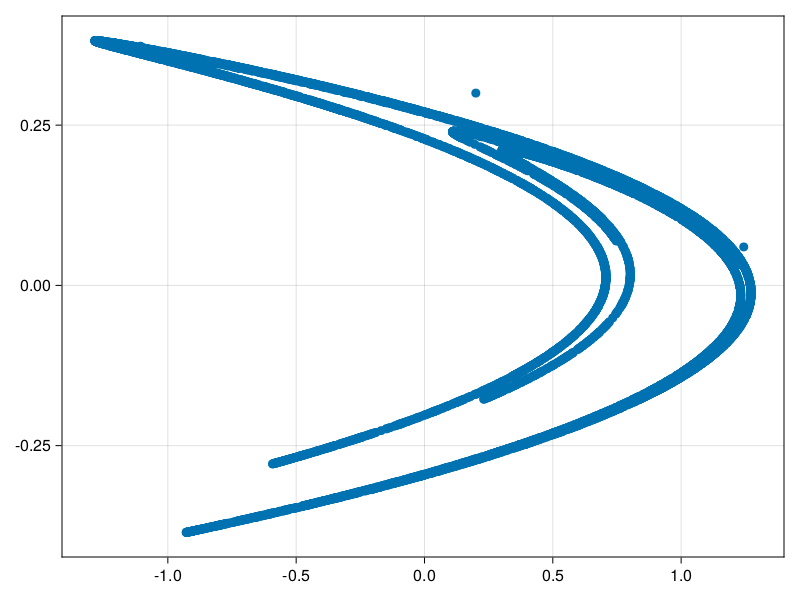

Пример: модель Лоренца 96

Давайте создадим еще одну динамическую систему — модель Лоренца 96:

для и .

Здесь вместо отображения дискретного времени мы имеем связанных обыкновенных дифференциальных уравнений. Однако создание динамической системы происходит точно так же, как и выше, но с использованием CoupledODEs вместо DeterministicIteratedMap.

Сначала создадим функцию динамического правила. Поскольку эта динамическая система может быть произвольно высокоразмерной, лучше использовать форму на месте для f, перезаписывая на месте скорость изменения в заранее выделенном контейнере. К именам функций, изменяющих свои аргументы на месте, принято добавлять символ (!).

function lorenz96_rule!(du, u, p, t)
    F = p[1]; N = length(u)
    # 3 пограничных случая
    du[1] = (u[2] - u[N - 1]) * u[N] - u[1] + F
    du[2] = (u[3] - u[N]) * u[1] - u[2] + F
    du[N] = (u[1] - u[N - 2]) * u[N - 1] - u[N] + F
    # тогда общий случай
    for n in 3:(N - 1)
        du[n] = (u[n + 1] - u[n - 2]) * u[n - 1] - u[n] + F
    end
    return nothing # всегда `return nothing` для формы на месте!
end

lorenz96_rule! (generic function with 1 method)

затем, как и раньше, мы определяем начальное состояние и параметры и инициализируем систему

N = 6
u0 = range(0.1, 1; length = N)
p0 = [8.0]
lorenz96 = CoupledODEs(lorenz96_rule!, u0, p0)

6-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      true
 dynamic rule:  lorenz96_rule!
 ODE solver:    Tsit5
 ODE kwargs:    (abstol = 1.0e-6, reltol = 1.0e-6)
 parameters:    [8.0]
 time:          0.0
 state:         [0.1, 0.28, 0.46, 0.64, 0.82, 1.0]

и, как и раньше, мы можем получить траекторию тем же способом

total_time = 12.5
sampling_time = 0.02
Y, t = trajectory(lorenz96, total_time; Ttr = 2.2, Δt = sampling_time)
Y

6-dimensional StateSpaceSet{Float64} with 626 points
  3.15368   -4.40493  0.0311581  0.486735  1.89895   4.15167
  2.71382   -4.39303  0.395019   0.66327   2.0652    4.32045
  2.25088   -4.33682  0.693967   0.879701  2.2412    4.46619
  1.7707    -4.24045  0.924523   1.12771   2.42882   4.58259
  1.27983   -4.1073   1.08656    1.39809   2.62943   4.66318
  0.785433  -3.94005  1.18319    1.6815    2.84384   4.70147
  0.295361  -3.74095  1.2205     1.96908   3.07224   4.69114
 -0.181932  -3.51222  1.20719    2.25296   3.3139    4.62628
 -0.637491  -3.25665  1.154      2.5267    3.56698   4.50178
 -1.06206   -2.9781   1.07303    2.7856    3.82827   4.31366
  ⋮                                                  ⋮
  3.17245    2.3759   3.01796    7.27415   7.26007  -0.116002
  3.29671    2.71146  3.32758    7.5693    6.75971  -0.537853
  3.44096    3.09855  3.66908    7.82351   6.13876  -0.922775
  3.58387    3.53999  4.04452    8.01418   5.39898  -1.25074
  3.70359    4.03513  4.45448    8.1137    4.55005  -1.5042
  3.78135    4.57879  4.89677    8.09013   3.61125  -1.66943
  3.80523    5.16112  5.36441    7.90891   2.61262  -1.73822
  3.77305    5.7684   5.84318    7.53627   1.59529  -1.71018
  3.6934     6.38507  6.30923    6.94454   0.61023  -1.59518

Мы не можем построить 6-мерный график, но можем визуализировать все временные ряды.

fig = Figure()
ax = Axis(fig[1, 1]; xlabel = "time", ylabel = "variable")
for var in columns(Y)
    lines!(ax, t, var)
end
fig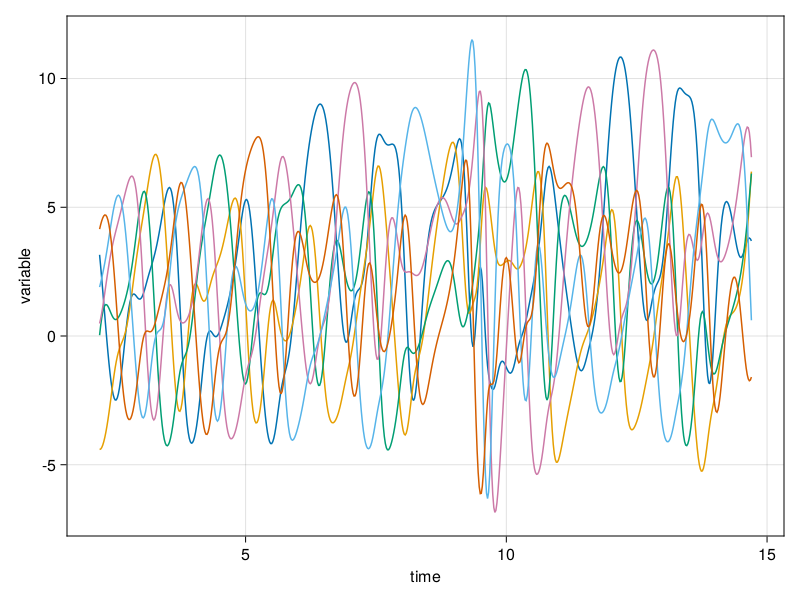

Решение ODE

Динамические системы с непрерывным временем развиваются с помощью DifferentialEquations.jl. При инициализации CoupledODEs вы можете настроить свойства решателя по своему усмотрению, используя любой из решателей ODE и любой из обычных параметров решателя. Например:

using OrdinaryDiffEq # доступ к решателям ODE
diffeq = (alg = Vern9(), abstol = 1e-9, reltol = 1e-9)
lorenz96_vern = ContinuousDynamicalSystem(lorenz96_rule!, u0, p0; diffeq)

6-dimensional CoupledODEs
 deterministic: true
 discrete time: false
 in-place:      true
 dynamic rule:  lorenz96_rule!
 ODE solver:    Vern9
 ODE kwargs:    (abstol = 1.0e-9, reltol = 1.0e-9)
 parameters:    [8.0]
 time:          0.0
 state:         [0.1, 0.28, 0.46, 0.64, 0.82, 1.0]

Y, t = trajectory(lorenz96_vern, total_time; Ttr = 2.2, Δt = sampling_time)
Y[end]

6-element SVector{6, Float64} with indices SOneTo(6):
  3.8390248122550252
  6.1557095311542325
  6.080625689025621
  7.278588308988913
  1.2582152212831657
 -1.5297062916833186

Использование динамических систем

Вы можете использовать интерфейс DynamicalSystem для разработки алгоритмов, использующих динамические системы с известным правилом эволюции. Это можно сделать с помощью двух основных пакетов библиотеки — ChaosTools и Attractors. Например, может потребоваться вычислить спектр Ляпунова системы Лоренца 96, описанной выше. Это так же просто, как вызвать функцию lyapunovspectrum с помощью lorenz96.

steps = 10_000
lyapunovspectrum(lorenz96, steps)

6-element Vector{Float64}:
  0.9578297436475178
  0.0007190960151481466
 -0.15749134695138844
 -0.7575338861926539
 -1.4036253850302072
 -4.639894729260599

Как и ожидалось, существует по крайней мере одна положительная экспонента Ляпунова (до того, как система станет хаотической) и по крайней мере одна нулевая экспонента Ляпунова, поскольку система является непрерывной по времени.

Или же нужно оценить области притяжения мультиустойчивой динамической системы. Отображение Эно является мультиустойчивой в том смысле, что некоторые начальные условия расходятся до бесконечности, а другие сходятся к хаотическому аттрактору. Вычислить эти области притяжения очень просто с помощью Attractors, и это будет выглядеть следующим образом:

# определим сетку пространства состояний для вычисления областей:
xg = yg = range(-2, 2; length = 201)
# найдем аттракторы с помощью рекурсий в пространстве состояний:
mapper = AttractorsViaRecurrences(henon, (xg, yg); sparse = false)
# вычислим полные области притяжения:
basins, attractors = basins_of_attraction(mapper; show_progress = false)

(Int32[-1 -1 … -1 -1; -1 -1 … -1 -1; … ; -1 -1 … -1 -1; -1 -1 … -1 -1], Dict{Int32, StateSpaceSet{2, Float64}}(1 => 2-dimensional StateSpaceSet{Float64} with 511 points))

fig, ax = heatmap(xg, yg, basins)
x, y = columns(X) # аттрактор отображения Эно
scatter!(ax, x, y; color = "black")
fig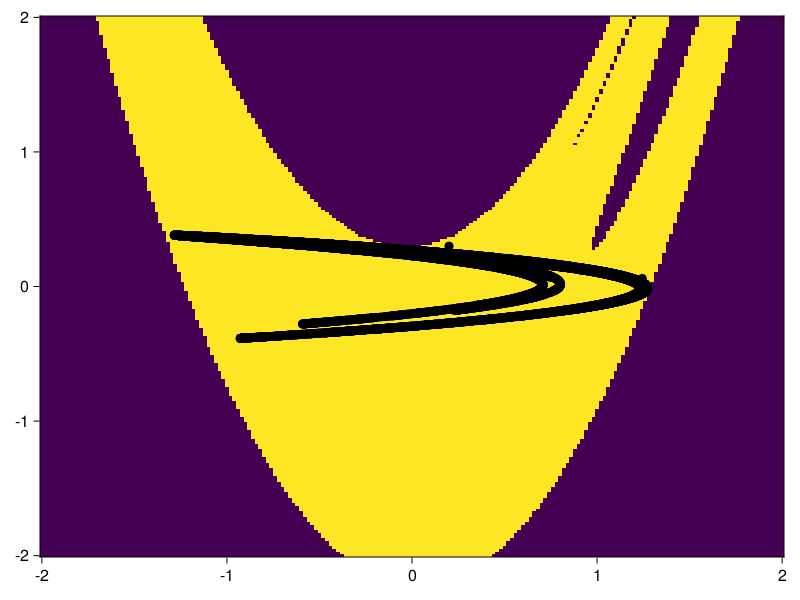

Вы также можете использовать экземпляр DynamicalSystem непосредственно для создания собственного алгоритма, если он еще не реализован (а затем позже предоставить его для реализации ;)). Динамическая система может быть эволюционирована вперед во времени с помощью step!:

henon

2-dimensional DeterministicIteratedMap
 deterministic: true
 discrete time: true
 in-place:      false
 dynamic rule:  henon_rule
 parameters:    [1.4, 0.3]
 time:          5
 state:         [-1.5266434026801804e8, -3132.7519146699206]

Обратите внимание, что время не равно 0, потому что henon уже прошло вперед, когда мы вызвали с его помощью функцию basins_of_attraction. Мы можем продвинуть его еще дальше:

step!(henon)

2-dimensional DeterministicIteratedMap
 deterministic: true
 discrete time: true
 in-place:      false
 dynamic rule:  henon_rule
 parameters:    [1.4, 0.3]
 time:          6
 state:         [-3.262896110526e16, -4.579930208040541e7]

step!(henon, 2)

2-dimensional DeterministicIteratedMap
 deterministic: true
 discrete time: true
 in-place:      false
 dynamic rule:  henon_rule
 parameters:    [1.4, 0.3]
 time:          8
 state:         [-3.110262842032839e66, -4.4715262317959936e32]

Дополнительные сведения о прямом использовании экземпляров DynamicalSystem см. в документации по DynamicalSystemsBase.

Наборы пространств состояний

Напомним, что выводом функции trajectory является StateSpaceSet:

2-dimensional StateSpaceSet{Float64} with 10001 points
  0.2        0.3
  1.244      0.06
 -1.10655    0.3732
 -0.341035  -0.331965
  0.505208  -0.102311
  0.540361   0.151562
  0.742777   0.162108
  0.389703   0.222833
  1.01022    0.116911
 -0.311842   0.303065
  ⋮
 -0.582534   0.328346
  0.853262  -0.17476
 -0.194038   0.255978
  1.20327   -0.0582113
 -1.08521    0.36098
 -0.287758  -0.325562
  0.558512  -0.0863275
  0.476963   0.167554
  0.849062   0.143089

Он выводится в виде матрицы, где каждый столбец — это временной ряд каждой динамической переменной. В действительности это вектор векторов статического размера (по соображениям производительности). При индексировании с одним индексом он ведет себя как вектор векторов

X[1]

2-element SVector{2, Float64} with indices SOneTo(2):
 0.2
 0.3

X[2:5]

2-dimensional StateSpaceSet{Float64} with 4 points
  1.244      0.06
 -1.10655    0.3732
 -0.341035  -0.331965
  0.505208  -0.102311

При индексировании с двумя индексами он ведет себя как матрица

X[2:5, 2]

4-element Vector{Float64}:
  0.06
  0.3732
 -0.3319651199999999
 -0.10231059085086688

При итерации он итерируется по содержащимся точкам

for (i, point) in enumerate(X)
    @show point
    i > 5 && break
end

point = [0.2, 0.3]
point = [1.244, 0.06]
point = [-1.1065503999999997, 0.3732]
point = [-0.34103530283622296, -0.3319651199999999]
point = [0.5052077711071681, -0.10231059085086688]
point = [0.5403605603672313, 0.1515623313321504]

map(point -> point[1] + point[2], X)

10001-element Vector{Float64}:
  0.5
  1.304
 -0.7333503999999997
 -0.6730004228362229
  0.40289718025630117
  0.6919228916993818
  0.9048851501617762
  0.6125365596336813
  1.1271278272148746
 -0.008777065619615998
  ⋮
 -0.2541879392427324
  0.678501271515278
  0.061940665344374896
  1.145056192451011
 -0.7242249528790483
 -0.6133198017049188
  0.47218423998951875
  0.6445165778497133
  0.9921511619004666

Столбцы набора можно получить с помощью вспомогательной функции columns.

x, y = columns(X)
summary.((x, y))

("10001-element Vector{Float64}", "10001-element Vector{Float64}")

Использование наборов пространств состояний

Несколько пакетов библиотеки работают с StateSpaceSets.

Вы можете использовать ComplexityMeasures для получения энтропии или других показателей сложности заданного набора. Ниже мы получим энтропию естественной плотности хаотического аттрактора путем разбиения на гистограмму, состоящую примерно из 50 столбцов на измерение:

prob_est = ValueHistogram(50)
entropy(prob_est, X)

7.825799208736613

В качестве альтернативы можно использовать FractalDimensions для получения фрактальных измерений хаотического аттрактора отображения Эно с помощью алгоритма Грассбергера-Прокаччиа:

grassberger_proccacia_dim(X)

1.2232922815092426

Или можно получить рекуррентную матрицу набора пространств состояний с помощью RecurrenceAnalysis.

R = RecurrenceMatrix(Y, 8.0)
Rg = grayscale(R)
rr = recurrencerate(R)
heatmap(Rg; colormap = :grays,
    axis = (title = "recurrence rate = $(rr)", aspect = 1,)
)

Нелинейный анализ дополнительных временных рядов

Одним из способов получения набора StateSpaceSet является траектория (trajectory) известной динамической системы. Однако существует еще один вариант — внедрение координат задержки в измеряемый или наблюдаемый временной ряд. Например, можно использовать optimal_separated_de из модуля DelayEmbeddings, чтобы создать оптимизированное внедрение координат задержки временного ряда

w = Y[:, 1] # первая переменная Лоренца 96
𝒟, τ, e = optimal_separated_de(w)
𝒟

5-dimensional StateSpaceSet{Float64} with 558 points
  3.15369   -2.40036    1.60497   2.90499  5.72572
  2.71384   -2.24811    1.55832   3.04987  5.6022
  2.2509    -2.02902    1.50499   3.20633  5.38629
  1.77073   -1.75077    1.45921   3.37699  5.07029
  1.27986   -1.42354    1.43338   3.56316  4.65003
  0.785468  -1.05974    1.43672   3.76473  4.12617
  0.295399  -0.673567   1.47423   3.98019  3.50532
 -0.181891  -0.280351   1.54635   4.20677  2.80048
 -0.637447   0.104361   1.64932   4.44054  2.03084
 -1.06201    0.465767   1.77622   4.67654  1.22067
  ⋮
  7.42111    9.27879   -1.23936   5.15945  3.25618
  7.94615    9.22663   -1.64222   5.24344  3.34749
  8.40503    9.13776   -1.81947   5.26339  3.46932
  8.78703    8.99491   -1.77254   5.22631  3.60343
  9.08701    8.77963   -1.51823   5.13887  3.72926
  9.30562    8.47357   -1.08603   5.00759  3.82705
  9.4488     8.06029   -0.514333  4.83928  3.88137
  9.52679    7.52731    0.153637  4.6414   3.88458
  9.55278    6.86845    0.873855  4.42248  3.83902

и сравнить

fig = Figure()
axs = [Axis3(fig[1, i]) for i in 1:2]
for (S, ax) in zip((Y, 𝒟), axs)
    lines!(ax, S[:, 1], S[:, 2], S[:, 3])
end
fig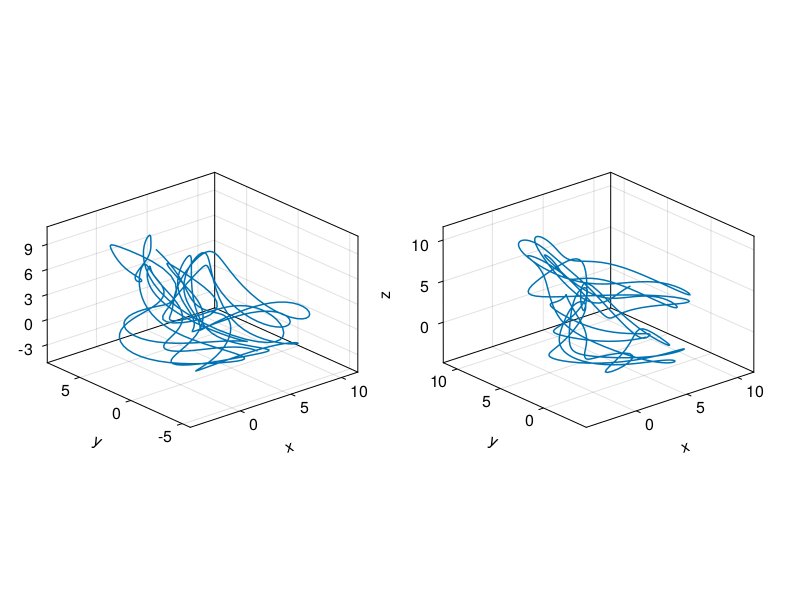

Поскольку 𝒟 — это просто другой набор пространства состояний, можно с тем же успехом использовать для него любой из описанных выше конвейеров анализа.

Последний пакет, о котором стоит упомянуть, — TimeseriesSurrogates, который связан со всеми остальными средствами анализа наблюдаемых или измеряемых данных, предоставляя основу для проверки достоверности или гипотез. Например, если у нас есть измеряемый временной ряд, но мы не уверены, представляет ли он детерминированную систему со структурой в пространстве состояний или большей частью шум, мы можем провести суррогатный тест. Для этого мы используем surrogenerator и RandomFourier из модуля TimeseriesSurrogates, а также generalized_dim из модуля FractalDimensions (потому что он лучше работает в наборах с шумами).

x = X[:, 1] # временные ряды отображения Эно
# загрязняем шумом
using Random: Xoshiro
rng = Xoshiro(1234)
x .+= randn(rng, length(x))/100
# вычисляем загрязненную шумами фрактальную размерность.
Δ_orig = generalized_dim(embed(x, 2, 1))

1.3801073957979793

Проводим суррогатный тест

surrogate_method = RandomFourier()
sgen = surrogenerator(x, surrogate_method, rng)

Δ_surr = map(1:1000) do i
    s = sgen()
    generalized_dim(embed(s, 2, 1))
end

1000-element Vector{Float64}:
 1.8297218640747606
 1.8449246422083758
 1.827998413768852
 1.8301078704767055
 1.810704251592814
 1.8324978359365702
 1.8300954188512213
 1.8416570396197014
 1.8575804541517287
 1.821435647618282
 ⋮
 1.8768262063118628
 1.8287938131103985
 1.8435474417451545
 1.8129026565561648
 1.8551700924676993
 1.8283378225272842
 1.8211346475312316
 1.8369834750866052
 1.8368699339310082

и визуализируем его результат.

fig, ax = hist(Δ_surr)
vlines!(ax, Δ_orig)
fig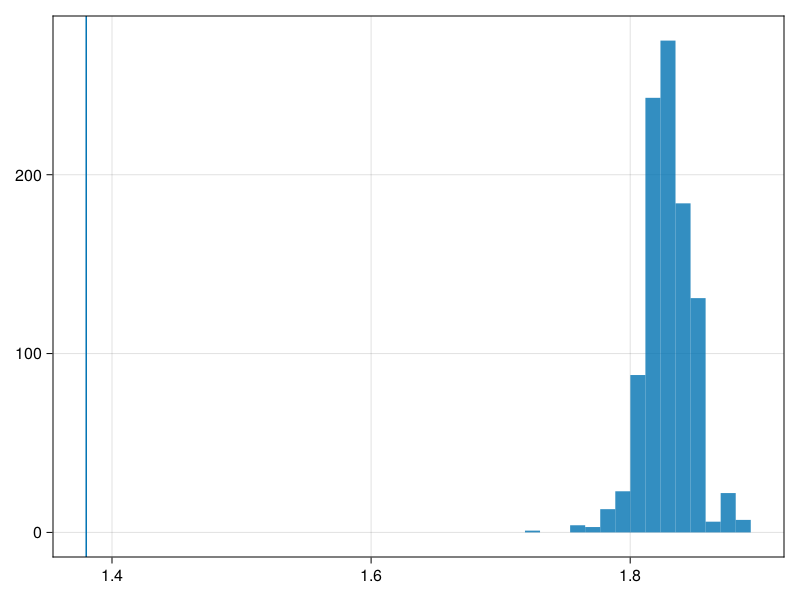

Поскольку реальное значение находится за пределами распределения, есть уверенность, что данные не являются чистым шумом.

Справка по основным компонентам

# StateSpaceSets.StateSpaceSet — Type

StateSpaceSet{D, T} <: AbstractStateSpaceSet{D,T}

Выделенный интерфейс для наборов в пространстве состояний. Это упорядоченный контейнер одинаковых по размеру точек длиной D. Каждая точка представлена вектором SVector{D, T}. Данные являются стандартным вектором Vector{SVector} Julia и могут быть получены с помощью vec(ssset::StateSpaceSet). Обычно порядок точек в наборе соответствует направлению времени, но это не обязательно так.

При индексировании с одним индексом StateSpaceSet ведет себя как вектор точек. При индексировании с двумя индексами он ведет себя как матрица, каждый из столбцов которой является временным рядом каждой переменной. При итерации он итерируется по содержащимся точкам. Подробные сведения см. в описании индексирования ниже.

StateSpaceSet также поддерживает почти все целесообразные векторные операции, такие как append!, push!, hcat, eachrow, помимо прочих.

Описание индексирования

Далее пусть i, j являются целыми числами, typeof(X) <: AbstractStateSpaceSet и v1, v2 являются <: AbstractVector{Int} (v1, v2 также могут быть диапазонами, а для повышения производительности v2 будет SVector{Int}).

X[i] == X[i, :] задает i-ю точку (возвращает SVector)
X[v1] == X[v1, :], возвращает StateSpaceSet с точками в этих индексах.
X[:, j] задает j-ю переменную временного ряда (или коллекции) как вектор (Vector)
X[v1, v2], X[:, v2] возвращает StateSpaceSet с соответствующими записями (первые индексы представляют собой индекс времени или точки, вторые — переменные)
значение X[i, j] j-й переменной в i-й точке времени

Для преобразования используйте Matrix(ssset) или StateSpaceSet(matrix). Предполагается, что каждый столбец матрицы (matrix) является одной переменной. Различные векторы временных рядов x, y, z, ... можно передавать в виде StateSpaceSet(x, y, z, ...). Можно использовать columns(dataset) для получения обратных величин, т. е. всех столбцов набора данных в кортеже.

# DynamicalSystemsBase.DynamicalSystem — Type

DynamicalSystem

DynamicalSystem — это абстрактный супертип, охватывающий все конкретные реализации того, что считается «динамической системой» в библиотеке DynamicalSystems.jl.

Все конкретные реализации DynamicalSystem могут итеративно эволюционировать во времени с помощью функции step!. Таким образом, большинство функций библиотеки, которые развивают систему, изменят ее текущее состояние и (или) параметры. Сведения о том, как это влияет на распараллеливание, можно найти в документации в Интернете.

DynamicalSystem далее разделяется на два абстрактных типа: ContinuousTimeDynamicalSystem, DiscreteTimeDynamicalSystem. Простейшими и наиболее распространенными конкретными реализациями DynamicalSystem являются DeterministicIteratedMap или CoupledODEs.

Описание

Документация по DynamicalSystem соответствует содержимому главы 1 книги Nonlinear Dynamics (Нелинейная динамика), авторы: Дацерис (Datseris) и Парлиц (Parlitz), Springer 2022.

ds::DynamicalSystem представляет поток Φ в пространстве состояний. В основном он включает в себя три элемента.

Состояние, обычно обозначаемое как u, с начальным значением u0. Пространство, которое занимает u, — это пространство состояний ds, а длина u — это измерение ds (и пространства состояний).
Динамическое правило, обычно обозначаемое f, которое указывает, как развивается или изменяется состояние со временем при вызове функции step!. f является стандартной функцией Julia; см. ниже.
Контейнер параметров p, который параметризует f. p может быть чем угодно, но в целом рекомендуется, чтобы это был устойчивый по типу изменяемый контейнер.

В общем, любой набор величин, изменяющихся во времени, можно считать динамической системой, однако конкретные подтипы DynamicalSystem гораздо более специфичны в своей области применения. Конкретные подтипы обычно содержат больше информации, чем три вышеперечисленных элемента.

В этой области динамические системы имеют известное динамическое правило f, определяемое как стандартная функция Julia. Наблюдаемые или измеряемые данные из динамической системы представляются с помощью StateSpaceSet и являются конечными. Такие данные получают из функции trajectory или из экспериментального измерения динамической системы с неизвестным динамическим правилом.

Инструкции по созданию f и u

Для большинства конкретных реализаций DynamicalSystem, за исключением ArbitrarySteppable, существует два способа реализации динамического правила f, и, как следствие, они имеют тип состояния u. Различие проводится в зависимости от того, определяется ли f как функция на месте (iip) или не на месте (oop).

oop: f должна иметь вид f(u, p, t) -> out, что означает, что при заданном состоянии u::SVector{<:Real} и некотором контейнере параметров p она возвращает вывод f в виде SVector{<:Real} (статического вектора).
iip: f должна иметь вид f!(out, u, p, t), что означает, что при заданном состоянии u::AbstractArray{<:Real} и некотором контейнере параметров p она на месте записывает выходные данные f в out::AbstractArray{<:Real}. Функция должна возвращать nothing в качестве окончательного оператора.

Независимо от того, является ли динамическая система автономной (f не зависит от времени) или нет, все равно необходимо включать t в качестве аргумента в f. Некоторые алгоритмы используют эту информацию, некоторые — нет, но мы предпочитаем сохранять последовательный интерфейс в любом случае. Вы также можете преобразовать любую систему в автономную, сделав время дополнительной переменной. Если система неавтономна, то ее эффективная размерность равна dimension(ds)+1.

API

API, который использует интерфейс DynamicalSystem, — это функции, перечисленные ниже. Полученный конкретный экземпляр подтипа DynamicalSystem можно запросить или изменить с помощью следующих функций.

Основное использование конкретного экземпляра динамической системы — это предоставление его нижележащим функциям, таким как lyapunovspectrum из ChaosTools.jl или basins_of_attraction из Attractors.jl. Обычный пользователь, скорее всего, не будет напрямую использовать следующий API, а будет применять только при разработке новых реализаций алгоритмов, использующих динамические системы.

API — информация

ds(t) с ds экземпляром DynamicalSystem: возвращает состояние ds в момент времени t. Для систем с непрерывным временем он выполняет интерполяцию и экстраполяцию, а для систем с дискретным временем он работает, только если t является текущим временем.
current_state
initial_state
current_parameters
initial_parameters
isdeterministic
isdiscretetime
dynamic_rule
current_time
initial_time
isinplace
succesful_step

API — изменить состояние

reinit!
set_state!
set_parameter!
set_parameters!

Реализации динамических систем

# DynamicalSystemsBase.DeterministicIteratedMap — Type

DeterministicIteratedMap <: DynamicalSystem
DeterministicIteratedMap(f, u0, p = nothing; t0 = 0)

Детерминированная динамическая система с дискретным временем, определяемая итерированным отображением следующим образом:

Псевдонимом для DeterministicIteratedMap является DiscreteDynamicalSystem.

При необходимости можно настроить контейнер параметров p и начальное время t0.

Инструкции по созданию f, u0 см. в DynamicalSystem.

# DynamicalSystemsBase.CoupledODEs — Type

CoupledODEs <: ContinuousTimeDynamicalSystem
CoupledODEs(f, u0 [, p]; diffeq, t0 = 0.0)

Детерминированная динамическая система с дискретным временем, определяемая набором связанных обыкновенных дифференциальных уравнений следующим образом:

Псевдонимом для CoupledODE является ContinuousDynamicalSystem.

При необходимости можно указать контейнер параметров p и начальное время t0.

Инструкции по созданию f, u0 см. в DynamicalSystem.

Именованные аргументы DifferentialEquations.jl и взаимодействие с ними

Для решения ODE используются решатели DifferentialEquations.jl. При инициализации CoupledODEs можно указать решатель, который будет интегрировать f во времени, также любые другие параметры интегрирования, используя ключевое слово diffeq. Например, можно использовать diffeq = (abstol = 1e-9, reltol = 1e-9). Если вы хотите указать решатель, сделайте это с помощью ключевого слова alg, например: diffeq = (alg = Tsit5(), reltol = 1e-6). Для этого необходимо, чтобы вы сначала выполнили using OrdinaryDiffEq для доступа к решателям. diffeq по умолчанию имеет следующий вид:

(alg = Tsit5(stagelimiter! = triviallimiter!, steplimiter! = triviallimiter!, thread = static(false)), abstol = 1.0e-6, reltol = 1.0e-6)

Ключевые слова diffeq также могут включать callback дляhttp://docs.juliadiffeq.org/latest/features/callback_functions.html[обработки событий].

Доступны вспомогательные конструкторы CoupledODEs(prob::ODEProblem [, diffeq]) и CoupledODEs(ds::CoupledODEs [, diffeq]).

Примечание разработчика. CoupledODEs является упрощенной оболочкой ODEIntegrator из DifferentialEquations.jl. Интегратор доступен как поле integ, а ODEProblem представляет собой integ.sol.prob. Вспомогательный синтаксис ODEProblem(ds::CoupledODEs, tspan = (t0, Inf)) позволяет найти решение задачи.

# DynamicalSystemsBase.StroboscopicMap — Type

StroboscopicMap <: DiscreteTimeDynamicalSystem
StroboscopicMap(ds::CoupledODEs, period::Real) → smap
StroboscopicMap(period::Real, f, u0, p = nothing; kwargs...)

Динамическая система с дискретным временем, которая создает итерации зависящей от времени (неавтономной системы) CoupledODEs точно за заданный период (period). Вторая сигнатура сначала создает CoupledODEs, а затем вызывает первую.

StroboscopicMap следует интерфейсу DynamicalSystem](tutorial.md#DynamicalSystemsBase.DynamicalSystem). Кроме того, доступна функция set_period!(smap, period), которая задает периоду системы новое значение (как если бы он был параметром). Поскольку эта система работает в дискретном времени, current_time и initial_time являются целыми числами. Начальное время всегда равно 0, потому что current_time считает прошедшие периоды. Вызовите эти функции для родительского элемента (parent) StroboscopicMap, чтобы получить соответствующее значение непрерывного времени. Напротив, [reinit! ожидает t0 в непрерывном времени.

Также доступен

StroboscopicMap(T::Real, f, u0, p = nothing; diffeq, t0 = 0) → smap

вспомогательный конструктор.

См. также описание PoincareMap.

# DynamicalSystemsBase.PoincareMap — Type

PoincareMap <: DiscreteTimeDynamicalSystem
PoincareMap(ds::CoupledODEs, plane; kwargs...) → pmap

Динамическая система с дискретным временем, которая выполняет итерации по отображению Пуанкареlink:Datseris & Parlitz 2022, Nonlinear Dynamics: A Concise Introduction Interlaced with Code, Springer Nature, Undergrad. Lect. Notes In Physics[{caret}DatserisParlitz2022] для заданного непрерывного времени ds. Это отображение определяется как последовательность точек на поверхности сечения Пуанкаре, определенной аргументом plane.

См. также описание StroboscopicMap и poincaresos.

Именованные аргументы

direction = -1: только пересечения с sign(direction) считаются принадлежащими поверхности сечения. Отрицательное направление означает движение от меньшего, чем , к большему, чем .
u0 = nothing: указывает начальное состояние.
rootkw = (xrtol = 1e-6, atol = 1e-8): кортеж NamedTuple именованных аргументов, переданный в find_zero из Roots.jl.
Tmax = 1e3: аргумент Tmax существует для того, чтобы интегратор мог завершить действие вместо бесконечно долгого развития, чтобы избежать случаев, когда итерация будет продолжаться вечно для неопределенных гиперплоскостей или для сходимости к фиксированным точкам, где траектория никогда больше не пересечет гиперплоскость. Если за один step! система эволюционировала более Tmax, то step!(pmap) завершится с выводом ошибки.

Описание

Поверхность сечения Пуанкаре определяется как последовательные трансверсальные пересечения траектории с произвольным многообразием, но в данном случае многообразие должно быть гиперплоскостью. PoincareMap выполняет итерации пересечений сечения.

Если состоянием ds является , то уравнение, определяющее гиперплоскость, имеет вид

где являются параметрами гиперплоскости.

В коде plane может иметь любое значение:

Tuple{Int, <: Real}, как (j, r): плоскость определяется например, когда j-я переменная системы равна значению r.
Вектор длиной D+1. Первые D элементов вектора соответствуют , тогда как последний элемент — .

PoincareMap использует ds, интерполяцию более высокого порядка из DifferentialEquations.jl, и нахождение корней из Roots.jl, чтобы создать высокоточную оценку сечения.

PoincareMap следует интерфейсу DynamicalSystem со следующими аргументами:

dimension(pmap) == dimension(ds), несмотря на то, что отображение Пуанкаре фактически на 1 измерение меньше.
Как и StroboscopicMap, время дискретно и подсчитывает итерации по поверхности сечения. Значение initial_time всегда равно 0, а current_time — это номер текущей итерации.
Новая функция current_crossing_time возвращает реальное время, соответствующее последнему пересечению гиперплоскости, которому также соответствует current_state(ds) .
Для особого случая, когда плоскость (plane) является кортежем Tuple{Int, <:Real}, допускается специальный метод reinit! с входным состоянием длиной D-1 вместо D, т. е. уменьшенное состояние уже на гиперплоскости, которое затем преобразуется в D-мерное состояние.

Пример

using DynamicalSystemsBase
ds = Systems.rikitake(zeros(3); μ = 0.47, α = 1.0)
pmap = poincaremap(ds, (3, 0.0))
step!(pmap)
next_state_on_psos = current_state(pmap)

# DynamicalSystemsBase.ProjectedDynamicalSystem — Type

ProjectedDynamicalSystem <: DynamicalSystem
ProjectedDynamicalSystem(ds::DynamicalSystem, projection, complete_state)

Динамическая система, представляющая собой проекцию существующей системы ds на (проецируемое) пространство.

projection определяет проецируемое пространство. Если projection isa AbstractVector{Int}, то проецируемое пространство — это просто индексы переменных, которые содержит projection. В противном случае проекция (projection) может быть произвольной функцией, которая, учитывая состояние исходной системы ds, возвращает состояние в проецируемом пространстве. В этом случае проецируемое пространство может быть равным исходному или даже иметь более высокую размерность.

complete_state создает состояние для исходной системы из проецируемого состояния. complete_state всегда может быть функцией, которая, учитывая проецируемое состояние, возвращает состояние в исходном пространстве. Однако если projection isa AbstractVector{Int}, то complete_state также может быть вектором, содержащим значения оставшихся переменных системы, т. е. тех, которые не содержатся в проецируемом пространстве. В данном случае проецируемое пространство должно быть более низкоразмерным, чем исходное.

Обратите внимание, что ProjectedDynamicalSystem не требует инвертируемой проекции, complete_state используется только во время reinit!. ProjectedDynamicalSystem на самом деле является довольно тривиальной оболочкой ds, которая считается обычной в исходном пространстве состояний и проецируется только в качестве последнего шага, например во время current_state.

Примеры

Случай 1. Проецирование 5-мерной системы на два последних измерения.

ds = Systems.lorenz96(5)
projection = [4, 5]
complete_state = [0.0, 0.0, 0.0] # завершенное состояние только в плоскости двух последних измерений
pds = ProjectedDynamicalSystem(ds, projection, complete_state)
reinit!(pds, [0.2, 0.4])
step!(pds)
get_state(pds)

Случай 2. Пользовательская проекция на общие функции состояния.

ds = Systems.lorenz96(5)
projection(u) = [sum(u), sqrt(u[1]^2 + u[2]^2)]
complete_state(y) = repeat([y[1]/5], 5)
pds = # то же, что и в примере выше...

# DynamicalSystemsBase.ArbitrarySteppable — Type

ArbitrarySteppable <: DiscreteTimeDynamicalSystem
ArbitrarySteppable(
    model, step!, extract_state, extract_parameters, reset_model!;
    isdeterministic = true, set_state = reinit!,
)

Динамическая система, созданная произвольной «моделью», которая может пошагово выполняться на месте с некоторой функцией step!(model) для 1 шага. Состояние модели извлекается с помощью функции extract_state(model) -> u. Параметры модели извлекаются с помощью функции extract_parameters(model) -> p. Система может быть повторно инициализирована с помощью reinit! с предоставленной пользователем функцией reset_model!, которая должна иметь сигнатуру вызова

reset_model!(model, u, p)

с заданным (потенциально новым) состоянием u и контейнером параметров p, причем для них по умолчанию будут заданы начальные значения в вызове reinit!.

Тип ArbitrarySteppable существует для предоставления интерфейса DynamicalSystems.jl моделям из других пакетов, которые могут использоваться в библиотеке DynamicalSystems.jl. ArbitrarySteppable следует интерфейсу DynamicalSystem со следующими аргументами:

Значение initial_time всегда равно 0, так как время подсчитывает шаги, пройденные моделью с момента создания или последнего вызова reinit!.
Функция set_state! аналогична функции reinit! по умолчанию. В противном случае именованный аргумент set_state является функцией set_state(model, u), которая задает состояние модели равным u.
Необходимо правильно задать ключевое слово isdeterministic, поскольку оно решает, должны ли нижележащие алгоритмы выводить ошибку или нет.

Дополнительные сведения

Для получения дополнительных сведений посетите страницы документации по отдельным пакетам. Более подробную информацию см. на странице Содержимое.