fircls
Расчет коэффициентов многополосного КИХ-фильтра методом наименьших квадратов с ограничениями.
| Библиотека |
|
Синтаксис
Вызов функции
-
b = fircls(n,f,amp,up,lo)— генерирует коэффициентыbКИХ-фильтра с линейной фазовой характеристикой длинойn+1. Амплитудно-частотные характеристики этого фильтра совпадают с характеристиками векторовfиamp. Векторыupиloимеют ту же длину, что иamp. Они определяют верхнюю и нижнюю границы частотной характеристики в каждой полосе.
Аргументы
Входные аргументы
#
n —
порядок фильтра
вещественнозначный положительный скаляр
Details
Порядок фильтра, заданный как вещественный положительный скаляр.
Функция fircls всегда использует четный порядок фильтра для конфигураций с полосой пропускания на частоте Найквиста (т.е. фильтров верхних частот и режекторных фильтров). Это связано с тем, что для нечетных порядков частотная характеристика на частоте Найквиста обязательно равна 0. Если указано нечетное значение n, fircls увеличит его на 1.
|
#
f —
нормализованные частотные точки
вещественнозначный вектор
Details
Нормализованные частотные точки, заданные как вещественнозначный вектор. Частоты перехода находятся в диапазоне [0,1], где 1 соответствует частоте Найквиста. Первая точка f должна быть равна 0, а последняя — 1. Частоты должны быть расположены в порядке возрастания.
#
lo —
нижние границы
вещественнозначный вектор
Details
Нижние границы частотной характеристики в каждой полосе, заданные как вещественнозначный вектор той же длины, что и amp.
Обычно нижнее значение в полосе задерживания указывается отрицательным. При установке lo равным 0 в полосах задерживания получается неотрицательная амплитуда частотной характеристики. Такие фильтры спектрально факторизуются для получения фильтров с минимальной фазой.
|
Входные аргументы «имя-значение»
#
out —
параметры отображения расчета коэффициентов фильтра
:plot | :both
Details
Параметры отображения расчета коэффициентов фильтра, заданные одним из следующих способов:
-
:plot— отображение набора графиков, показывающих амплитудно-частотную характеристику фильтра во всей полосе пропускания и увеличенное изображение амплитудно-частотной характеристики в каждом участке полосы пропускания. Функция обновляет все графики на каждом шаге итерации. Нолики на графике — это предполагаемые экстремумы новой итерации, а крестики — предполагаемые экстремумы предыдущей итерации, где экстремумы — это пики (максимумы и минимумы) пульсаций фильтра. Равными считаются только те пульсации, для которых совпадают нолики и крестики. -
:both— отображение как текстовой информации, так и графиков.
Примеры
Расчет коэффициентов фильтра нижних частот методом наименьших квадратов с ограничениями
Details
Рассчитаем коэффициенты фильтра нижних частот 150-го порядка с нормированной частотой среза рад/отсчет. Укажем максимальную абсолютную погрешность 0.02 в полосе пропускания и 0.01 в полосе задерживания. Отобразим погрешность расчета и амплитудно-частотные характеристики фильтра. Нарушения границ обозначают итерации процедуры по мере сходимости расчета.
import EngeeDSP.Functions: fircls
n = 150
f = [0 0.4 1]
a = [1 0]
up = [1.02 0.01]
lo = [0.98 -0.01]
b = fircls(n, f, a, up, lo; out = :both)Bound Violation = 0.0788344298965972
Bound Violation = 0.009613774499764091
Bound Violation = 0.0005681345753413645
Bound Violation = 5.151994189609224e-6
Bound Violation = 3.486559452259286e-8
Bound Violation = 6.230728155642851e-10
1×151 Matrix{Float64}:
-0.00119101 -0.0040614 … -0.00119101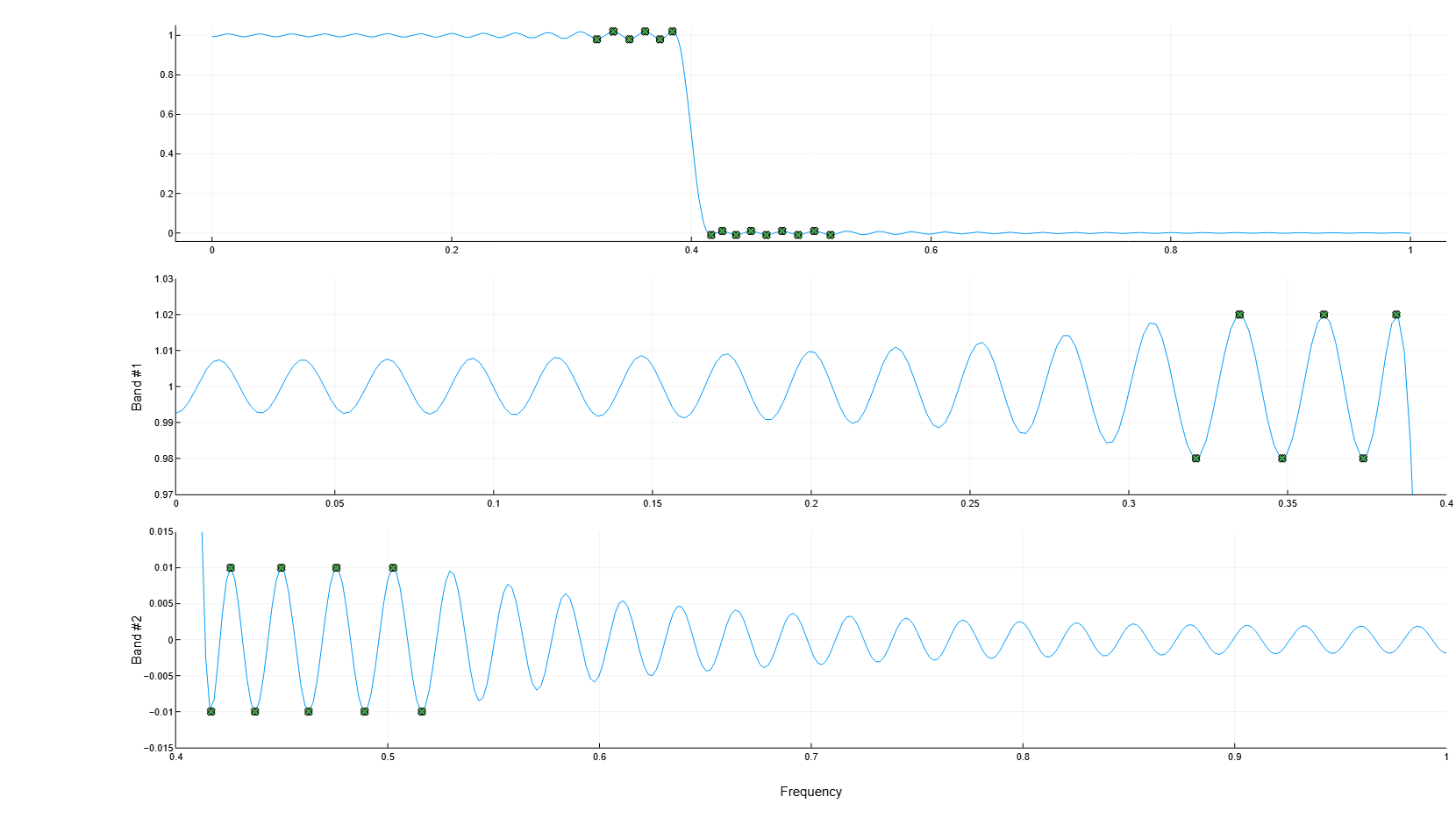
Алгоритмы
Функция fircls использует итерационный алгоритм наименьших квадратов для получения равномерной пульсирующей АЧХ. Алгоритм представляет собой алгоритм многократного обмена, использующий множители Лагранжа и условия Куна—Таккера на каждой итерации.
Литература
-
Selesnick, I. W., M. Lang, and C. S. Burrus. «Constrained Least Square Design of FIR Filters without Specified Transition Bands.» Proceedings of the 1995 International Conference on Acoustics, Speech, and Signal Processing. Vol. 2, 1995, pp. 1260–1263.
-
Selesnick, I. W., M. Lang, and C. S. Burrus. «Constrained Least Square Design of FIR Filters without Specified Transition Bands.» IEEE® Transactions on Signal Processing. Vol. 44, Number 8, 1996, pp. 1879–1892.