alignsignals

Выравнивает два сигнала, задержав самый ранний сигнал.

Библиотека

EngeeDSP

Синтаксис

Вызов функции

xa, ya, D = alignsignals(x, y) — оценивает задержку D между двумя входными сигналами x и y и возвращает D вместе с выровненными сигналами xa и ya. Функция оценивает задержку, используя взаимную корреляцию.
- Если y задержан относительно x, то D положительно, а x задержан на D отсчетов.
- Если y опережает x, то D отрицательно, а y задержан на −D отсчетов.
Входные сигналы не обязательно должны быть точными запаздывающими копиями друг друга. Однако сигналы могут быть точно выровнены только при наличии достаточной корреляции между ними. Подробнее об оценке ковариации и корреляции см. в [1].

xa, ya, D = alignsignals(x, y, Name=Value) — также использует аргументы Name=Value, которые включают метод оценки и опцию усечения входных сигналов. Например, чтобы оценить задержку на основе местоположения наибольшего пика в каждом сигнале, задайте для аргумента Method значение "maxpeak".

Аргументы

Входные аргументы

# x — первый входной сигнал
вектор

Details

Первый входной сигнал, заданный как числовой вектор длины .

Типы данных	`Float32`, `Float64`, `Int8`, `Int16`, `Int32`, `Int64`, `UInt8`, `UInt16`, `UInt32`, `UInt64`
Поддержка комплексных чисел	Да

# y — второй входной сигнал
вектор

Details

Второй входной сигнал, заданный как числовой вектор длины .

Типы данных	`Float32`, `Float64`, `Int8`, `Int16`, `Int32`, `Int64`, `UInt8`, `UInt16`, `UInt32`, `UInt64`
Поддержка комплексных чисел	Да

Входные аргументы «имя-значение»

Укажите необязательные пары аргументов в формате Name=Value, где Name — имя аргумента, а Value — соответствующее значение. Аргументы типа Name=Value должны располагаться после других аргументов, но порядок пар не имеет значения.

# Method — метод оценки задержки между сигналами
"xcorr" (по умолчанию) | "maxpeak" | "npeak" | "risetime"

Details

Метод оценки задержки между сигналами, указанными как "xcorr", "maxpeak", "npeak" или "risetime". Вы можете указать дополнительные аргументы «имя-значение» в зависимости от указанного Method:

"xcorr" — оценка задержки с использованием взаимной корреляции. Если метод указан как "xcorr", то можно также указать MaxLag;
"maxpeak" — оценка задержки с использованием положения самого высокого пика в каждом сигнале. Если метод указан как "maxpeak", то можно дополнительно указать MinPeakProminence и MinPeakHeight;
"npeak" — оценка задержки с использованием положения -го пика в каждом сигнале. Если метод указан как "npeak", то можно дополнительно указать PeakNum, MinPeakProminence и MinPeakHeight;
"risetime" — оценка задержки с использованием положения нарастающих фронтов в каждом сигнале. Функция использует указанные значения StateLevels для поиска нарастающих фронтов.

# MaxLag — максимальный размер окна
скаляр

Details

Максимальный размер окна, используемый для оценки задержки между сигналами, задается как целочисленный скаляр. По умолчанию MaxLag равен , где — длина x, а — длина y. Если MaxLag отрицателен, то функция использует абсолютное значение.

Этот аргумент используется только в том случае, если для аргумента Method задано значение "xcorr".

Типы данных

Float32, Float64, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64

# PeakNum — номер пика
скаляр

Details

Номер пика, используемый для выравнивания сигналов, задается как положительный целочисленный скаляр. Этот аргумент используется только в том случае, если для аргумента Method задано значение "npeak".

Типы данных

Float32, Float64, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64

# MinPeakProminence — минимальное возвышение пика
скаляр

Details

Минимальное возвышение пика, используемое для идентификации пиков в сигналах, задается как вещественный неотрицательный скаляр. При указании MinPeakProminence функция находит пики, относительная значимость которых не менее указанного значения. Подробнее см. в разделе Возвышения.

Этот аргумент используется только в том случае, если для аргумента Method задано значение "npeak" или "maxpeak".

Типы данных

Float32, Float64, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64

# MinPeakHeight — минимальная высота пика
скаляр

Details

Минимальная высота пика, используемая для определения пиков в сигналах, задается как вещественный скаляр. При указании MinPeakHeight функция находит пики, высота которых превышает указанное значение. Подробнее см. в findpeaks.

Этот аргумент используется только в том случае, если для аргумента Method задано значение "npeak" или "maxpeak".

Типы данных

Float32, Float64, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64

# StateLevels — уровни состояний
двухэлементный вектор-строка

Details

Уровни состояний, заданные как вещественный двухэлементный вектор-строка. Первый элемент соответствует низкому уровню состояния входных сигналов, а второй — высокому уровню состояния входных сигналов. Если значение StateLevels не указано, то функция оценивает уровни состояний входного сигнала методом гистограммы.

Подробнее см. в risetime.

Этот аргумент используется только в том случае, если для аргумента Method задано значение "risetime".

Типы данных

Float64

# Truncate — опция усечения входных сигналов
false (0) (по умолчанию) | true (1)

Details

Опция усечения входных сигналов, заданная числовой или логической true (1) или false (0). При указании значения true (1) для аргумента Truncate длины xa и ya равны длинам x и y соответственно.

Если расчетная задержка D положительна, то функция добавляет D нулей к x и усекает последние D отсчетов x.
Если D отрицательна, то функция добавляет −D нулей к y и усекает последние D отсчетов y.
Если D , то xa состоит из нулей, и все отсчеты x теряются. Если −D , то ya состоит из нулей, и все отсчеты y теряются.

Выходные аргументы

# xa — выровненный первый сигнал
вектор

Details

Выровненный первый сигнал, возвращенный в виде числового вектора, выровненного со вторым выходным аргументом ya.

Если входной аргумент x — вектор-строка, то xa также является вектором-строкой.
Если входной аргумент x — вектор-столбец, то xa также является вектором-столбцом.

Если для аргумента Truncate задано значение true, а расчетная задержка D положительна, то xa эквивалентен входному сигналу x с D добавленными нулями и усеченными последними D отсчетами.

# ya — выровненный второй сигнал
вектор

Details

Выровненный второй сигнал, возвращенный в виде числового вектора, выровненного со вторым выходным аргументом xa.

Если входной аргумент y — вектор-строка, то ya также является вектором-строкой.
Если входной аргумент y — вектор-столбец, то ya также является вектором-столбцом.

Если для аргумента Truncate задано значение true, а расчетная задержка D отрицательна, то ya эквивалентен входному сигналу y с −D добавленными нулями и усеченными последними −D отсчетами.

# D — расчетная задержка между входными сигналами
целочисленный скаляр

Details

Расчетная задержка между входными сигналами, возвращаемая в виде целочисленного скаляра. Это значение представляет собой количество отсчетов, на которое смещены два входных сигнала x и y.

Если y отстает относительно x, то D положительно, а x отстает на D отсчетов.
Если y опережает x, то D отрицательно, а y отстает на −D отсчетов.
Если x и y уже выровнены, то D равно нулю, и ни x, ни y не задерживаются.

Если указано значение входного аргумента MaxLag, то D будет меньше или равно MaxLag.

Примеры

Выравнивание двух сигналов, если первый сигнал отстает на три отсчета

Details

Создадим два сигнала: x и y. Сигнал x — это то же самое, что y, за исключением того, что у x в начале три нуля и один дополнительный в конце. Выровняем два сигнала.

import EngeeDSP.Functions: alignsignals

x = [0, 0, 0, 1, 2, 3, 0, 0]
y = [1, 2, 3, 0]

xa, ya, D = alignsignals(x, y)

(xa = [0, 0, 0, 1, 2, 3, 0, 0], ya = [0, 0, 0, 1, 2, 3, 0], D = -3)

Выравнивание двух сигналов, если второй сигнал отстает на два отсчета

Details

Создадим два сигнала: x и y. Сигнал y — это то же самое, что x, за исключением того, что y задерживается на два отсчета. Выровняем два сигнала.

import EngeeDSP.Functions: alignsignals

x = [1, 2, 3]
y = [0, 0, 1, 2, 3]

xa, ya, D = alignsignals(x, y)

(xa = [0, 0, 1, 2, 3], ya = [0, 0, 1, 2, 3], D = 2)

Выровняем сигналы, используя максимальный размер окна 1:

maxlag = 1
xa, ya, D = alignsignals(x, y, Method="xcorr", MaxLag=maxlag)

(xa = [0, 1, 2, 3], ya = [0, 0, 1, 2, 3], D = 1)

Выравнивание двух двухуровневых сигналов по нарастающим фронтам

Details

Сгенерируем два сигнала, представляющих собой двухуровневые сигналы. Сигналы имеют частоту дискретизации 50 Гц в течение 20 секунд. Для первого сигнала переход происходит через 13 секунд после начала измерения. Для второго сигнала переход происходит через 5 секунд после начала измерения. Сигналы имеют разные амплитуды и находятся в белом гауссовском шуме с различными дисперсиями. Построим графики сигналов.

t = range(0, 20, length=1001)

e1 = 1.4 .* tanh.(t .- 13) .+ randn(length(t)) ./ 3
e2 = tanh.(3 .* (t .- 5)) .+ randn(length(t)) ./ 5

plot(t, e1, label="e1")
plot!(t, e2, label="e2")
xlabel!("Seconds")
ylabel!("Amplitude")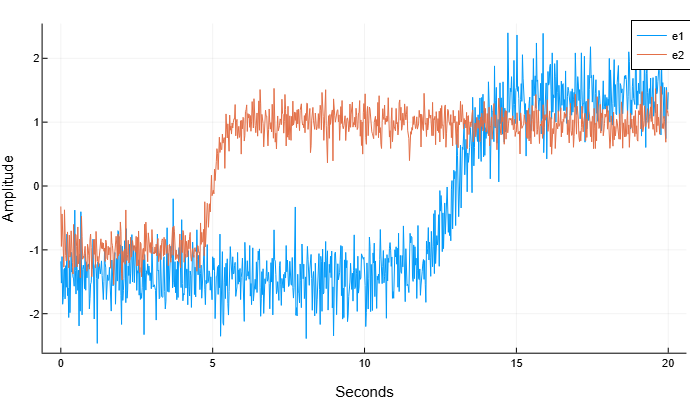

alignsignals 1

Выровняем сигналы так, чтобы их времена перехода совпадали.

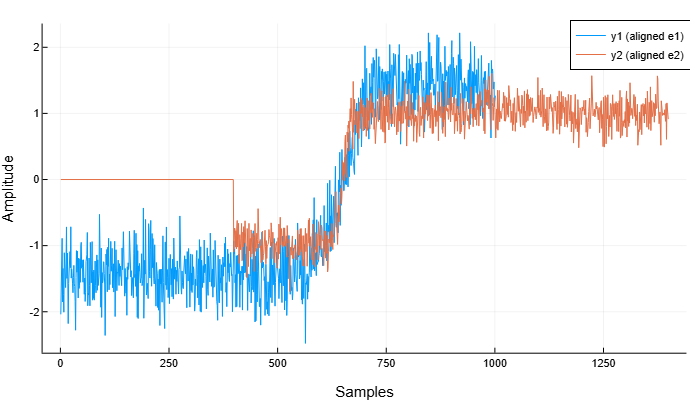
Корреляционные методы не позволяют адекватно выровнять этот тип сигналов:

y1, y2 = alignsignals(e1, e2)

plot(y1, label="y1 (aligned e1)")
plot!(y2, label="y2 (aligned e2)")
xlabel!("Samples")
ylabel!("Amplitude")

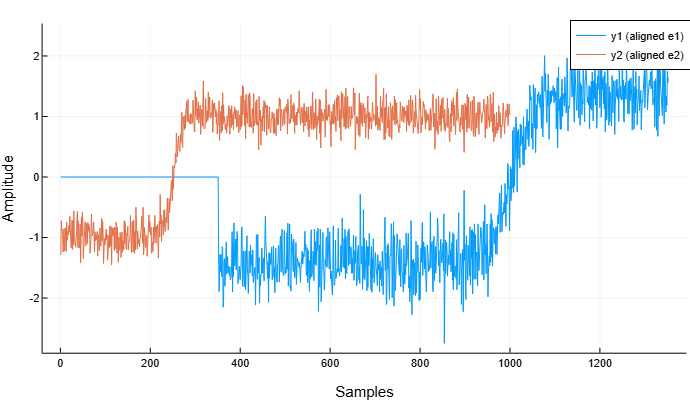
alignsignals 2

Выровняем сигналы, используя метод "risetime":

y1, y2 = alignsignals(e1, e2, Method="risetime")

plot(y1, label="y1 (aligned e1)")
plot!(y2, label="y2 (aligned e2)")
xlabel!("Samples")
ylabel!("Amplitude")

alignsignals 3

Литература

Orfanidis, Sophocles J. Optimum Signal Processing. An Introduction. 2nd Ed. Englewood Cliffs, NJ: Prentice-Hall, 1996.