spectralSkewness

Спектральная асимметрия сигналов и спектрограмм.

Библиотека

EngeeDSP

Синтаксис

Вызов функции

skewness,spread,centroid = spectralSkewness(x,f) — возвращает спектральную асимметрию сигнала x с течением времени. Также возвращает спектральную протяженность и спектральный центроид. Интерпретация x функцией зависит от формы f.

skewness,spread,centroid = spectralSkewness(x,f,Name,Value) — задает параметры с использованием одного или нескольких аргументов типа «имя-значение».

spectralSkewness(___;out=:plot) — строит график спектральной асимметрии.
- Если входной сигнал находится во временной области, график спектральной асимметрии строится в зависимости от времени.
- Если входной сигнал находится в частотной области, график спектральной асимметрии строится в зависимости от номера кадра.

Аргументы

Входные аргументы

# x — входной сигнал
вектор-столбец | матрица

Details

Входной сигнал, заданный как вектор или матрица. Интерпретация x функцией зависит от формы f.

Типы данных

Float32, Float64

# f — частота дискретизации или вектор частот (Гц)
скаляр | вектор

Details

Частота дискретизации или вектор частот в Гц, заданные как скаляр или вектор соответственно. Интерпретация x функцией зависит от формы f:

Если f — скаляр, x интерпретируется как сигнал во временной области, а f — как частота дискретизации. В этом случае x должен быть вещественным вектором или матрицей. Если x задан как матрица, столбцы интерпретируются как отдельные каналы.
Если f — вектор, x интерпретируется как сигнал в частотной области, а f — как частоты в Гц, соответствующие строкам x. В этом случае x должен быть вещественным массивом размером , где — количество спектральных значений на заданных частотах f, — количество отдельных спектров, а — количество каналов.
Количество строк x, , должно быть равно количеству элементов f.

Типы данных

Float32, Float64

Входные аргументы «имя-значение»

Укажите необязательные пары аргументов в виде Name,Value, где Name — имя аргумента, а Value — соответствующее значение. Аргументы типа «имя-значение» должны располагаться после других аргументов, но порядок пар не имеет значения.

Используйте запятые для разделения имени и значения, а Name заключите в кавычки.

Следующие аргументы типа «имя-значение» применяются, если x — сигнал во временной области. Если x — сигнал в частотной области, аргументы типа «имя-значение» игнорируются.

# Window — окно, применяемое во временной области
rectwin(round(f*0.03)) (по умолчанию) | вектор

Details

Окно, применяемое во временной области, заданное как вещественный вектор. Количество элементов вектора должно находиться в диапазоне [1,size(x,1)]. Количество элементов вектора также должно быть больше OverlapLength.

Типы данных

Float32, Float64

# OverlapLength — количество отсчетов, перекрывающихся между соседними окнами
round(f*0.02) (по умолчанию) | неотрицательный скаляр

Details

Количество отсчетов, перекрывающихся между соседними окнами, заданное как целое число в диапазоне [0,size(Window,1)).

Типы данных

Float32, Float64

# FFTLength — количество элементов в ДПФ
numel(Window) (по умолчанию) | положительный целочисленный скаляр

Details

Количество элементов, используемых для вычисления ДПФ оконных входных выборок, заданное как положительный целочисленный скаляр. Если не аргумент не задан, FFTLength по умолчанию равен количеству элементов в Window.

Типы данных

Float32, Float64

# Range — диапазон частот (Гц)
[0,f/2] (по умолчанию) | двухэлементный вектор-строка

Details

Диапазон частот в Гц, заданный как двухэлементный вектор-строка возрастающих вещественных значений в диапазоне [0,f/2].

Типы данных

Float32, Float64

# SpectrumType — тип спектра
"power" (по умолчанию) | "magnitude"

Details

Тип спектра, заданный как "power" или "magnitude":

"power" — спектральная асимметрия рассчитывается для одностороннего спектра мощности;
"magnitude" — спектральная асимметрия рассчитывается для одностороннего амплитудного спектра.

Типы данных

String

# out — тип выходных данных
:data (по умолчанию) | :plot

Details

Тип выходных данных:

:data — функция возвращает данные;
:plot — функция возвращает график.

Выходные аргументы

# skewness — спектральная асимметрия
скаляр | вектор | матрица

Details

Спектральная асимметрия, возвращаемая в виде скаляра, вектора или матрицы. Каждая строка skewness соответствует спектральной асимметрии окна x. Каждый столбец skewness соответствует независимому каналу.

# spread — спектральная протяженность
скаляр | вектор | матрица

Details

Спектральная протяженность, возвращаемая в виде скаляра, вектора или матрицы. Каждая строка spread соответствует спектральной протяженности окна x. Каждый столбец spread соответствует независимому каналу.

# centroid — спектральный центроид
скаляр | вектор | матрица

Details

Спектральный центроид, возвращаемый в виде скаляра, вектора или матрицы. Каждая строка centroid соответствует спектральному центроиду окна x. Каждый столбец centroid соответствует независимому каналу.

Примеры

Спектральная асимметрия сигнала во временной области

Details

Создадим ЛЧМ-сигнал с белым гауссовским шумом и рассчитаем асимметрию, используя параметры по умолчанию.

import EngeeDSP.Functions: chirp, randn, spectralSkewness

fs = 1000
t = (0:1/fs:10)
f1 = 300
f2 = 400
x = chirp(t, f1, 10, f2) + randn(length(t), 1)

skewness = spectralSkewness(x, fs)

Построим график зависимости спектральной асимметрии от времени.

spectralSkewness(x, fs, out=:plot)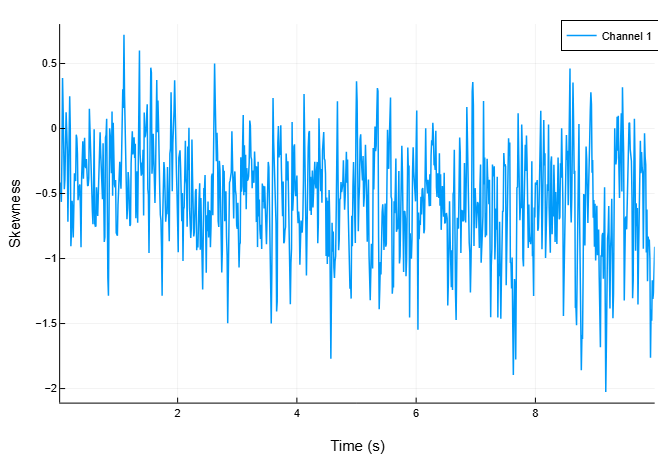

spectralSkewness 1

([-0.41584882984851185, -0.5170941305241857, -0.564347048766862, -0.20108069594499398, 0.3892427522273517, 0.1463327742296114, -0.0959324772116146, -0.4664806868967973, -0.3923963888464158, 0.01796837401846083  …  -0.853109771702925, -1.0019652539560882, -1.7630883535558604, -1.3928510876449312, -1.4782180105459737, -1.1673132825372987, -1.3108237989573261, -1.2622253537332102, -1.1392100073297082, -0.9096598411870619], [137.66250718402654, 127.45803470472126, 128.62674026296034, 129.186501587399, 127.21238231874466, 135.27228568052246, 114.29332508288279, 113.20360160889103, 129.60154758930983, 137.04900834348766  …  113.02519942099786, 138.35361563650906, 110.54777802801922, 115.82292236038828, 113.2157408305658, 124.01480122917285, 126.18012726969127, 136.32543128218506, 152.2965330188322, 151.53661288017915], [232.54635888820377, 244.52603810295574, 263.6019775735153, 271.04043285763873, 267.14685957025756, 275.70362962545187, 270.28792339138397, 255.93688502474646, 268.74572871366905, 274.7291310293522  …  320.08685981196544, 317.87764929627133, 349.6998379422504, 332.2649969853749, 344.80178074508837, 339.5576123782947, 326.9848093500554, 318.2941806082642, 311.10184808692037, 296.1414058613318], Plot{Plots.PlotlyJSBackend() n=1})

Спектральная асимметрия сигнала в частотной области

Details

Создадим ЛЧМ-сигнал с белым гауссовским шумом, а затем рассчитаем спектрограмму с помощью функции stft.

import EngeeDSP.Functions: chirp, randn, stft

fs = 1000
t = (0:1/fs:10)'
f1 = 300
f2 = 400
x = chirp(t, f1, 10, f2) + randn(size(t)...)

s, f = stft(x, fs, "FrequencyRange", "onesided")
s = abs.(s).^2

Рассчитаем асимметрию спектрограммы с течением времени.

import EngeeDSP.Functions: spectralSkewness

skewness = spectralSkewness(s, f)

Построим график зависимости спектральной асимметрии от номера кадра.

spectralSkewness(s, f, out=:plot)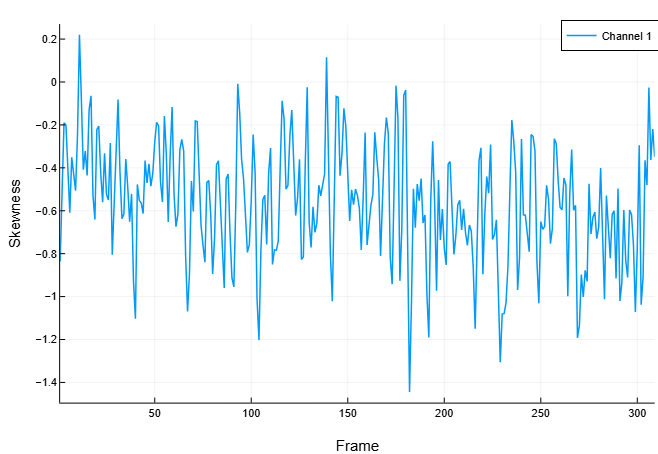

spectralSkewness 2

([-0.8359982931981216, -0.5281233777476992, -0.19003913028541924, -0.20010790649073676, -0.4518215729934591, -0.609505728606324, -0.35104046557619795, -0.44243240701247855, -0.5058598909702079, -0.24334848229314177  …  -0.7652817638675459, -0.29454858120347277, -1.0382786281369654, -0.9085777404108826, -0.3647202399233729, -0.4806516533252003, -0.025478934806172537, -0.3634101240910118, -0.2187538302761354, -0.34903020983974686], [107.17221169316268, 108.08710344363071, 121.73703765712227, 127.2733133823049, 113.45452035995662, 101.935212957374, 118.00182469240174, 132.80689180278688, 115.59164488540159, 103.25800480469758  …  130.74712793061693, 140.8136649111479, 120.8114483851076, 126.27406132641096, 143.9703528142779, 132.1095322961261, 137.9399485601707, 131.12441824862063, 144.70449053384257, 164.38033907467928], [292.7910624802788, 275.40970236507655, 244.1866329141813, 254.4473178753846, 253.6161996745867, 275.82905121269937, 272.98722964342187, 226.80470629232215, 236.10533279943394, 239.64514680772058  …  321.87682998876653, 278.83384299634093, 314.86016584163775, 305.56640901528647, 280.8820142043897, 288.72754980225983, 261.32008807500637, 273.0967688666202, 243.65572527972142, 256.13120365040834], Plot{Plots.PlotlyJSBackend() n=1})

Указание параметров, отличных от стандартных

Details

Создадим ЛЧМ-сигнал с белым гауссовским шумом.

import EngeeDSP.Functions: chirp, randn

fs = 1000
t = (0:1/fs:10)
f1 = 300
f2 = 400
x = chirp(t, f1, 10, f2) + randn(length(t), 1)

Рассчитаем асимметрию спектра мощности с течением времени. Рассчитаем асимметрию для окон Хэмминга длительностью 50 мс с перекрытием 25 мс. Используем диапазон от 62.5 Гц до fs/2 для расчета асимметрии.

import EngeeDSP.Functions: spectralSkewness, hamming

skewness = spectralSkewness(x, fs,
                      "Window", hamming(round(Int, 0.05*fs)),
                      "OverlapLength", round(Int, 0.025*fs),
                      "Range", [62.5, fs/2])

Построим график зависимости асимметрии от времени.

spectralSkewness(x, fs,
              "Window", hamming(round(Int, 0.05*fs)),
              "OverlapLength", round(Int, 0.025*fs),
              "Range", [62.5, fs/2],
              out=:plot)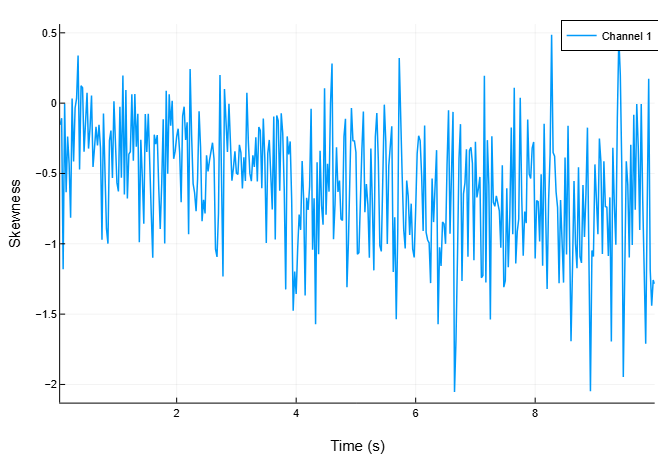

spectralSkewness 3

([-0.15358670202573538, -0.10674901633061454, -1.1800361499235466, -0.004310190890005931, -0.6333699707463635, -0.23684625667693265, -0.43005228049825217, -0.8150523711899812, 0.03350102205262587, -0.41422126904743767  …  -0.005625970564356666, -0.6911434383476336, -1.3456964659853543, -1.710416093386148, -0.7442772354709529, 0.17283689627442853, -1.180419434083617, -1.440520104825559, -1.2583907091166355, -1.2842556849576383], [110.53667066154323, 81.12551758487213, 76.00441845155343, 97.84638979421082, 73.30917024731693, 106.73269627867673, 86.62588932286765, 96.51841858083655, 103.85455951559621, 81.25600340707545  …  130.74893548874454, 125.17411282084814, 105.79471192625837, 82.20506434500429, 112.9987914008663, 118.82027872700775, 91.5641846600464, 86.79996258356996, 97.9073613532983, 97.76881671452485], [288.3573645373158, 301.453120754697, 281.81310005697344, 266.79710402702926, 294.40582264869937, 251.81256307415043, 296.03366939785593, 326.86271852855765, 268.5491461338446, 302.8114318001578  …  265.2072744080883, 317.3863334548424, 333.8375132973837, 354.45727064830913, 338.77406994099954, 266.7769262524174, 342.5369659108678, 348.9119484862638, 341.65454501607263, 342.4239901408415], Plot{Plots.PlotlyJSBackend() n=1})

Алгоритмы

Спектральная асимметрия рассчитывается, как описано в [1]:

где

— частота в Гц, соответствующая бину ;
— спектральное значение в бине ;
и — границы полосы в бинах, по которым рассчитывается спектральная асимметрия;
— спектральный центроид;
— спектральная протяженность.

Литература

Peeters, G. «A Large Set of Audio Features for Sound Description (Similarity and Classification) in the CUIDADO Project.» Technical Report; IRCAM: Paris, France, 2004.