instfreq

Оценка мгновенной частоты.

Библиотека

EngeeDSP

Синтаксис

Вызов функции

ifq = instfreq(x,fs) — оценивает мгновенную частоту сигнала x, дискретизированного с частотой fs. Если x — матрица, то функция оценивает мгновенную частоту независимо для каждого столбца и возвращает результат в соответствующем столбце ifq.

ifq = instfreq(x,t) — оценивает мгновенную частоту x, измеренную в моменты времени, хранящиеся в t.

ifq = instfreq(tfd,fd,td) — оценивает мгновенную частоту сигнала, частотно-временное распределение tfd которого дискретизируется при значениях частоты, хранящихся в fd, и значениях времени, хранящихся в td.

ifq = instfreq(___,Name=Value) — задает дополнительные параметры для любого из предыдущих синтаксисов, используя аргументы типа «имя-значение». Вы можете указать алгоритм, используемый для оценки мгновенной частоты, или пределы частоты, используемые в вычислении.

ifq,t = instfreq(___) — также возвращает t, вектор периодов дискретизации, соответствующий ifq.

instfreq(___) — без выходных аргументов отображает расчетную мгновенную частоту.

Аргументы

Входные аргументы

# x — входной сигнал
вектор | матрица

Details

Входной сигнал, заданный как вектор или матрица. Если x — вектор, то instfreq обрабатывает его как одиночный канал. Если x — матрица, то функция вычисляет мгновенную частоту независимо для каждого столбца и возвращает результат в соответствующем столбце функции ifq.

Типы данных	`Float32`, `Float64`
Поддержка комплексных чисел	Да

# fs — частота дискретизации
положительный скаляр

Details

Частота дискретизации, заданная как положительный скаляр. Частота дискретизации — это количество отсчетов в единицу времени. Если единицей времени являются секунды, то частота дискретизации указывается в Гц.

Типы данных

Float32, Float64, Int8, Int16, Int32, Int64, UInt8, UInt16, UInt32, UInt64

# t — периоды дискретизации
вещественный вектор

Details

Периоды дискретизации, заданные как вещественный вектор.

Вещественный вектор — момент времени, соответствующий каждому элементу x.

Типы данных

Float32, Float64

# tfd — частотно-временное распределение
матрица

Details

Частотно-временное распределение, заданное как матрица, дискретизированная с частотами, хранящимися в fd, и значениями времени, хранящимися в td. Этот входной аргумент поддерживается только при выборе значения "tfmoment" для аргумента Method.

Типы данных

Float32, Float64

# fd,td — значения частоты и времени для частотно-временного распределения
векторы

Details

Значения частоты и времени для частотно-временного распределения, заданные как векторы. Эти входные аргументы поддерживаются только при выборе значения "tfmoment" для аргумента Method.

Типы данных

Float32, Float64

Входные аргументы «имя-значение»

Укажите необязательные пары аргументов в виде Name=Value, где Name — имя аргумента, а Value — соответствующее значение. Аргументы типа «имя-значение» должны располагаться после других аргументов, но порядок пар не имеет значения.

# FrequencyLimits — диапазон частот
[0 fs/2] (по умолчанию для вещественных сигналов) | [-fs/2 fs/2] (по умолчанию для комплексных сигналов) | двухэлементный вектор

Details

Диапазон частот, заданный как двухэлементный вектор в Гц. Если FrequencyLimits не задан, этот аргумент по умолчанию равен [0 fs/2] для вещественных сигналов и [-fs/2 fs/2] для комплексных сигналов. Этот аргумент поддерживается только при выборе значения "tfmoment" для аргумента Method.

Типы данных

Float32, Float64

# Method — метод вычисления
"tfmoment" (по умолчанию) | "hilbert"

Details

Метод вычисления, указанный как "tfmoment" или "hilbert".

"tfmoment" — вычисляет мгновенную частоту как первый условный спектральный момент частотно-временного распределения x. Если x имеет неравномерную дискретизацию, функция интерполирует сигнал на равномерную сетку для вычисления мгновенных частот.
"hilbert" — вычисляет мгновенную частоту как производную фазы аналитического сигнала x, найденного с помощью преобразования Гильберта. Этот метод принимает только равномерно дискретизированные действительные сигналы и не поддерживает входные данные частотно-временного распределения.

# out — тип выходных данных
:data (по умолчанию) | :plot

Details

Тип выходных данных:

:data — функция возвращает данные;
:plot — функция возвращает график.

Выходные аргументы

# ifq — мгновенная частота
вектор | матрица

Details

Мгновенная частота, возвращаемая в виде вектора или матрицы с теми же размерами, что и входные данные.

Типы данных

Float32, Float64

# t — оценки времени частоты
вещественный вектор

Details

Оценки времени частоты, возвращаемые в виде вещественного вектора.

Типы данных

Float32, Float64

Если t, fd или td имеют одинарную точность, а входной вектор или матрица — двойную точность, то функция возвращает результат с одинарной точностью. Тип выходных данных не зависит от типа данных частоты дискретизации.

Примеры

Мгновенная частота нестационарного сигнала

Details

Сгенерируем сигнал с частотой дискретизации 5 кГц длительностью 4 секунды. Сигнал состоит из набора импульсов уменьшающейся длительности, разделенных областями колебаний амплитуды и изменяющейся частоты с тенденцией к увеличению. Построим график сигнала.

Pkg.add(["SpecialFunctions", "SignalAnalysis"])
using SpecialFunctions, SignalAnalysis
import EngeeDSP.Functions: instfreq

fs = 5000
t = 0:1/fs:4-1/fs

s = besselj.(0, 1000 .* (sin.(2*pi*t.^2/8).^4))

plot(t, s)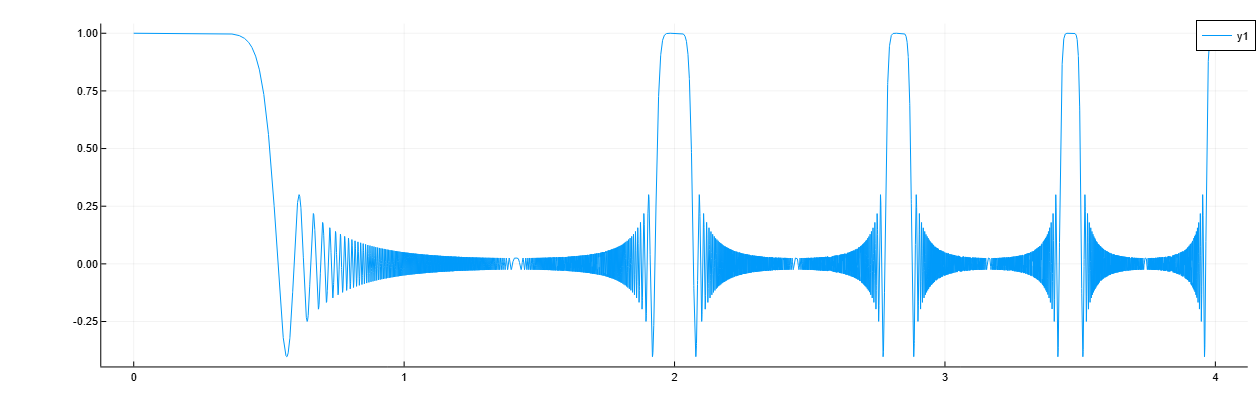

instfreq 1

Оценим зависящую от времени частоту сигнала в качестве первого момента спектрограммы мощности. Построим спектрограмму мощности и наложим на нее мгновенную частоту.

instfreq(s, fs, out=:plot)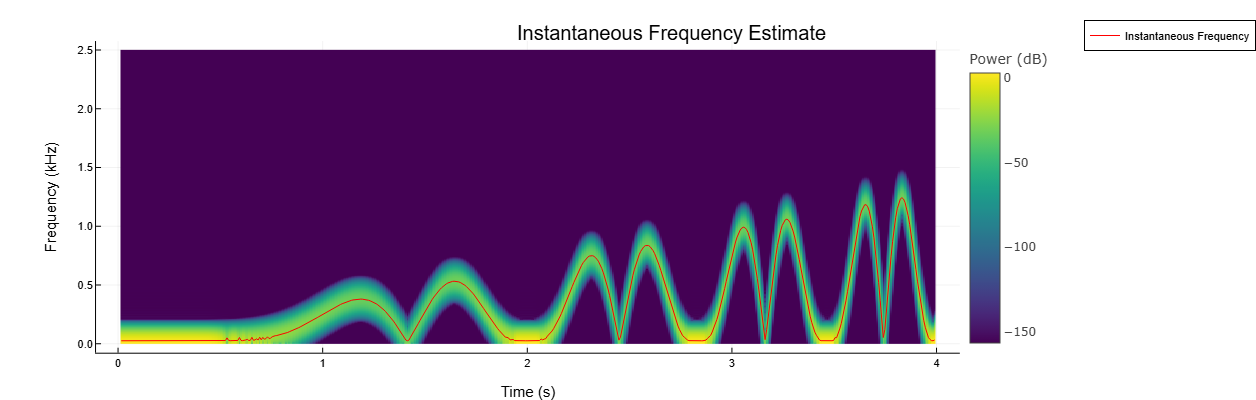

instfreq 2

Мгновенная частота комплекснозначного сигнала

Details

Сгенерируем комплекснозначный сигнал, состоящий из чирпа с синусоидально изменяющейся частотой. Сигнал дискретизируется на частоте 3 кГц в течение 1 секунды, и к нему прибавляется белый гауссовский шум.

import EngeeDSP.Functions: instfreq

fs = 3000
t = 0:1/fs:1-1/fs
x = exp.(2im*pi*100*cos.(2*pi*2*t)) + randn(size(t))/100

Оценим зависящую от времени частоту сигнала как первый момент спектрограммы мощности. Это единственный метод, который функция instfreq поддерживает для комплекснозначных сигналов. Построим спектрограмму мощности и наложим на нее мгновенную частоту.

instfreq(x, t, out=:plot)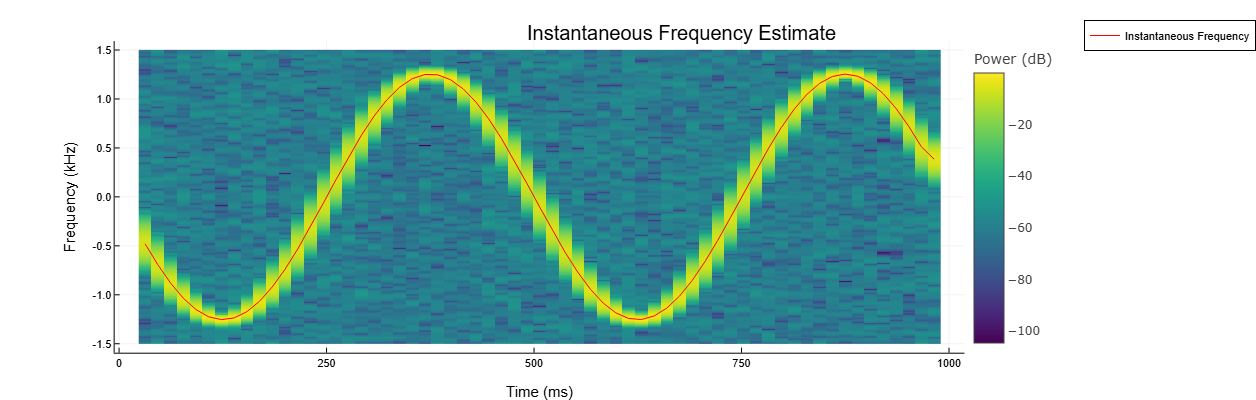

instfreq 3

Мгновенная частота многоканального сигнала

Details

Создадим двухканальный сигнал, дискретизируемый с частотой 1 кГц в течение 2 секунд, состоящий из двух каналов.

В первом канале мгновенная частота изменяется со временем в виде пилообразной волны, максимум которой приходится на 75% периода.
Во втором канале мгновенная частота изменяется со временем в виде прямоугольной волны с коэффициентом заполнения 30.

import EngeeDSP.Functions: instfreq, sawtooth, square

fs = 1000
t = 0:1/fs:2
x = [sawtooth.(2*pi*t, 0.75) square.(2*pi*t, 30)]

plot(t, x)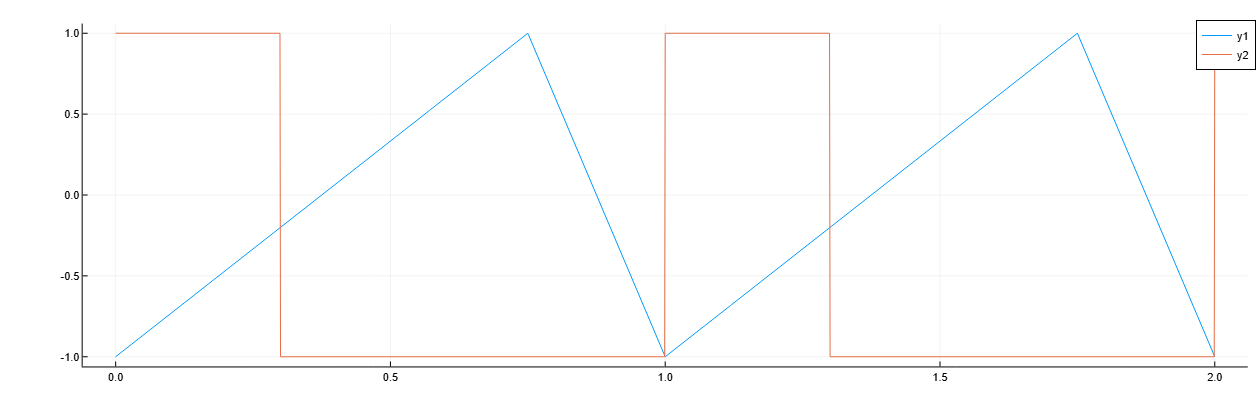

instfreq 4

Вычислим и отобразим мгновенную частоту.

instfreq(x, t, out=:plot)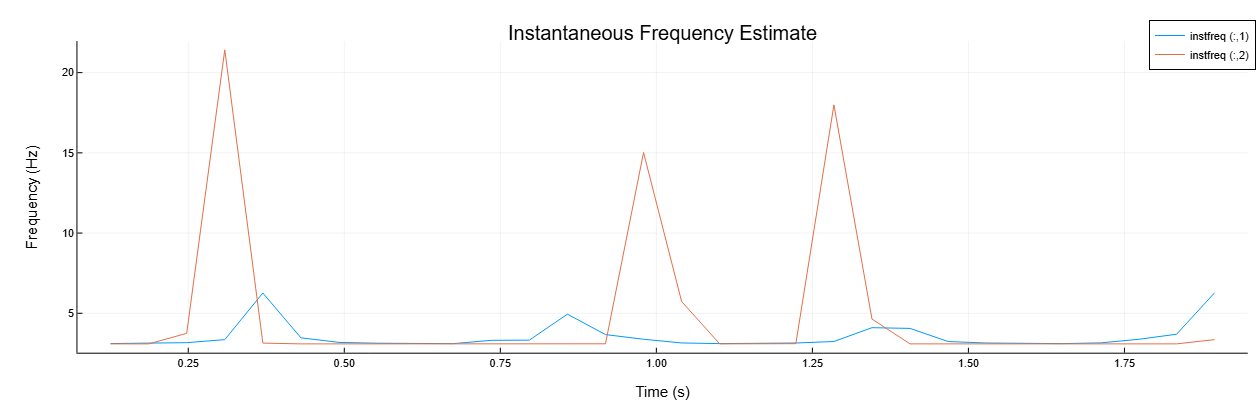

instfreq 5

Мгновенная частота чирп-сигнала

Details

Сгенерируем чирп-сигнал, модулированный гауссовой функцией. Зададим частоту дискретизации 2 кГц и длительность сигнала 4 с.

import EngeeDSP.Functions: instfreq, pspectrum

fs = 2000
t = 0:1/fs:4-1/fs

q = real(chirp(0, 500, 4, fs)) .* exp.(-1.7*(t.-2).^2)

plot(t, q)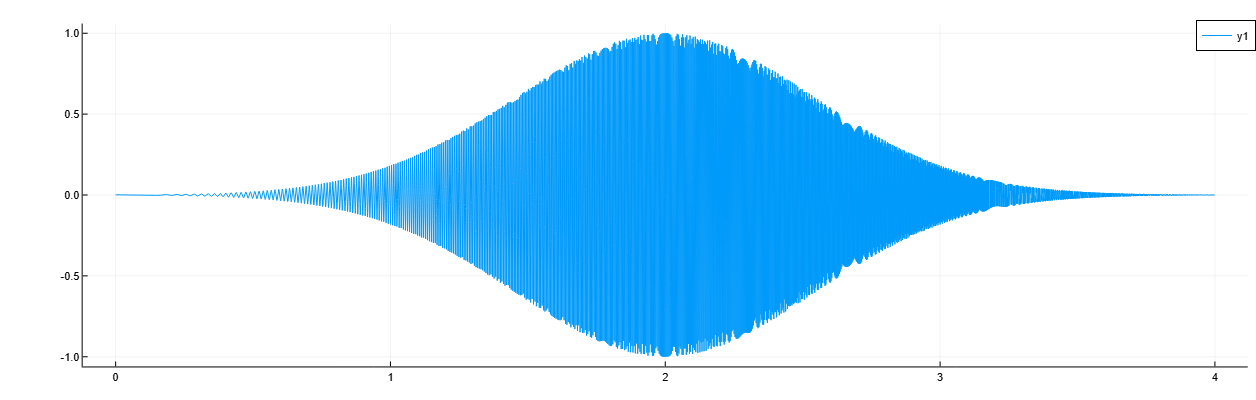

instfreq 6

Используем функцию pspectrum с настройками по умолчанию для оценки спектра мощности сигнала. Используем оценку для вычисления мгновенной частоты.

p, f, t = pspectrum(q, fs, "spectrogram")

instfreq(p, f, t, out=:plot)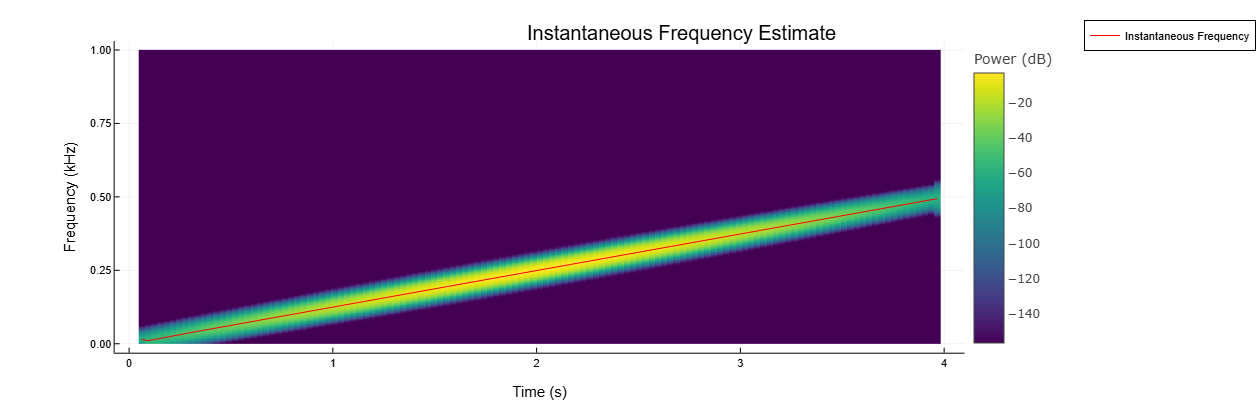

instfreq 7

Мгновенная частота синусоиды

Details

Сгенерируем синусоидальный сигнал, дискретизированный с частотой 1 кГц в течение 0.3 секунд и дополненный белым гауссовым шумом с дисперсией 1/16. Зададим частоту синусоиды 200 Гц. Оценим и отобразим мгновенную частоту сигнала.

import EngeeDSP.Functions: instfreq, pspectrum

fs = 1000
t = 0:1/fs:0.3-1/fs

x = sin.(2*pi*200*t) .+ randn(size(t))/4

instfreq(x, t, out=:plot)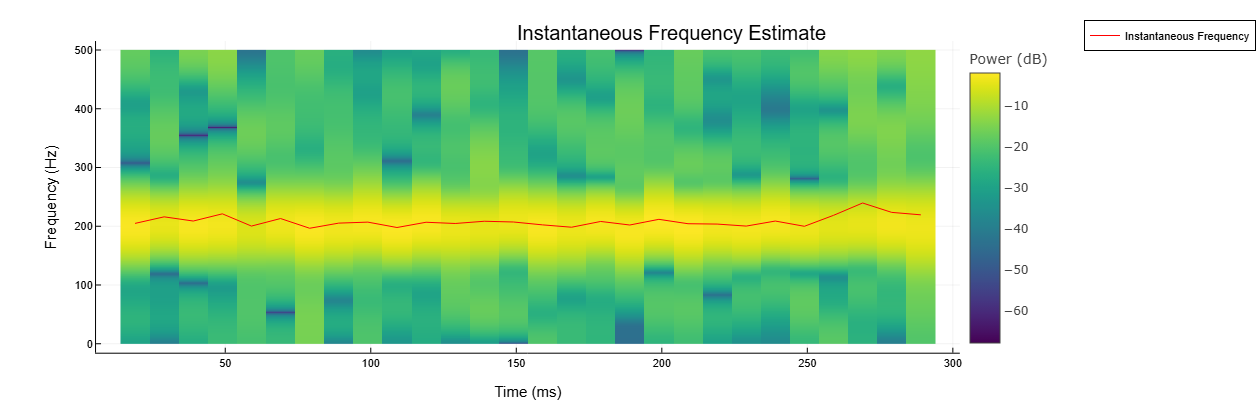

instfreq 8

Снова оценим мгновенную частоту сигнала, но теперь в качестве входных данных используем частотно-временное распределение.

p, fd, td = pspectrum(x, t, "spectrogram")

instfreq(p, fd, td, out=:plot)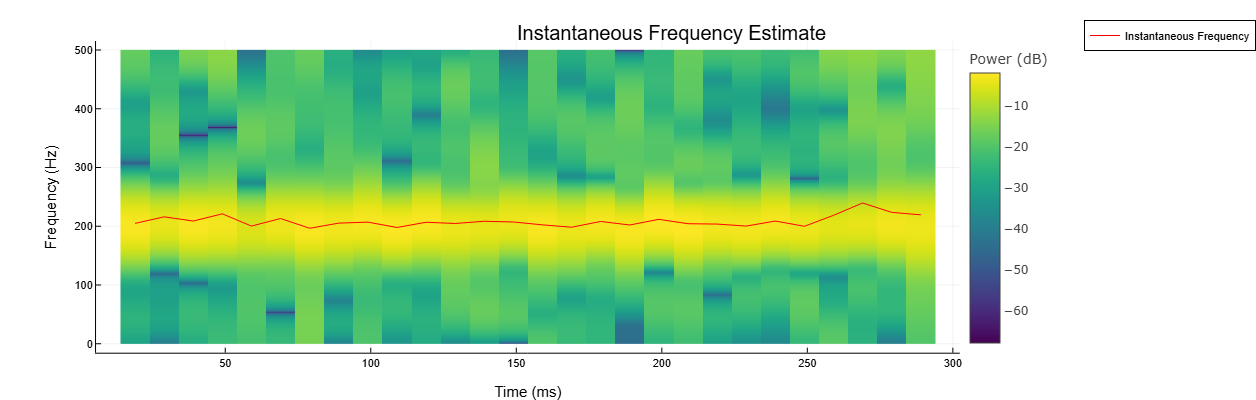

instfreq 9

Дополнительно

Мгновенная частота

Details

Мгновенная частота нестационарного сигнала — это изменяющийся во времени параметр, который относится к среднему значению частот, присутствующих в сигнале по мере его развития [1], [2].

Если для аргумента Method выбрано значение "tfmoment", то функция instfreq оценивает мгновенную частоту как первый условный спектральный момент частотно-временного распределения входного сигнала. Функция:
1. Вычисляет спектр мощности спектрограммы входного сигнала с помощью функции pspectrum и использует спектр в качестве частотно-временного распределения.
2. Оценивает мгновенную частоту с помощью формулы
Если для аргумента Method выбрано значение "hilbert", то функция instfreq оценивает мгновенную частоту как производную фазы аналитического сигнала входного сигнала. Функция:
1. Вычисляет аналитический сигнал входного сигнала с помощью функции hilbert и использует спектр в качестве частотно-временного распределения.
2. Оценивает мгновенную частоту с помощью формулы
  
  где — фаза аналитического сигнала входного сигнала.

Литература

Boashash, Boualem. «Estimating and Interpreting the Instantaneous Frequency of a Signal. I. Fundamentals.» Proceedings of the IEEE^® 80, no. 4 (April 1992): 520–538. https://doi.org/10.1109/5.135376.
Boashash, Boualem. «Estimating and Interpreting The Instantaneous Frequency of a Signal. II. Algorithms and Applications.» Proceedings of the IEEE 80, no. 4 (May 1992): 540–568. https://doi.org/10.1109/5.135378.