Извлечение музыкальных данных

Функции, описанные на этой странице, позволяют упростить извлечение данных из музыкальных записей (в формате MIDI). Отличительной чертой JuliaMusic является функция timeseries, которая позволяет напрямую получать сеточные временные ряды из произвольных структур Notes.

Извлечение основных данных

# MusicManipulations.firstnotes — Function

firstnotes(notes, grid)

Возвращает ноты, которые первыми появляются в каждой точке сетки, не квантуя их.

Эта функция не учитывает ноты по модулю четвертной ноты. У разных четвертных нот разные точки сетки.

# MusicManipulations.filterpitches — Function

filterpitches(notes::Notes, filters) -> newnotes

Сохраняет только те ноты, высота тона которых (одно или несколько значений) указана в filters.

# MusicManipulations.separatepitches — Function

separatepitches(notes::Notes [, allowed])

Возвращает словарь «высота тона» => «ноты этой высоты». При желании можно сохранить только те значения высоты тона, которые содержатся в allowed.

# MusicManipulations.combine — Function

combine(note_container) -> notes

Объединяет заданный контейнер (либо Array{Notes}, либо Dict{Any, Notes}) в один экземпляр Notes. При этом сортирует ноты по их расположению в конечном контейнере.

# MusicManipulations.relpos — Function

relpos(notes::Notes, grid)

Возвращает относительные позиции нот относительно текущей сетки grid, т.е. все ноты приведены в пределах одной четвертной ноты.

Извлечение дополнительных данных

# MusicManipulations.estimate_delay — Function

estimate_delay(notes, grid)

Оценивает среднее временное отклонение заданных нот notes от точки сетки четвертных нот. Ноты классифицируются в соответствии с сеткой grid, и используются только ноты в первом и последнем бинах сетки. Их положение вычитается из соседней четвертной ноты, а возвращаемое значение является средним значением этой операции.

# MusicManipulations.estimate_delay_recursive — Function

estimate_delay_recursive(notes, grid, m)

Делает то же самое, что и estimate_delay, но m раз, на каждом шаге сдвигая ноты на ранее обнаруженную задержку. Это повышает точность алгоритма, так как распределение четвертных нот с каждым разом оценивается все лучше. Как правило, эта функция сходится через несколько m.

Возвращаемый результат представляет собой предполагаемую задержку в виде целого числа (количество импульсов), так как для сдвига нот можно использовать только целые числа.

Временные ряды

# MusicManipulations.timeseries — Function

timeseries(notes::Notes, property::Symbol, f, grid; kwargs...) -> tvec, ts

Генерирует временной ряд свойства property заданных нот, предварительно квантуя по заданной сетке grid (чтобы избежать фактического квантования, используйте сетку 0:1//notes.tpq:1). Возвращает вектор времени tvec в тиках и полученный временной ряд ts.

После квантования многие ноты часто оказываются в одном столбце сетки. Функция f определяет то, какое значение вектора property нот следует сохранить. Типичные значения — minimum, maximum, mean и т. д. Обратите внимание, что столбцы без нот получают значение именованного аргумента missingval, которое по умолчанию равно missing, независимо от функции f или property.

Если property имеет значение :velocity, :pitch или :duration, функция работает в точности так, как описано. property также может иметь значение :position. В этом случае временные ряды ts содержат временные отклонения нот относительно вектора tvec (в литературе эти числа известны как микровременные отклонения).

Если задан именованный аргумент segmented = true, ноты сегментируются в соответствии с сеткой с учетом информации об их длительности; см. описание segment. В противном случае ноты рассматриваются как точечные события без длительности (нет смысла выбирать :duration с segmented).

timeseries(notes::Notes, f, grid) -> tvec, ts

Если property не задано, то f должен принять на вход экземпляр Notes и выдать числовое значение. Это полезно, например, в случаях, когда требуется получить временные ряды скоростей нот самого высокого тона.

Вот пример:

using MusicManipulations, PyPlot, Statistics
midi = readMIDIFile(testmidi())
notes = getnotes(midi, 4)

swung_8s = [0, 2//3, 1]
t, vel = timeseries(notes, :velocity, mean, swung_8s)

notmiss = findall(!ismissing, vel)

fig, (ax1, ax2) = subplots(2,1)
ax1.scatter(t[notmiss], vel[notmiss])
ax1.set_ylabel("velocity")

t, mtd = timeseries(notes, :position, mean, swung_8s)
ax2.scatter(t[notmiss], mtd[notmiss], color = "C1")
ax2.set_ylabel("timing deviations")
ax2.set_xlabel("ticks")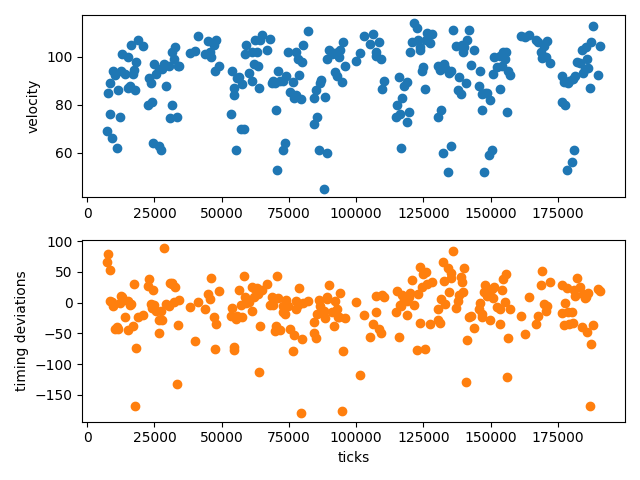

Вот пример кода для получения силы воспроизведения нот с наибольшей высотой тона в каждом сегменте:

notes = getnotes(midi, 4)

function f(notes)
    m, i = findmax(pitches(notes))
    notes[i].velocity
end

grid = 0:1//3:1
tvec2, ts2 = timeseries(notes, f, grid)

Сегментация

# MusicManipulations.segment — Function

segment(notes, grid) → segmented_notes

Quantize the positions and durations of notes and then segment them (i.e. cut them into pieces) according to the duration of a grid unit. This function only works with AbstractRange grids, i.e. equi-spaced grids like 0:1//3:1.

Квантует позиции и длительности нот notes, а затем сегментирует их (т.е. разрезает на части) в соответствии с длительностью единицы сетки. Эта функция работает только с сетками AbstractRange, то есть с сетками с равными интервалами, например 0:1//3:1.