Краткое руководство
Это руководство по началу работы с Plots.jl. Его основная цель — ознакомить вас с терминологией, используемой в пакете, с тем, как использовать Plots.jl в распространенных случаях, и подготовить вас к восприятию остальной части документации. Примеры кода рекомендуется выполнять внутри REPL или в интерактивном скрипте.
Основные принципы построения графиков: линейные графики
Первым шагом после установки Plots.jl с помощью Pkg.add("Plots") является инициализация пакета. В зависимости от компьютера это займет несколько секунд:
using PlotsДля начала построим графики некоторых тригонометрических функций. Для координат x можно создать диапазон от 0 до 10, состоящий, скажем, из 100 элементов. Для координат y можно создать вектор, вычислив sin(x) поэлементно. Для этого в Julia мы вставляем точку сразу после вызова функции. Наконец, мы используем plot() для построения линии.
x = range(0, 10, length=100)
y = sin.(x)
plot(x, y)График отображается в области построения, отдельном окне или браузере, в зависимости от среды и бэкенда (см. ниже).
Если это ваш первый график в сеансе и он появляется не сразу, это нормально. Такая задержка называется проблемой «время до отображения первого графика» (или TTFP). Последующие графики будут появляться быстро. Из-за того, что Julia работает, что называется, «за кадром», решить эту проблему довольно сложно, но за последние несколько лет был достигнут значительный прогресс в сокращении времени компиляции.
В Plots.jl каждый столбец представляет собой ряд — набор связанных точек, образующих линии, поверхности или другие примитивы построения графиков. Мы можем построить несколько линий, начертив матрицу значений, где каждый столбец интерпретируется как отдельная линия. Ниже [y1 y2] формирует матрицу 100x2 (100 элементов, 2 столбца).
x = range(0, 10, length=100)
y1 = sin.(x)
y2 = cos.(x)
plot(x, [y1 y2])Кроме того, можно добавлять дополнительные линии, изменяя объект plot. Для этого используется команда plot!, где ! обозначает, что команда изменяет текущий график. Мы также используем макрос @.. Это вспомогательный макрос, который вставляет точки для каждого вызова функции справа от макроса, гарантируя, что все выражение будет вычисляться поэлементно. Если бы мы вводили точки вручную, для синуса, экспоненты и вычитания их потребовалось бы три, и полученный код был бы менее читабельным.
y3 = @. sin(x)^2 - 1/2 # эквивалентно y3 = sin.(x).^2 .- 1/2
plot!(x, y3)Обратите внимание, что мы могли бы сделать то же самое, что и выше, используя явную переменную графика, которую мы назовем p:
x = range(0, 10, length=100)
y1 = sin.(x)
y2 = cos.(x)
p = plot(x, [y1 y2])
y3 = @. sin(x)^2 - 1/2
plot!(p, x, y3)В тех случаях, когда переменная plot опущена, Plots.jl автоматически использует глобальную переменную Plots.CURRENT_PLOT.
Сохранение фигур
Сохранение графиков выполняется с помощью команды savefig. Например:
savefig("myplot.png") # сохраняет CURRENT_PLOT в PNG-формате
savefig(p, "myplot.pdf") # сохраняет график из p в виде векторной графики в PDF-форматеСуществуют также вспомогательные функции png, Plots.pdf и другие неэкспортируемые вспомогательные методы. При их использовании расширение опускается из имени файла. Следующий фрагмент эквивалентен приведенному выше коду:
png("myplot")
Plots.pdf(p, "myplot")Дополнительные сведения о выводе фигур можно найти в разделе Вывод данного руководства.
Атрибуты графика
В предыдущем разделе мы строили графики. И с ними мы закончили, верно? Нет. Графики необходимо стилистически оформить. В Plots.jl модификаторы графиков называются атрибутами, которые приведены на странице атрибутов. При работе с данными и атрибутами в Plots.jl соблюдаются два простых правила:
-
Позиционные аргументы соответствуют входным данным
-
Именованные аргументы соответствуют атрибутам
Так, например, plot(x, y, z) — это трехмерные данные для трехмерных графиков без атрибутов, а plot(x, y, attribute=value) — это двухмерные данные с одним атрибутом, которому присвоено некоторое значение.
В качестве примера можно привести изменение ширины линии с помощью linewidth (или его псевдонима lw), изменение надписей условных обозначений с помощью label и добавление названия с помощью title. Обратите внимание, что ["sin(x)" "cos(x)"] имеет столько же столбцов, сколько и данные. Кроме того, поскольку ширина строки приписывается к [y1 y2], обе строки будут затронуты присвоенным значением. Применим все это к предыдущему графику:
x = range(0, 10, length=100)
y1 = sin.(x)
y2 = cos.(x)
plot(x, [y1 y2], title="Trigonometric functions", label=["sin(x)" "cos(x)"], linewidth=3)Каждый атрибут может быть также применен путем изменения графика с помощью функции-модификатора. Некоторые атрибуты имеют собственные специальные функции-модификаторы, другие доступны через plot!(attribute=value). Например, атрибут xlabel добавляет надпись для оси x. Мы можем указать его в команде plot с помощью xlabel=..., а можем воспользоваться функцией-модификатором, приведенным ниже, чтобы добавить его после того, как график уже будет сгенерирован. Что лучше для читаемости кода — решать вам.
xlabel!("x")Каждая функция-модификатор представляет собой имя атрибута, за которым следует !. При этом неявным образом будет использоваться глобальная переменная Plots.CURRENT_PLOT. Ее можно применить другим объектам графика с помощью attribute!(p, value), где p — имя объекта графика, который необходимо изменить.
Мы будем использовать ключевые слова и функции-модификаторы как взаимозаменяемые для выполнения некоторых общих изменений примера, приведенного ниже. Можно заметить, что для атрибутов ls и legend значения содержат двоеточие :. Двоеточие обозначает символ в Julia. Двоеточия широко используются для значений атрибутов в Plots.jl, наряду со строками и числами.
-
Надписи для отдельных линий, отображаемые в условных обозначениях
-
Ширина линий (мы будем использовать псевдоним
lwвместоlinewidth) -
Стили линий (мы будем использовать псевдоним
lsвместоlinestyle) -
Положение условных обозначений (вне графика, так как стандартное положение будет загромождать график)
-
Столбцы условных обозначений (3, для лучшего использования горизонтального пространства)
-
X-ограничения для перехода от
0к2pi -
Название графика и метки осей
x = range(0, 10, length=100)
y1 = sin.(x)
y2 = cos.(x)
y3 = @. sin(x)^2 - 1/2
plot(x, [y1 y2], label=["sin(x)" "cos(x)"], lw=[2 1])
plot!(x, y3, label="sin(x)^2 - 1/2", lw=3, ls=:dot)
plot!(legend=:outerbottom, legendcolumns=3)
xlims!(0, 2pi)
title!("Trigonometric functions")
xlabel!("x")
ylabel!("y")Обратите внимание, что y3 строится в виде пунктирной линии. В этом отличие от графика рассеяния данных.
Графики с логарифмической шкалой
Иногда требуется построить график данных по порядку величины. В этом случае атрибутам xscale и yscale можно задать значение :log10. Им также можно задать :identity для сохранения линейного масштаба. Необходимо следить за тем, чтобы значения данных и ограничений были положительными.
x = 10 .^ range(0, 4, length=100)
y = @. 1/(1+x)
plot(x, y, label="1/(1+x)")
plot!(xscale=:log10, yscale=:log10, minorgrid=true)
xlims!(1e+0, 1e+4)
ylims!(1e-5, 1e+0)
title!("Log-log plot")
xlabel!("x")
ylabel!("y")Дополнительные сведения об атрибутах можно найти в разделе Вывод данного руководства.
Строки уравнений LaTeX
Plots.jl работает с пакетом LaTeXStrings.jl, который позволяет пользователю вводить уравнения LaTeX в строковых литералах. Для его установки введите Pkg.add("LaTeXStrings"). Самым простым способом его использования является добавление L в начало отформатированной строки LaTeX. Если строка представляет собой сочетание обычного текста и уравнений LaTeX, при необходимости вставьте знаки доллара $.
using LaTeXStrings
x = 10 .^ range(0, 4, length=100)
y = @. 1/(1+x)
plot(x, y, label=L"\frac{1}{1+x}")
plot!(xscale=:log10, yscale=:log10, minorgrid=true)
xlims!(1e+0, 1e+4)
ylims!(1e-5, 1e+0)
title!(L"Log-log plot of $\frac{1}{1+x}$")
xlabel!(L"x")
ylabel!(L"y")Изменение типа ряда: графики рассеяния
На данный момент вы уже знаете о линейных графиках, но не хотите ли вы построить график данных другим способом? В Plots.jl эти другие способы построения ряда называются типом ряда. Линия является одним из типов рядов. Однако еще одним широко используемым видом рядов является график рассеяния.
Начнем с функции синуса, но на этот раз определим вектор y_noisy, который вносит некоторую случайность. Можно изменить тип ряда с помощью атрибута seriestype.
x = range(0, 10, length=100)
y = sin.(x)
y_noisy = @. sin(x) + 0.1*randn()
plot(x, y, label="sin(x)")
plot!(x, y_noisy, seriestype=:scatter, label="data")Для каждого встроенного типа ряда существует сокращенная функция прямого вызова этого типа ряда, соответствующая его имени. Она работает с атрибутами так же, как команда plot, и имеет изменяемую форму, которая заканчивается на !. Например, можно записать последнюю линию следующим образом:
scatter!(x, y_noisy, label="data")Доступные типы рядов зависят от бэкенда и приведены на странице Поддерживаемые атрибуты. Как будет описано далее, другие библиотеки могут добавлять новые типы рядов, используя шаблоны.
Графики рассеяния будут иметь некоторые общие атрибуты, связанные с маркерами. Вот пример того же графика, но с некоторыми атрибутами, придающими графику более презентабельный вид. Многие псевдонимы используются для краткости, и приведенный ниже список не является исчерпывающим.
-
lcдляlinecolor -
lwдляlinewidth -
mcдляmarkercolor -
msдляmarkersize -
maдляmarkeralpha
x = range(0, 10, length=100)
y = sin.(x)
y_noisy = @. sin(x) + 0.1*randn()
plot(x, y, label="sin(x)", lc=:black, lw=2)
scatter!(x, y_noisy, label="data", mc=:red, ms=2, ma=0.5)
plot!(legend=:bottomleft)
title!("Sine with noise")
xlabel!("x")
ylabel!("y")Бэкенды построения графиков
Plots.jl — это метапакет для построения графиков: он представляет собой интерфейс для множества различных библиотек для построения графиков. На самом деле Plots.jl интерпретирует ваши команды, а затем строит графики с помощью другой библиотеки построения графиков, называемой бэкендом. Что хорошо, так это то, что вы можете применять множество различных библиотек для построения графиков, используя синтаксис Plots.jl, и в скором времени мы увидим, что Plots.jl добавляет новые возможности в каждую из этих библиотек.
Когда мы начали строить график выше, для него использовался бэкенд GR по умолчанию. Однако, допустим, нам нужен другой бэкенд для построения графиков, который будет выводить графики в красивый графический интерфейс или в панель построения в VS Code. Для этого потребуется бэкенд, совместимый с перечисленными возможностями. Распространенными бэкендами для выполнения этих задач являются PythonPlot и Plotly. Например, чтобы установить PythonPlot, достаточно ввести в REPL команду Pkg.add("PythonPlot"). Чтобы установить Plotly, введите Pkg.add("PlotlyJS").
Можно специально выбрать бэкенд, в который выполняется построение графика, используя в качестве функции имя бэкенда в нижнем регистре. Построим график примера, приведенного выше, с помощью Plotly, а затем — GR:
plotlyjs() # задает Plotly в качестве бэкенда
x = range(0, 10, length=100)
y = sin.(x)
y_noisy = @. sin(x) + 0.1*randn()
# выполняется построение в отдельное окно с помощью Plotly
plot(x, y, label="sin(x)", lc=:black, lw=2)
scatter!(x, y_noisy, label="data", mc=:red, ms=2, ma=0.5)
plot!(legend=:bottomleft)
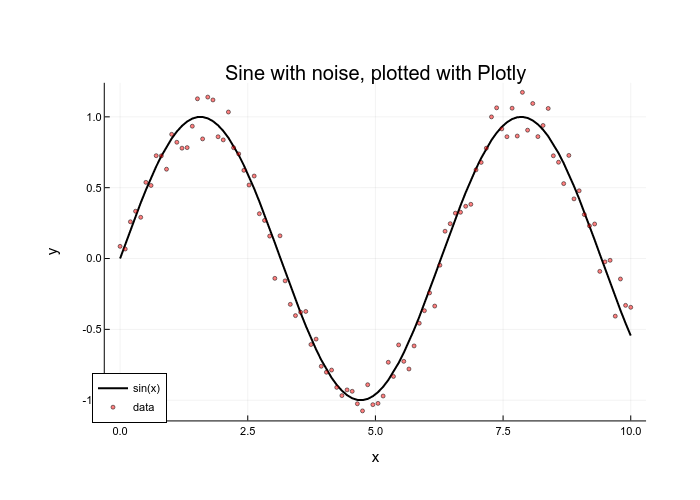
title!("Sine with noise, plotted with Plotly")
xlabel!("x")
ylabel!("y")"plotlyjs_tutorial.png"
gr() # задает GR в качестве бэкенда
# выполняется построение с помощью GR
plot(x, y, label="sin(x)", lc=:black, lw=2)
scatter!(x, y_noisy, label="data", mc=:red, ms=2, ma=0.5)
plot!(legend=:bottomleft)
title!("Sine with noise, plotted with GR")
xlabel!("x")
ylabel!("y")Каждый бэкенд построения графиков имеет свои особенности. Некоторые из них обладают интерактивностью, некоторые работают быстрее и могут обрабатывать огромное количество точек данных, а некоторые могут создавать трехмерные графики. Одни бэкенды, например GR, могут осуществлять сохранение в векторную графику и PDF-файлы, а другие, например Plotly, — только в PNG.
Дополнительные сведения о бэкендах см. на этой странице. Примеры графиков, полученных с помощью различных бэкендов, приведены в разделе «Примеры».
Построение графиков с помощью скриптов
В начале руководства мы рекомендовали выполнять примеры кода в интерактивном сеансе по следующей причине: попробуйте добавить эти же команды построения в скрипт. Теперь вызовите скрипт… А график не появляется? Это связано с тем, что Julia при интерактивном использовании через REPL вызывает display для каждой переменной, возвращаемой командой без точки с запятой ;. В каждом из приведенных случаев интерактивное использование заключалось в автоматическом вызове display для возвращаемых объектов графика.
В скрипте Julia не выполняет автоматические отображения, поэтому ; не требуется. Однако если нужно отобразить графики в скрипте, это означает, что достаточно добавить вызов display. Например:
display(plot(x, y))Или же можно вызвать gui() в конце, чтобы сделать то же самое. Наконец, если у нас есть объект графика p, можно ввести display(p) для отображения графика.
Объединение нескольких графиков в виде подграфиков
Объединить несколько графиков в виде подграфиков можно с помощью макетов. Для этого существует множество методов, и мы рассмотрим два простых метода создания простых макетов. Более сложные макеты представлены на странице Макеты.
Первый метод заключается в определении макета, который будет разделять ряды. Команда layout принимает 2-местный кортеж layout=(N, M), который строит сетку графиков NxM, и автоматически разбивает ряды так, чтобы ряд находился в каждом графике. Например, если на графике с тремя рядами ввести layout=(3, 1), мы получим три строки графиков, в каждом из которых будет по одному ряду.
Определим некоторые функции и построим их на отдельных графиках. Поскольку на каждом графике имеется только один ряд, мы также удалим условные обозначения на каждом из графиков с помощью legend=false.
x = range(0, 10, length=100)
y1 = @. exp(-0.1x) * cos(4x)
y2 = @. exp(-0.3x) * cos(4x)
y3 = @. exp(-0.5x) * cos(4x)
plot(x, [y1 y2 y3], layout=(3, 1), legend=false)Мы также можем использовать макеты на графиках объектов графика. Например, можно сгенерировать четыре отдельных графика и создать один график, объединяющий их в сетку 2х2.
x = range(0, 10, length=100)
y1 = @. exp(-0.1x) * cos(4x)
y2 = @. exp(-0.3x) * cos(4x)
y3 = @. exp(-0.1x)
y4 = @. exp(-0.3x)
y = [y1 y2 y3 y4]
p1 = plot(x, y)
p2 = plot(x, y, title="Title 2", lw=3)
p3 = scatter(x, y, ms=2, ma=0.5, xlabel="xlabel 3")
p4 = scatter(x, y, title="Title 4", ms=2, ma=0.2)
plot(p1, p2, p3, p4, layout=(2,2), legend=false)Обратите внимание, что атрибуты в отдельных графиках применяются к этим отдельным графикам, в то время как атрибут legend=false в заключительном вызове plot применяется ко всем подграфикам.
Шаблоны графиков и библиотеки шаблонов
Теперь вы знаете всю основную терминологию Plots.jl и можете свободно просматривать документацию, чтобы в дальнейшем стать мастером построения графиков. Однако кое-что осталось: шаблоны. Шаблоны построения графиков являются расширениями платформы Plots.jl. Они добавляют следующие компоненты.
-
Новые команды
plotпосредством шаблонов пользователей. -
Интерпретации типов Julia по умолчанию как данные построения графиков посредством шаблонов типов.
-
Новые функции для создания графиков с помощью шаблонов графиков.
-
Новые типы рядов с помощью шаблонов рядов.
Создание собственных шаблонов является дополнительной темой, описанной на странице шаблонов. Здесь мы представим способы использования шаблона.
Шаблоны входят во многие библиотеки шаблонов. Две фундаментальные библиотеки шаблонов — это PlotRecipes.jl и StatsPlots.jl. Рассмотрим StatsPlots.jl. StatsPlots.jl добавляет множество шаблонов, но мы остановимся только на некоторых.
-
Шаблон типа для распределений (
Distribution). -
Шаблон графика для граничных гистограмм.
-
Множество новых рядов статистических графиков.
Кроме шаблонов, StatsPlots.jl предоставляет специализированный макрос @df для построения графиков непосредственно из таблиц данных.
Использование пользовательских шаблонов
Пользовательский шаблон указывает, как интерпретировать команды построения графиков для нового типа данных. В этом случае в StatsPlots.jl есть макрос @df, позволяющий строить график DataFrame непосредственно с использованием имен столбцов. Давайте построим DataFrame со столбцами a, b и c и укажем Plots.jl использовать a в качестве оси x и построить ряд, заданный столбцами b и c:
# Pkg.add("StatsPlots")
# требуется для пользовательского шаблона dataframe
using StatsPlots
# создадим dataframe
using DataFrames
df = DataFrame(a=1:10, b=10*rand(10), c=10*rand(10))
# строит dataframe путем объявления точек по именам столбцов
# x = :a, y = [:b :c] (обратите внимание, что y имеет два столбца!)
@df df plot(:a, [:b :c])Объем работы здесь небольшой: все команды, использовавшиеся ранее (атрибуты, типы рядов и т. д.), по-прежнему будут работать с этими данными:
# x = :a, y = :b
@df df scatter(:a, :b, title="My DataFrame Scatter Plot!")Использование шаблона типа
Кроме того, StatsPlots.jl расширяет Distributions.jl, добавляя шаблон типа для своих типов распределений, так что они могут быть непосредственно интерпретированы как данные для построения графиков:
using Distributions
plot(Normal(3, 5), lw=3)Шаблоны типов очень удобно использовать для построения специализированного типа, который не требует дополнительного вмешательства.
Использование шаблонов графиков
StatsPlots.jl добавляет несколько графиков marginhist с помощью шаблона графика. В качестве данных возьмем известный набор данных iris из RDatasets:
# Pkg.add("RDatasets")
using RDatasets, StatsPlots
iris = dataset("datasets", "iris")
@df iris marginalhist(:PetalLength, :PetalWidth)Здесь iris — это DataFrame. Используя макрос @df для DataFrame, описанный выше, мы передаем marginalhist(x, y) данные из столбцов PetalLength и PetalWidth.
Обратите внимание, что это не просто ряд, поскольку генерируется несколько рядов (т. е. имеется несколько графиков из-за гистограмм сверху и справа). Таким образом, шаблон графика — это не просто ряд, но и нечто вроде новой команды plot.
Использование шаблонов рядов
В StatsPlots.jl также доступны новые шаблоны рядов. Главное, что не нужно ничего менять. После using StatsPlots можно просто использовать эти новые шаблоны рядов, как если бы они были встроены в библиотеки построения графиков. Будем использовать график «Скрипка» с некоторыми случайными данными:
y = rand(100, 4)
violin(["Series 1" "Series 2" "Series 3" "Series 4"], y, legend=false)Можно добавить boxplot сверху, используя те же команды изменения, что и раньше:
boxplot!(["Series 1" "Series 2" "Series 3" "Series 4"], y, legend=false)Дополнительные надстройки, которые можно попробовать
Учитывая легкую расширяемость Plots.jl, можно попробовать и многие другие инструменты. Вот краткий список очень полезных надстроек, с которыми стоит ознакомиться:
-
PlotThemes.jl позволяет изменять цветовую схему графиков. Например,
theme(:dark)добавляет темную тему. -
StatsPlots.jl добавляет функциональность для визуализации статистического анализа.
-
Множество других пакетов, имеющих шаблоны и расширяющих функциональность Plots.jl, представлено на странице «Экосистема».