Heat Exchanger (TL)

Heat exchanger for systems with heat-conducting liquid flow and controlled flow.

blockType: EngeeFluids.HeatExchangers.EffectivenessNTU.ThermalLiquid

Path in the library:

/Physical Modeling/Fluids/Heat Exchangers/Thermal Liquid/Heat Exchanger (TL)

Description

Block Heat Exchanger (TL) simulates the cooling and heating of liquids through thermal conduction through a thin wall. The properties of a single-phase thermally conductive liquid are set on the tab Thermal Liquid. The second coolant is adjustable, and its properties are set only by the parameters on the tab Controlled Fluid. It does not get any properties from the liquid domain network. Heat exchange between heat carriers is based on contact heat exchange with a heat-conducting liquid.

heat exchanger g g 1

The heat transfer model

The block’s heat transfer model is based on the "efficiency-number of heat transfer units" (E-NTU) method. In steady-state mode, heat exchange is carried out with an efficiency equal to only a fraction of the ideal value, which is achievable in the absence of thermal resistance and constant temperatures at the flow inlet.:

where

— actual heat flow;
— perfect heat flow;
— the efficiency of the heat exchanger, which is based on the ratio of flow heat capacities and the number of transfer units :

where
- — total thermal resistance, for more information, see Thermal resistance;
- — the lower of the values of the flow heat capacity for two heat carriers;
- — the larger of the values of the flow heat capacity for two heat carriers.

The flow heat capacity depends on the specific heat capacity of the coolant ( ) and from its mass flow through the heat exchanger ( ):

Efficiency also depends on the relative position of the streams, the number of strokes between them, and the mixing conditions of the streams. Each coolant flow pattern uses its own efficiency expression. The list of such expressions is given in the block E-NTU Heat Transfer.

Flow diagram of heat carriers

Parameter Flow arrangement defines the mutual direction of flows: direct flow, countercurrent, across each other (transverse), as well as the "pipe in a casing" design, in which one flow passes inside the pipes and the other outside, in the casing. The figure below illustrates this flow pattern. The flow in the pipes can make either one stroke through the casing (Fig. on the right) or several strokes (Fig. on the left) for greater heat exchange efficiency.

heat exchanger g g 2

Alternative flow patterns of heat carriers can be set by general parameterization with tabular efficiency data, which does not require a detailed specification of the heat exchanger. Such data should reflect the flow pattern of the heat carriers, the degree of their mixing, and the number of passages through the casing or pipe.

Mixing condition

Parameter Cross flow type allows you to set the mixing pattern: one of the streams is mixed, both or none. Mixing involves the transverse movement of the coolant in channels devoid of internal barriers (guides, partitions, ribs or walls). It helps to equalize the temperature gradients in the cross-section. In unmixed streams, as shown in the figure below on the right, the temperature changes only along the flow direction, in mixed streams (Fig. on the left) — both longitudinally and transversely.

heat exchanger g g 3 en

The difference between mixed and unmixed flows is taken into account only in the flow patterns of heat carriers with transverse flows, where a longitudinal change in the temperature of one coolant induces transverse temperature gradients in the other. In schemes with direct-flow/countercurrent movement of heat carriers, only longitudinal changes in the temperature of the heat carriers occur and mixing practically does not affect heat transfer, therefore it is not taken into account.

Efficiency curves

Shell-and-tube multi-pass heat exchangers are the most effective (iv.b-e in the figure for 2, 3 and 4 passages). Among single-stroke heat exchangers, countercurrent heat exchangers (ii) are the most efficient, while direct-flow heat exchangers (i) are the least efficient.

Cross-flow heat exchangers occupy an intermediate position in terms of efficiency and their efficiency depends on the degree of mixing. The highest is achieved when there is no mixing in both streams (iii.a), the lowest is achieved when both are mixed (iii.b). Mixing only the stream with the lowest flow heat capacity (iii.c) reduces efficiency to a greater extent than mixing the stream with the highest flow heat capacity (iii.d).

heat exchanger g g 4

Thermal resistance

Total thermal resistance It represents the sum of local resistances in the direction of heat transfer. These include: convection on the wall surface and thermal conduction through the wall and contaminated layers in the presence of deposits. The formula below is used to calculate the total resistance in the direction from a thermally conductive liquid to a regulated coolant:

where

— the coefficient of convective heat transfer between the heat-conducting liquid and the wall;
— coefficients of convective heat transfer between the regulated coolant and the wall, which enters the port as a scalar HC2;
— the coefficient of deposits on the wall from the side of the heat-conducting liquid, the value of the parameter Fouling factor;
— the coefficient of deposits on the wall from the side of the regulated coolant, the value of the parameter Fouling factor;
— the surface area of heat transfer from the side of the heat-conducting liquid, the value of the parameter Heat transfer surface area;
— the surface area of the heat transfer from the side of the regulated coolant, the value of the parameter Heat transfer surface area;
— thermal resistance of the wall, parameter value Wall thermal resistance.

heat exchanger g g 5 en

The heat transfer coefficients depend on the configuration of the heat exchanger and the properties of the liquid. For more information, see the section E-NTU Heat Transfer.

Block structure

A block is a composite component built from simpler blocks.: Heat Exchanger Interface (TL) and E-NTU Heat Transfer.

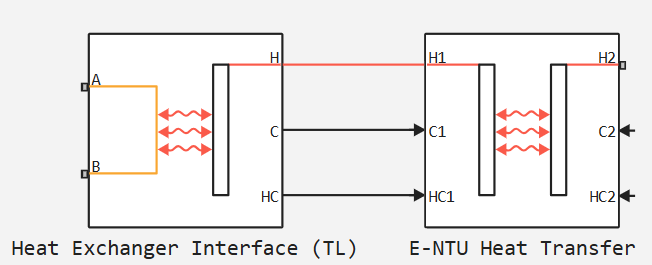
heat exchanger tl engee

Ports

Conserving

# A1 — thermal liquid inlet or outlet
thermal liquid

Details

Inlet or outlet port for thermal liquid on the corresponding side of the heat exchanger.

Program usage name

thermal_liquid_port_a1

# B1 — thermal liquid inlet or outlet
thermal liquid

Details

Inlet or outlet port for thermal liquid on the corresponding side of the heat exchanger.

Program usage name

thermal_liquid_port_b1

# H2 — inlet temperature of the regulated heat transfer fluid
`heat

Details

Non-directional port related to the inlet temperature of the regulated heat transfer fluid.

Program usage name

thermal_port2

Input

# C2 — flow heat capacity of the regulated coolant
scalar

Details

Input port that receives the value of the flow heat capacity of the regulated coolant.

Data types	`Float64`.
Complex numbers support	No

# HC2 — heat transfer coefficient of the regulated coolant
scalar

Details

Heat transfer coefficient between the regulated fluid and the separating wall.

Data types	`Float64`.
Complex numbers support	No

Parameters

Common

# Flow arrangement — flow diagram of heat carriers in the heat exchanger
Parallel or counter flow | Shell and tube | Cross flow | Generic - effectiveness table

Details

The parameter that defines the relative arrangement of the flows in the heat exchanger: direct flow, countercurrent, across each other (transverse), as well as the "pipe in the casing" design, in which one flow passes inside the pipes and the other outside, in the casing.

Alternative flow patterns of heat carriers can be specified in an arbitrary efficiency table, which does not require detailed specifications of the heat exchanger.

Values	`Parallel or counter flow` \| `Shell and tube` \| `Cross flow` \| `Generic - effectiveness table`
Default value	`Parallel or counter flow`
Program usage name	`flow_arrangement_type`
Evaluatable	No

# Wall thermal resistance — wall resistance to heat flow due to thermal conductivity
K/W

Details

The resistance of the wall to heat flow due to thermal conductivity and the inverse of thermal conductivity, or the product of thermal conductivity by the ratio of surface area to length. The wall resistance is combined with convective resistance and sediment resistance to determine the overall heat transfer coefficient between the flows.

Units	`K/W`
Default value	`0.00016 K/W`
Program usage name	`R_wall`
Evaluatable	Yes

Thermal Liquid

# Minimum free-flow area — the cross-sectional area of the channel at its narrowest point
m^2 | um^2 | mm^2 | cm^2 | km^2 | in^2 | ft^2 | yd^2 | mi^2 | ha | ac

Details

The minimum cross-sectional area of the channel through which the coolant flows between the inlet and outlet. If it is a set of channels, tubes, slits, or grooves, then the value of the parameter is defined as the sum of the smallest areas at the point of the minimum flow area.

Units	`m^2` \| `um^2` \| `mm^2` \| `cm^2` \| `km^2` \| `in^2` \| `ft^2` \| `yd^2` \| `mi^2` \| `ha` \| `ac`
Default value	`0.01 m^2`
Program usage name	`min_flow_area_1`
Evaluatable	Yes

# Hydraulic diameter for pressure loss — the hydraulic diameter of the channel at its narrowest point
m | um | mm | cm | km | in | ft | yd | mi | nmi

Details

The effective internal diameter of the channel in the section with the smallest area. For non—circular channels, the hydraulic diameter is the equivalent diameter of a circle with an area equal to the area of the existing channel. Its value is equal to the ratio of the minimum cross-sectional area of the channel to a quarter of its total perimeter.

If a channel is defined by a set of channels, pipes, slots, or grooves, then the total perimeter is equal to the sum of the perimeters of all the elements. If the channel is a round pipe, then its hydraulic diameter is equal to the actual one.

Units	`m` \| `um` \| `mm` \| `cm` \| `km` \| `in` \| `ft` \| `yd` \| `mi` \| `nmi`
Default value	`0.1 m`
Program usage name	`hydraulic_diameter_for_pressure_loss_1`
Evaluatable	Yes

# Thermal Liquid volume — the total volume of the coolant in the channel of the heat-conducting liquid
m^3 | um^3 | mm^3 | cm^3 | km^3 | ml | l | gal | igal | in^3 | ft^3 | yd^3 | mi^3

Details

The total volume of the coolant contained in the channel of the heat-conducting liquid.

Units	`m^3` \| `um^3` \| `mm^3` \| `cm^3` \| `km^3` \| `ml` \| `l` \| `gal` \| `igal` \| `in^3` \| `ft^3` \| `yd^3` \| `mi^3`
Default value	`0.01 m^3`
Program usage name	`V_liquid_1`
Evaluatable	Yes

# Laminar flow upper Reynolds number limit — the lower boundary of the transition zone between laminar and turbulent flow regimes

Details

The value of the Reynolds number corresponding to the lower boundary of the transition zone between laminar and turbulent flow regimes. Above this value, inertial forces begin to dominate, as a result of which the flow passes from laminar to turbulent mode. The default value corresponds to a round tube with a smooth inner surface.

Default value	`2000.0`
Program usage name	`Re_laminar_1`
Evaluatable	Yes

# Turbulent flow lower Reynolds number limit — the upper boundary of the transition zone between laminar and turbulent flow regimes

Details

The value of the Reynolds number corresponding to the upper boundary of the transition zone between laminar and turbulent flow regimes. Below this value, viscous forces begin to dominate, as a result of which the flow passes from a turbulent to a laminar regime. The default value corresponds to a round tube with a smooth inner surface.

Default value	`4000.0`
Program usage name	`Re_turbulent_1`
Evaluatable	Yes

# Pressure loss model — mathematical model for calculating pressure losses due to viscous friction
Pressure loss coefficient | Correlation for flow inside tubes | Tabulated data - Darcy friction factor vs. Reynolds number | Tabulated data - Euler number vs. Reynolds number

Details

This parameter allows you to select one of the models for calculating pressure losses due to viscous friction. The parameter determines which expressions will be used in calculating losses, as well as which block parameters must be set at the input. The details of the calculations, depending on the chosen parameterization, are given in the block Heat Exchanger Interface (TL).

Values	`Pressure loss coefficient` \| `Correlation for flow inside tubes` \| `Tabulated data - Darcy friction factor vs. Reynolds number` \| `Tabulated data - Euler number vs. Reynolds number`
Default value	`Pressure loss coefficient`
Program usage name	`pressure_loss_type_1`
Evaluatable	No

# Pressure loss coefficient — total coefficient that takes into account hydraulic losses between ports

Details

The total loss coefficient takes into account all hydraulic flow resistances in the channel, including wall friction losses (major losses) and local resistances due to bends, bends and other geometry changes (minor losses).

The loss coefficient is an empirical dimensionless quantity widely used to describe pressure losses caused by viscous friction. It can be calculated based on experimental data or, in some cases, obtained from technical documentation.

Dependencies

To use this parameter, set for the parameter Pressure loss model meaning Pressure loss coefficient.

Default value	`0.1`
Program usage name	`pressure_loss_coefficient_1`
Evaluatable	Yes

# Heat transfer coefficient model — mathematical model for heat exchange between a heat carrier and a wall
Constant heat transfer coefficient | Correlation for flow inside tubes | Tabulated data - Colburn factor vs. Reynolds number | Tabulated data - Nusselt number vs. Reynolds number and Prandtl number

Details

A mathematical model for heat transfer between a heat carrier and a wall. The choice of the model determines which expressions to use and which parameters to specify for heat transfer calculations.

For more information, see the section E-NTU Heat Transfer.

Values	`Constant heat transfer coefficient` \| `Correlation for flow inside tubes` \| `Tabulated data - Colburn factor vs. Reynolds number` \| `Tabulated data - Nusselt number vs. Reynolds number and Prandtl number`
Default value	`Constant heat transfer coefficient`
Program usage name	`heat_transfer_type_1`
Evaluatable	No

# Heat transfer surface area — the effective surface area used in heat transfer between the heat carrier and the wall
m^2 | um^2 | mm^2 | cm^2 | km^2 | in^2 | ft^2 | yd^2 | mi^2 | ha | ac

Details

The effective surface area used in heat transfer between the heat carrier and the wall. The effective surface area is the sum of the primary and secondary surface areas, the area on which the wall is exposed to the liquid, and the area of the ribs, if any. The surface area of the ribs is usually calculated by the efficiency coefficient of the ribs.

Units	`m^2` \| `um^2` \| `mm^2` \| `cm^2` \| `km^2` \| `in^2` \| `ft^2` \| `yd^2` \| `mi^2` \| `ha` \| `ac`
Default value	`0.4 m^2`
Program usage name	`heat_transfer_area_1`
Evaluatable	Yes

# Liquid-wall heat transfer coefficient — coefficient of heat transfer during convection between a heat-conducting liquid and a wall
W/(m^2*K) | Btu_IT/(hr*ft^2*deltadegR)

Details

The heat transfer coefficient for convection between the gas and the wall. The resistance caused by deposits is taken into account separately in the parameter Fouling factor.

Dependencies

To use this parameter, set for the parameter Heat transfer coefficient model meaning Constant heat transfer coefficient.

Units	`W/(m^2K)` \| `Btu_IT/(hrft^2*deltadegR)`
Default value	`100.0 W/(m^2*K)`
Program usage name	`alpha_const_1`
Evaluatable	Yes

# Fouling factor — thermal resistance due to deposits
K*m^2/W | deltadegR*ft^2*hr/Btu_IT

Details

Thermal resistance due to deposits that form over time on the exposed wall surfaces. Deposits, because they create a new solid layer between the coolant and the wall through which heat must pass, add additional thermal resistance to the heat transfer path. Deposits grow slowly, and the resistance caused by them is assumed to be constant during the simulation.

Units	`Km^2/W` \| `deltadegRft^2*hr/Btu_IT`
Default value	`0.0001 K*m^2/W`
Program usage name	`fouling_factor1`
Evaluatable	Yes

# Minimum fluid-wall heat transfer coefficient — lower bound for the gas heat transfer coefficient
W/(m^2*K) | Btu_IT/(hr*ft^2*deltadegR)

Details

The lower bound for the heat transfer coefficient between the gas and the wall. If the calculation gives a lower heat transfer coefficient, then the value Minimum fluid-wall heat transfer coefficient replaces the calculated value.

Units	`W/(m^2K)` \| `Btu_IT/(hrft^2*deltadegR)`
Default value	`5.0 W/(m^2*K)`
Program usage name	`alpha1_min`
Evaluatable	Yes

Controlled Fluid

Details

Units	`m^2` \| `um^2` \| `mm^2` \| `cm^2` \| `km^2` \| `in^2` \| `ft^2` \| `yd^2` \| `mi^2` \| `ha` \| `ac`
Default value	`0.4 m^2`
Program usage name	`heat_transfer_area_2`
Evaluatable	Yes

# Fouling factor — thermal resistance due to deposits
K*m^2/W | deltadegR*ft^2*hr/Btu_IT

Details

Units	`Km^2/W` \| `deltadegRft^2*hr/Btu_IT`
Default value	`0.0001 K*m^2/W`
Program usage name	`fouling_factor2`
Evaluatable	Yes

# Minimum fluid-wall heat transfer coefficient — the lower limit for the heat transfer coefficient of the regulated coolant
W/(m^2*K) | Btu_IT/(hr*ft^2*deltadegR)

Details

The lower limit for the heat transfer coefficient between the coolant and the wall. If the calculation gives a lower heat transfer coefficient, then the value Minimum fluid-wall heat transfer coefficient replaces the calculated value.

Units	`W/(m^2K)` \| `Btu_IT/(hrft^2*deltadegR)`
Default value	`5.0 W/(m^2*K)`
Program usage name	`alpha2_min`
Evaluatable	Yes

Effects and Initial Conditions

# Thermal Liquid 1 dynamic compressibility — compressibility of a heat-conducting liquid in a heat exchanger

Details

An option for simulating pressure changes inside the heat exchanger. If this option is unchecked, then the pressure derivatives are not taken into account in the equations of conservation of energy and mass. The pressure inside the heat exchanger is defined as the average of the two port pressures.

Default value	`true (switched on)`
Program usage name	`dynamic_compressibility_1`
Evaluatable	No

Details

The temperature of the heat-conducting liquid in the channel at the beginning of the simulation.

Units	`K` \| `degC` \| `degF` \| `degR` \| `deltaK` \| `deltadegC` \| `deltadegF` \| `deltadegR`
Default value	`293.15 K`
Program usage name	`T_start_1`
Evaluatable	Yes

# Thermal Liquid initial pressure — the pressure of the heat-conducting liquid in the channel at the beginning of the simulation
Pa | uPa | hPa | kPa | MPa | GPa | kgf/m^2 | kgf/cm^2 | kgf/mm^2 | mbar | bar | kbar | atm | ksi | psi | mmHg | inHg

Details

The pressure of the heat-conducting liquid in the channel at the beginning of the simulation.

Units	`Pa` \| `uPa` \| `hPa` \| `kPa` \| `MPa` \| `GPa` \| `kgf/m^2` \| `kgf/cm^2` \| `kgf/mm^2` \| `mbar` \| `bar` \| `kbar` \| `atm` \| `ksi` \| `psi` \| `mmHg` \| `inHg`
Default value	`0.101325 MPa`
Program usage name	`p_start_1`
Evaluatable	Yes