decimate

Decimation is a decrease in the sampling rate by an integer number of times.

Library

EngeeDSP

Syntax

Function call

y = decimate(x, r, mode) — reduces the sampling rate of the input signal x in r once. Signal output signal y shortened to r once: length(y) = ceil(length(x)/r). It uses an FIR filter with a finite impulse response, developed using a Hamming window. The filter has an order 30.

y = decimate(x, r) — function decimate uses an IIR Chebyshev filter of the 8th order.

y = decimate(x, r, n, mode) — uses a FIR filter designed using a Hamming window. The filter has an order n.

y = decimate(x, r, n) — uses a Chebyshev filter of the order n.

Arguments

Input arguments

# mode — using the FIR filter

+ line

Details

If the value is set to "fir", then the function decimate uses the function fir1 for designing a low-pass FIR filter with a cutoff frequency 1/r.

# x — input signal

+ vector

Details

The input signal is in the form of a vector.

Data types

Float32, Float64

# r is the decimation coefficient

+ scalar

Details

The decimation coefficient, set as a positive integer. To get the best results when r more 13, divide r use smaller multipliers and call decimate several times.

Data types

Float32, Float64

# n — filtering order

+ scalar

Details

The filtering order is specified as a positive integer. It is not recommended to use the higher filtering order for the IIR filter. 13 due to numerical instability. In such cases, the function outputs a warning.

Data types

Float32, Float64

Output arguments

# y is a signal with a reduced sampling rate

Details

A signal with a reduced sampling rate.

Data types

Float32, Float64

Examples

Signal decimation

Details

Generate a sinusoidal signal with a sampling frequency 4 kHz. Reduce the sampling rate by four times.

import EngeeDSP.Functions: decimate

t = 0:1/4e3:1
x = sin.(2*pi*30*t) + sin.(2*pi*60*t)
y = decimate(x, 4)

Let’s draw graphs of the source and the signal with a reduced sampling rate.

p1 = plot(0:120, x[1:121],
          seriestype = :stem,
          marker = :circle,
          markersize = 3,
          xlabel = "Sample Number",
          ylabel = "Original",
          grid = true,
          legend = false)

p2 = plot(0:30, y[1:31],
          seriestype = :stem,
          marker = :circle,
          markersize = 3,
          xlabel = "Sample Number",
          ylabel = "Decimated",
          grid = true,
          legend = false)

plot(p1, p2, layout = (2, 1))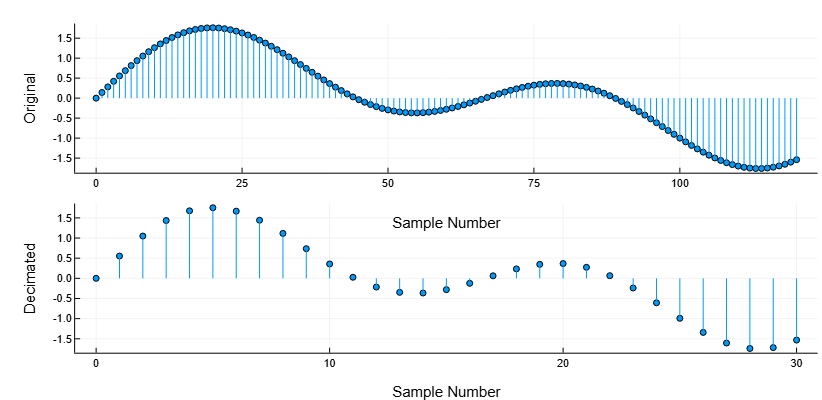

decimate 1

Decimation of the signal using a Chebyshev filter

Details

We will generate a signal from two sinusoids. We will reduce the sampling rate by a factor of 13 using the Chebyshev filter of the fifth order. Let’s plot the source and output signals.

import EngeeDSP.Functions: decimate

r = 13
n = 16:365
lx = length(n)
x = sin.(2*pi*n/153) + cos.(2*pi*n/127)
y = decimate(x, r, 5)

plot(0:lx-1, x,
     seriestype=:scatter,
     marker=:circle,
     label="Original",
     framestyle=:origin,
     grid = true)
plot!(lx-1:-r:0, reverse(y),
      seriestype=:scatter,
      marker=:circle,
      color=:red,
      markersize=4,
      label="Decimated",
      grid = true)

xlabel!("Sample number")
ylabel!("Signal")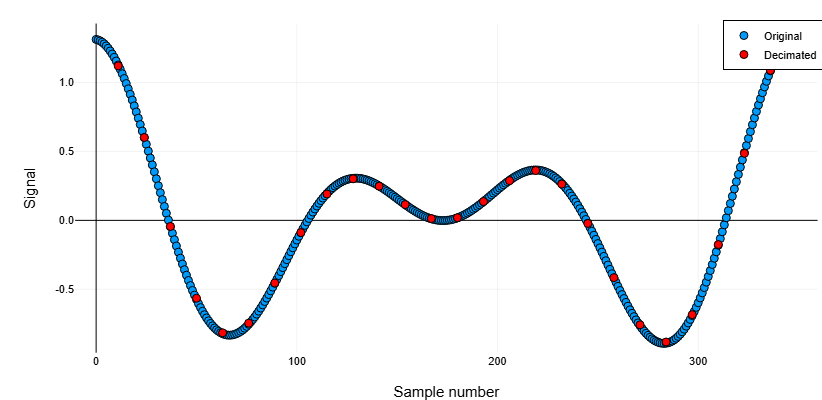

decimate 2

Decimation of the signal using an FIR filter

Details

Generate a sinusoidal signal with a sampling frequency 4 kHz. Reduce the sampling rate by four times.

We will generate a signal from two sinusoids. Reduce the sampling rate by a factor of 13 using an FIR filter. Let’s plot the source and output signals.

import EngeeDSP.Functions: decimate

r = 13
n = 16:365
lx = length(n)
x = sin.(2*pi*n/153) + cos.(2*pi*n/127)
y = decimate(x, r, 82, "fir")

plot(0:lx-1, x,
     seriestype=:scatter,
     marker=:circle,
     label="Original",
     framestyle=:origin,
     grid=true)

plot!(0:r:lx-1, y,
      seriestype=:scatter,
      marker=:circle,
      color=:red,
      markersize=4,
      label="Decimated",
      grid=true)

xlabel!("Sample number")
ylabel!("Signal")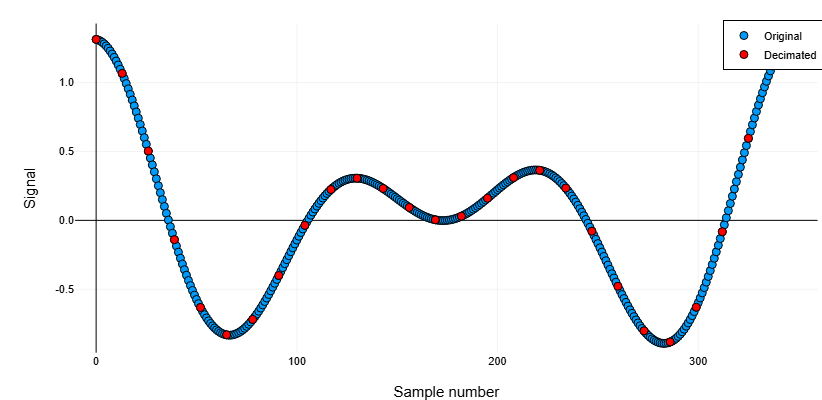

decimate 3

Algorithms

Decimation reduces the initial sampling rate of the sequence to a lower one. This is the opposite of interpolation. Function decimate applies low-pass filtering to the input signal to protect against spectrum aliasing and decimates the result. The function uses the decimation algorithms 8.2 and 8.3 from [1].

decimate creates a low-pass filter. By default, the Chebyshev I BIH filter is used. This filter has a normalized cutoff frequency equal to 0.8/r, and a bandwidth ripple equal to 0.05 dB. Sometimes the specified filtering order leads to bandwidth distortion due to rounding errors accumulated as a result of the convolutions required to create the transfer function. Function decimate automatically reduces the filtering order when distortion causes the amplitude response at the cutoff frequency to differ from the ripple by more than 10^-6.

When selecting an option "fir" function decimate uses the function fir1 for designing a low-pass FIR filter with a cutoff frequency 1/r.
When using an FIR filter, the function decimate filters the input sequence in only one direction. This saves memory and is useful for working with long sequences. In the case of an IIR filter, the function decimate applies the filter in the forward and reverse directions using filtfilt to eliminate phase distortion. In effect, this process doubles the filtering order. In both cases, the function minimizes transient effects at both ends of the signal by matching endpoint conditions.
And finally, the function decimate resamples the data, selecting all r-e points inside the filtered signal. In the re-sampling sequence (y), y(end) respond x(end) when an IIR filter is used, and y(1) respond x(1) when using the FIR filter.

Literature

Digital Signal Processing Committee of the IEEE® Acoustics, Speech, and Signal Processing Society, eds. Programs for Digital Signal Processing. New York: IEEE Press, 1979.