npwgnthresh
Signal-to-noise ratio (SNR) threshold for signal detection in white Gaussian noise.
| Library |
|
Syntax
Function call
You can call the npwgnthresh function in the following ways:
-
snrthresh = npwgnthresh(pfa)calculates the signal-to-noise ratio (SNR) threshold in dB for detecting a deterministic signal in white Gaussian noise. The detection uses the Neyman-Pearson (NP) decisive rule to achieve a given false alarm probability, argument pfa. This function uses a quadratic detector. -
snrthresh = npwgnthresh(pfa,numpulses)sets the numpulses argument as the number of pulses used in pulse integration. -
snrrthresh = npwgnthresh(pfa,numpulses,dettype)sets the data type as the detection type. For non-coherent detection, a rectangular detector is used. -
snrthresh = npwgnthresh(pfa,numpulses,dettype,outscale)specifies the scale of the output.
Arguments
Input
pfa -.
false alarm probability
scalar in the range (0, 1)
Details
Probability of false alarm given as a scalar in the range (0, 1).
Data types: Float64
numpulses
number of pulses
1 (by default) | positive integer
Details
The number of pulses used in the integration, set as a positive integer.
Data types: Float64
dettype -
pulse integration type
noncoherent (by default) | coherent | real
Details
Specifies the type of impulse integration used in the NP decision rule.
Defined as coherent, noncoherent or real.
-
`coherent' uses information about the magnitude and phase of complex samples.
-
`noncoherent' uses quadratic values.
-
realuses real samples.
Data types: char, string
outscale -
output scale
db (by default) | linear
Details
Scale of the output value specified as db or linear.
If the outscale argument is set to linear, the returned threshold is an amplitude.
Data types: char, string
Output
snrthresh -
detection threshold
scalar
Details
Detection threshold specified as a scalar.
The detection threshold is expressed in signal-to-noise ratio (SNR) in dB or in linear units if the outscale argument is set to linear.
The relationship between the linear threshold ( ) and the threshold in dB ( ) is expressed as:
Examples
Linear detection threshold depending on the number of pulses
Details
Graph the linear detection threshold as a function of the number of pulses for real and complex data. In each case, the threshold is set with a false alarm probability (Pfa) of 0.001.
Calculate the detection threshold for 1-10 pulses of real and complex noise.
Npulses = 10
Pfa = 1e-3
snrreal = npwgnthresh.(Pfa, 1:Npulses, "real", "linear")
snrcoh = npwgnthresh.(Pfa, 1:Npulses, "coherent", "linear")
plot([snrreal snrcoh], label = ["Real data with integration" "Complex data with coherent integration"], xlabel = "Number of Pulses", ylabel = "Detection Threshold", title = "Linear Detection Threshold for P_FA = $Pfa", marker = :circle, legendposition = :bottomright)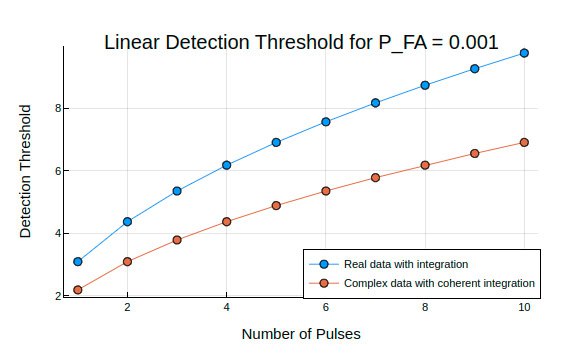
Additional Info
Signal to noise ratio (SNR) threshold when a signal is detected
Details
The output of the npwgnthresh function determines the detection threshold required to achieve a certain false alarm probability (pfa).
The threshold is increased if pulse integration is used in the receiver. This threshold is not the SNR of a single signal that is used as the input of the function rocsnr or the output of the functions rocpfa, albersheim and shnidman.
For any fixed probability of false alarm (pfa) value, you can reduce the single-sample signal-to-noise ratio required to achieve a certain probability of detection (pd) if pulse integration is used in the receiver.
Detecting real signal values in white Gaussian noise
Details
This function is designed to detect a non-zero mean value in a sequence of Gaussian random variables. The function assumes that the random variables are independent and identically distributed, with zero mean value.
The linear detection threshold for the NP detector is equal to:
This threshold can also be expressed as a signal-to-noise ratio in dB:
In these equations
-
- is the variance of the white Gaussian noise sequence;
-
- the number of signals;
-
- the inverse function of the additional error;
-
- false alarm probability.
If the false alarm probability (pfa) is greater than or equal to 1/2, the formula for the detection threshold as a signal-to-noise ratio is invalid because is less than or equal to zero for values of its argument greater than or equal to one. In this case, use the linear output of the function called by the outscale argument with the linear value.
|
Detection of complex signal values in white Gaussian noise (coherent samples)
Details
The following assumptions are made for the npwgnthresh function:
-
The variance of a complex Gaussian random variable is equally divided between the real and imaginary parts.
-
The real and imaginary parts are uncorrelated. According to these assumptions, the linear detection threshold for the NP detector is:
and expressed as the signal-to-noise ratio in dB:
If the false alarm probability (pfa) is greater than or equal to 1/2, the formula for the detection threshold as a signal-to-noise ratio is invalid because is less than or equal to zero for values of its argument greater than or equal to one. In this case, use the linear output of the function called by the outscale argument with the linear value.
|
Detecting incoherent signal values in white Gaussian noise
Details
For incoherent signals in white Gaussian noise, detection of a non-zero mean results in a quadratic law detector. For a detailed derivation, see Richards, M. A. "Fundamentals of Radar Signal Processing.", pp. 324-329.
The linear detection threshold for an incoherent NP detector is:
The threshold value, expressed as signal-to-noise ratio in dB, is:
where is the inverse lower incomplete gamma function, is the false alarm probability, and is the number of pulses.
See also
-
Kay, S. M. "Fundamentals of Statistical Signal Processing: Detection Theory. Upper Saddle River", NJ: Prentice Hall, 1998.
-
Richards, M. A. "Fundamentals of Radar Signal Processing." New York: McGraw-Hill, 2005.