filter
One-dimensional digital filter.
| Library |
|
Syntax
Function call
-
y = filter(b, a, x)— filters the input dataxusing a rational transfer function determined by the coefficients of the numerator and denominatorbanda.For more information about the rational transfer function, see Rational transfer function.
If
a(1)not equal to1, then the functionfilternormalizes the filter coefficients bya(1). Therefore,a(1)must be non-zero.-
If
x— vector, thenfilterreturns filtered data as a vector of the same size asx. -
If
x— the matrix, thenfilteroperates on the first dimension and returns filtered data for each column. -
If
x— a multidimensional array, thenfilteracts on the first dimension of the array, the size of which is not equal to1.
-
Arguments
Input arguments
# b — coefficients of the numerator of the transfer function
+
scalar| vector |the matrix
Details
The coefficients of the numerator of the transfer function, specified as a scalar, vector, or matrix.
For more information about the rational transfer function, see Rational transfer function.
| Data types |
|
| Support for complex numbers |
Yes |
# a — coefficients of the denominator of the transfer function
+
scalar| vector |the matrix
Details
The coefficients of the denominator of the transfer function, specified as a scalar, vector, or matrix.
For more information about the rational transfer function, see Rational transfer function.
| Data types |
|
| Support for complex numbers |
Yes |
# x — input data
+
vector | the matrix | N-dimensional array
Details
Input data specified as a vector, matrix, or N-dimensional array.
| Data types |
|
| Support for complex numbers |
Yes |
# zi — initial conditions for filter delays
+
[] (by default) | vector | the matrix | N-dimensional array
Details
Initial conditions for filter delays, specified as a vector, matrix, or N-dimensional array:
-
If
ziis a vector, then its length should be equal tomax(length(a),length(b))-1. -
If
ziis a matrix or an N-dimensional array, then the size of the initial dimension should bemax(length(a),length(b))-1. The size of each remaining dimension must match the size of the corresponding dimension fromx. For example, consider the possibility of usingfilterin the second dimension (dim = 2) arrayxThe dimension is 3 by 4 by 5. The arrayzimust have a size of[max(length(a),length(b))-1]by 3 by 5.
The default value specified as [] initializes all filter delays to zero.
| Data types |
|
| Support for complex numbers |
Yes |
# dim — measurement for performing filtering
+
scalar
Details
The measurement for performing filtering, set as a positive integer scalar. If no dimension is specified, the first dimension of the array, whose size is not equal, will be used by default. 1.
Consider a two-dimensional input array x.
If dim more than ndims(x), then filter considers x as if it has extra dimensions up to dim with dimensions 1. For example, if x — a 2 by 3 matrix, a dim = 3 Then filter works in the third dimension x as if it has a size of 2 by 3 by 1.
| Data types |
|
Output arguments
# zf — end conditions for filter delays
+
vector | the matrix | N-dimensional array
Details
The final conditions for filter delays, returned as a vector, matrix, or N-dimensional array.
-
If
x— vector, thenzf— length column vectormax(length(a),length(b))-1. -
If
xis a matrix or an N-dimensional array, thenzf— an array of column vectors of this lengthmax(length(a),length(b))-1what is the number of columns inzfequivalent to the number of columns inx. For example, consider the possibility of usingfilterin the second dimension (dim = 2) arrayxThe size is 3 by 4 by 5. The arrayzfwill have a size of[max(length(a),length(b))-1]by 3 by 5.
| Data types |
|
Examples
Moving Average Filter
Details
The moving average filter is a common method of smoothing noisy data. In this example, the filter function is used to calculate the averages of the data vector.
Creating a vector string of the size 1 on 100 sinusoidal data distorted by random noise.
import EngeeDSP.Functions: filter
using Random
Random.seed!(0)
t = range(-pi, pi, length=100)
x = sin.(t) + 0.25 * randn(length(t))The moving average filter moves the window length windowSize along the data, calculating the average value of the data contained in each window. The following difference equation defines a moving average filter for the vector :
For a window the size of 5 let’s calculate the coefficients of the numerator and denominator for a rational transfer function.
windowSize = 5
b = (1/windowSize) * ones(windowSize)
a = [1.0]Let’s find the moving average of the data and compare it with the original data.
y = filter(b, a, x)
plot(t, x,
label="Input Data",
linewidth=1.5,
grid=true)
plot!(t, y,
label="Filtered Data",
linewidth=2,
color=:red)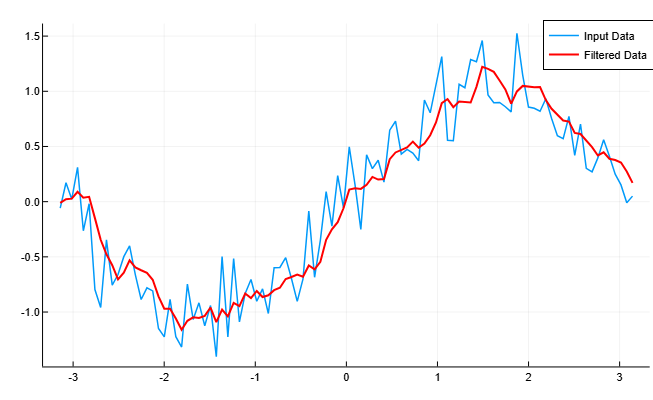
Additional Info
Rational transfer function
Details
Description of the inputs and outputs of the function filter for a vector in the domain, the Z-transform is a rational transfer function. The rational transfer function has the form:
The rational transfer function is applicable to both filters with finite impulse response (FIR) and filters with infinite impulse response (BIH) [1]. Here — Z-conversion of the input signal x, — Z-conversion of the output signal , — the order of the feedback filter, and — the order of the feed-forward filter. In connection with normalization, let’s assume that .
For a discrete signal with the elements can express a rational transfer function in the form of a difference equation:
In addition, it is possible to represent a rational transfer function using its transposed implementation in direct form II, as shown in the diagram of a digital IIR filter. On the diagram . If the orders of the feedback and forward filters are not equal , then the higher-order terms can be considered equal 0. For example, for a filter with a = [1, 2] and b = [2, 3, 2, 4] Can I accept a = [1, 2, 0, 0].
Filter Execution filter at the point of reference It is determined by the difference equations for the time domain:
The default function is filter initializes the filter delays to zero, . With this initialization, it is assumed that both the past input data and the output data are zero. To include non-zero past inputs in the current data, specify the initial conditions for the current data as filter delays. The filter delays can be considered as the end conditions that result from applying the same transfer function to the previous inputs (and the previous outputs). You can specify a fourth input argument. zi when using filter to set filter delays, zi(k). You can also specify a second output argument. zf when using filter to access the end conditions, zf(k).


