dpss
Discrete elongated spheroidal sequences (Slepyan sequences).
| Library |
|
Syntax
Function call
-
dpsSeq, lambda = dpss(seqLength, timeHalfBW)— returns the first oneround(2*timeHalfBW)a discrete elongated spheroidal sequence (DPSS) of lengthseqLengthand energy concentration ratioslambdain the frequency domain for column vectorsdpsSeq. These ratios represent the ratio of the amount of energy in the bandwidth. to the total energy in the range , where — sampling rate.
-
dpsSeq, lambda = dpss(seqLength, timeHalfBW, numSeq)— returns the first onesnumSeqDPSS sequences with the product of time and half the bandwidthtimeHalfBW. The function returns sequences in the order of their energy concentration ratios.
-
dpsSeq, lambda = dpss(_, dpssLength)— interpolates DPSS sequences of lengthdpssLength.
Arguments
Input arguments
# seqLength is the length of the sequence
+
positive integer
Details
The length of the sequence, specified as a positive integer.
| Data types |
|
# numSeq — number of sequences
+
positive integer | two-element vector
Details
The number of sequences to return, specified as a positive integer or a two-element vector. If you specify numSeq as a two-element vector, Slepyan’s output sequences will range from numSeq(1) before numSeq(2).
| Data types |
|
# dpssLength is the length of the sequence
+
positive integer
Details
The length of DPSS sequences, set as a positive integer.
| Data types |
|
Output arguments
# dpsSeq — Slepyan sequences (DPSS)
+
the matrix
Details
Slepyan sequences returned as a matrix with the number of rows equal to seqLength, and columns equal to round(2*timeHalfBW).
# lambda — energy concentration ratios in the frequency domain
+
column vector
Details
The energy concentration ratio in the frequency domain, returned as a column vector with a length equal to the number of Slepian sequences.
Examples
Generating a set of Slepyan sequences
Details
Let’s construct the first four discrete elongated spheroidal sequences of length 512. Let’s set the product of time by half the bandwidth equal to 2. Let’s plot the sequence graphs and display the concentration ratios.
import EngeeDSP.Functions: dpss
seq_length = 512
time_halfbandwidth = 2
num_seq = 4
dps_seq, lambda = dpss(seq_length, time_halfbandwidth, num_seq)
plot(dps_seq,
title="Slepian Sequences, N = 512, NW = 2",
xlims=(0, 512),
ylims=(-0.15, 0.15),
label=["1st" "2nd" "3rd" "4th"])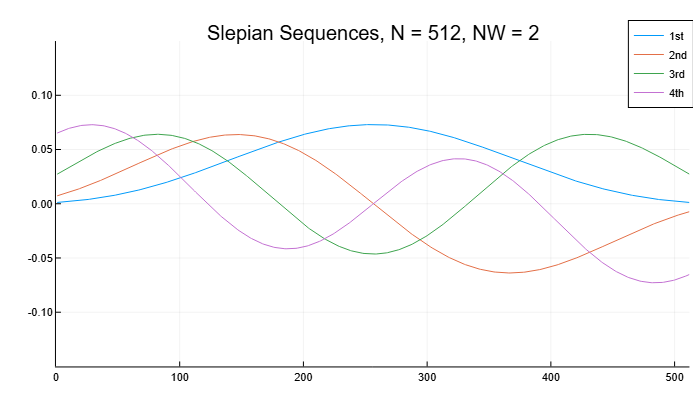
Additional Info
Discrete elongated spheroidal sequences
Details
Discrete elongated spheroidal sequences, or Slepyan sequences, are derived from the following problem of time-frequency concentration. For all sequences with finite energy the index is limited to some set , for which the sequence maximizes this ratio:
where — sampling rate, and . Accordingly, this ratio determines which sequence with a limited index has the largest share of energy in the band. . For sequences with a limited index, the relation must satisfy the inequality . The sequence maximizing the ratio is the first discrete elongated spheroidal sequence, or Slepyan sequence. The second Slepyan sequence maximizes the ratio and is orthogonal to the first Slepyan sequence. Slepyan’s third sequence maximizes the ratio of integrals and is orthogonal to both the first and second Slepyan sequences. Continuing in this way, Slepyan sequences form an orthogonal set of sequences with a limited band.
The product of time by half the bandwidth
Details
The product of time by half the bandwidth is , where — the length of the sequence, and is the effective bandwidth of the sequence. When constructing Slepyan sequences, you select the desired sequence length and bandwidth. . Both the length of the sequence and the bandwidth affect the number of Blind sequences with concentration coefficients close to unity. As a rule, there are Slepyan sequences with energy concentration coefficients approximately equal to unity. Beyond After the Blind sequences, the concentration coefficients begin to tend to zero. Common variants of the product of time by half the bandwidth: 2.5, 3, 3.5 and 4.
You can specify the bandwidth of the Slepian sequences in Hz by defining the product of time and half the bandwidth as , where — sampling rate.