Python neural networks and their integration with Engee models
In this demo, we will look at an example of neural network training using the sklearn package.
To work with neural networks using Python, Engee uses the PyCall package and Python invocation commands in Engee.
First, install the sklearn and PyPlot libraries in Engee.
# Pkg.add("ScikitLearn")
Pkg.add("PyPlot")
using PyPlot
# Импорт необходимых модулей из Python
@pyimport sklearn.neural_network as nn
@pyimport sklearn.tree as tree
@pyimport numpy as np
Generating training data from a model in Engee
This model generates a vector of two sine wave values, which represent a single signal for the classifier. Based on the determination of the amplitude oscillation of the output signal, class labels are set. The figure below shows the upper level of the model.
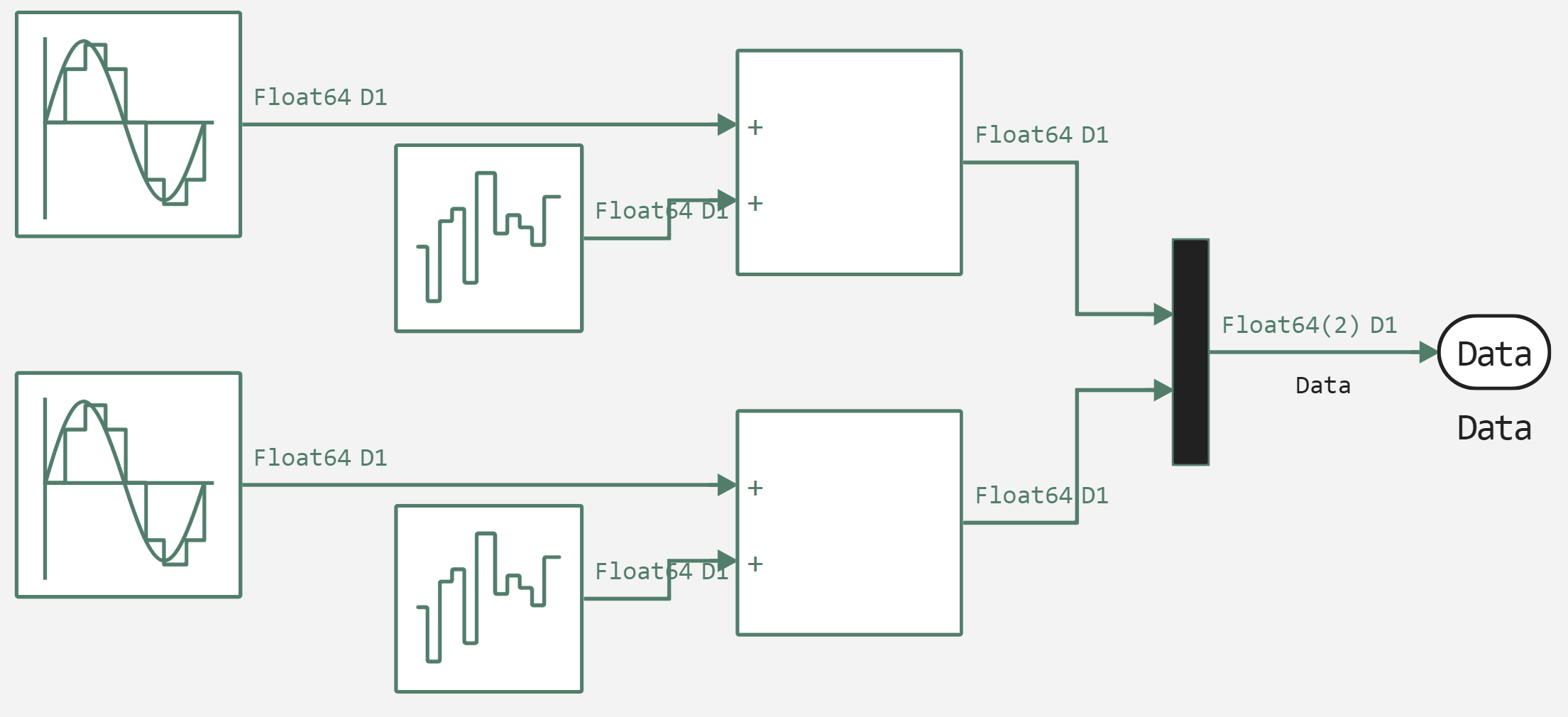
In the figure below, you can see the data generation process.
The following shows the formation of a class label across three ranges:
- less than -0.7;
- more than -0.7 and less than 0.7;
- more than 0.7.
Let's move on to data generation, for which we will connect the auxiliary function of launching the model, launch the model and look at what data has been uploaded to simout.
function run_model(name_model)
Path = (@__DIR__) * "/" * name_model * ".engee"
if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
model = engee.open( name_model ) # Открыть модель
model_output = engee.run( model, verbose=true ); # Запустить модель
else
model = engee.load( Path, force=true ) # Загрузить модель
model_output = engee.run( model, verbose=true ); # Запустить модель
engee.close( name_model, force=true ); # Закрыть модель
end
return model_output
end
run_model("PyDataGen")
sleep(1)
collect(simout)
Next, we will download the data from simout and convert it to the numpy format for further feeding it to Python neural networks.
target = simout["PyDataGen/target"];
target = collect(target);
target = np.array(target.value);
Data = simout["PyDataGen/Data"];
Data = collect(Data);
Data = np.array(Data.value);
Multi-layer perceptron
The first classifier network, which we will consider in this demonstration, is a multilayer perceptron network for predicting belonging to a data group by oscillation amplitude.
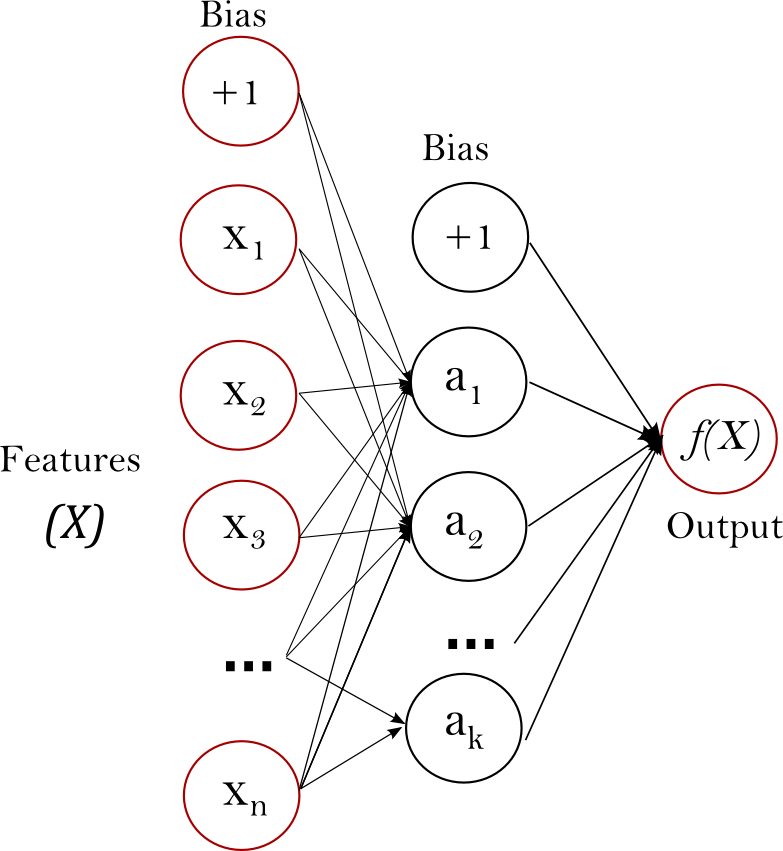
A multilayer perceptron (MLP) is a feed–forward artificial neural network model that maps sets of input data to a set of corresponding output data. MLP consists of several levels, each of which is fully connected to the next one. The nodes of the layers are neurons with nonlinear activation functions, except for the nodes of the input layer. There may be one or more non-linear hidden layers between the input and output layers.
The figure below shows an MLP with a single hidden layer with a scalar output.
Let's move on to initializing and training a neural network in Python. There are several parameters available for configuring MLP:
- hidden_layer_sizes – the size of the hidden layer;
- max_iter – the maximum allowed number of training iterations;
- alpha – the learning step;
- solver – a solver that defines an algorithm for optimizing weights across nodes;
- verbose – indicates whether to output additional information;
- random_state – setting for managing random values;
- learning_rate_init – learning rate.
clf = nn.MLPClassifier(hidden_layer_sizes=(100,), max_iter=10, alpha=1e-4, solver="sgd", verbose=1, random_state=1, learning_rate_init=.1)
clf[:fit](Data, target)
As we can see from the warning, the maximum number of iterations was reached, but the optimization did not converge. Therefore, it is necessary to increase the number of iterations. Let's repeat the initialization and training of the neural network in Python with new network parameters.
clf = nn.MLPClassifier(hidden_layer_sizes=(100,), max_iter=140, alpha=1e-4, solver="sgd", verbose=1, random_state=1, learning_rate_init=.1)
clf[:fit](Data, target)
Now let's evaluate the quality of the model. As we can see, the neural network has a high guessing accuracy.
accuracy = clf[:score](Data, target)
println("Точность: $accuracy")
Decision tree
Let's look at an example of code for training a neural network with a decision tree structure. It is a nonparametric teaching method with a teacher used for classification and regression.
As part of this method, it is required to create a model that predicts the value of the target variable by studying simple decision-making rules derived from data features.
The tree can be considered as a piecewise constant approximation. Let's start by declaring and training the decision tree.
dt_clf = tree.DecisionTreeClassifier()
dt_clf.fit(Data, target)
Let's build a graph of the decision tree and increase the pixel size and density to make the graph more visual.
plt.figure(figsize=(13, 4), dpi=200)
tree.plot_tree(dt_clf, filled=true)
Let's create a new graph for the output of the neural network result.
plt.figure(figsize=(18, 6), dpi=80) # увеличим размер и плотность пикселей
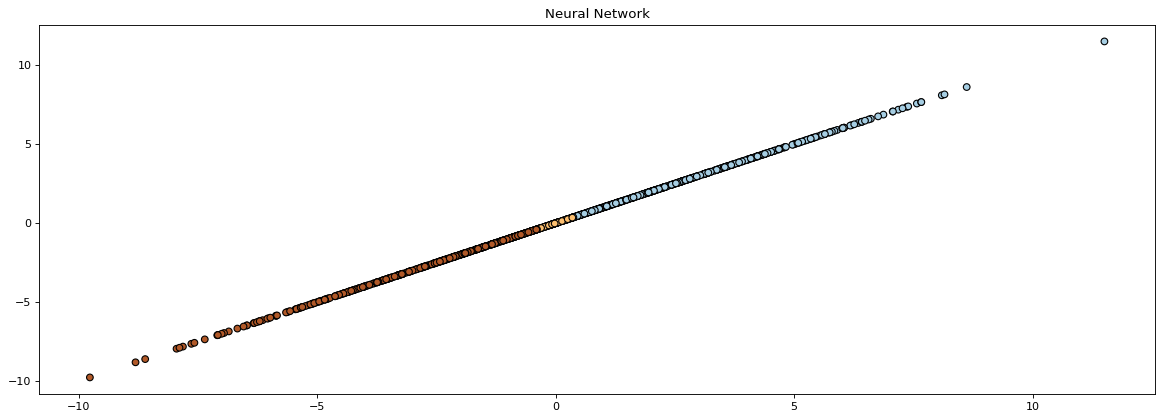
plt.scatter(Data[:, 1], Data[:, 2], c=target, cmap=plt.cm.Paired, edgecolors="k")
plt.title("Neural Network")
As we can see from the resulting graph, all the values we generated were divided into three separate groups based on the sum of the input data.
Conclusion
Using concrete examples, we have shown the options for integrating neural networks into Engee, as well as the possibilities of combining model-oriented design and Python functionality.