smoothdata
Сглаживание зашумленных данных.
| Библиотека |
|
Синтаксис
Вызов функции
-
B = smoothdata(A)— сглаживает элементыAс помощью скользящего среднего. Функцияsmoothdataопределяет размер скользящего окна на основе элементовA. Окно перемещается по длине вектора, вычисляя среднее значение по элементам каждого окна. ЕслиA— матрица, то функцияsmoothdataвычисляет скользящее среднее по каждому столбцуA.
-
B = smoothdata(___, Name,Value)— использует дополнительные параметры для сглаживания, заданные одним или несколькими аргументами типаName,Value.
Аргументы
Входные аргументы
#
A —
входные данные
вектор | матрица
Details
Входные данные, заданные как вектор или матрица.
| Типы данных |
|
| Поддержка комплексных чисел |
Да |
#
dim —
измерение, по которому выполняется операция
скаляр
Details
Измерение, по которому выполняется операция, заданное как положительный целочисленный скаляр. Если измерение не указано, то по умолчанию используется первое измерение массива, размер которого не равен 1.
Рассмотрим входную матрицу A размером на :
#
method —
метод сглаживания
"movmean" (по умолчанию) | "movmedian" | "gaussian" | "lowess" | "loess" | "rlowess" | "rloess" | "sgolay"
Details
Метод сглаживания, заданный одним из следующих значений:
-
"movmean"— среднее по каждому окнуA. Этот метод полезен для уменьшения периодических трендов в данных. -
"movmedian"— медиана по каждому окнуA. Этот метод полезен для уменьшения периодических трендов в данных при наличии выбросов. -
"gaussian"— гауссовское средневзвешенное по каждому окнуA. -
"lowess"— линейная регрессия по каждому окнуA. Этот метод может быть вычислительно затратным, но приводит к меньшему количеству разрывов. -
"loess"— квадратичная регрессия по каждому окнуA. Этот метод более вычислительно затратен, чем"lowess". -
"rlowess"— устойчивая линейная регрессия по каждому окнуA. Этот метод является более вычислительно затратной версией метода"lowess", но более устойчив к выбросам. -
"rloess"— робастная квадратичная регрессия для каждого окнаA. Этот метод является более вычислительно затратной версией метода"lowess", но более устойчив к выбросам. -
"sgolay"— фильтр Савицкого — Голея, который сглаживает данные в соответствии с квадратичным полиномом, подобранным для каждого окнаA. Этот метод может быть эффективнее других методов, когда данные быстро меняются.
#
window —
размер окна
скаляр | двухэлементный вектор
Details
Размер окна, заданный как положительный целочисленный скаляр или двухэлементный вектор неотрицательных целых чисел. Функция smoothdata определяет окно относительно точек выборки.
-
Если
window— это положительный целочисленный скаляр, то окно имеет длинуwindowи центрируется относительно текущего элемента. -
Если
window— это двухэлементный вектор неотрицательных целых чисел[b f], то окно содержит текущий элемент,bпредшествующих элементов иfпоследующих элементов.
Дополнительную информацию о положении окна см. в разделе Размер скользящего окна.
#
nanflag —
условие отсутствия значения
"omitmissing" (по умолчанию) | "omitnan" | "includemissing" | "includenan"
Details
Условие отсутствия значения, заданное одним из следующих значений:
-
"omitmissing"или"omitnan"— игнорировать значенияNaNвAпри сглаживании. Если все элементы в окне —NaN, то соответствующие элементы вBтакжеNaN. Значения"omitmissing"и"omitnan"ведут себя одинаково. -
"includemissing"или"includenan"— включить значенияNaNвAпри сглаживании. Если какой-либо элемент в окне —NaN, то соответствующие элементы вBтакжеNaN. Значения"includemissing"и"includenan"ведут себя одинаково.
Входные аргументы «имя-значение»
Укажите необязательные пары аргументов в формате Name, Value, где Name — имя аргумента, а Value — соответствующее значение. Аргументы типа «имя-значение» должны располагаться после других аргументов, но порядок пар не имеет значения.
Используйте запятые для разделения имени и значения, а Name заключите в кавычки.
Пример: B = smoothdata([4.2, 3.8, 4.3, 5], "SmoothingFactor", 0.5).
#
SmoothingFactor —
коэффициент размера окна
скаляр
Details
Коэффициент размера окна, заданный как скаляр в диапазоне от 0 до 1. Как правило, значение SmoothingFactor регулирует уровень сглаживания, масштабируя размер окна, который функция smoothdata определяет на основе значений в A. Значения, близкие к 0, приводят к уменьшению размера окна, что приводит к меньшему сглаживанию. Значения, близкие к 1, приводят к увеличению размера окна, что приводит к большему сглаживанию. В некоторых случаях, в зависимости от значений, используемых smoothdata для определения размера окна, значение аргумента SmoothingFactor может не оказывать существенного влияния на размер окна.
По умолчанию значение аргумента SmoothingFactor равно 0.25. Указать SmoothingFactor можно только если не указано window.
#
Degree —
степень фильтра Савицкого — Голея
скаляр
Details
Степень фильтра Савицкого — Голея, заданная как неотрицательный целочисленный скаляр. Этот аргумент типа «имя-значение» может быть указан только в том случае, если выбран метод сглаживания "sgolay". Значение аргумента Degree соответствует степени полинома в фильтре Савицкого — Голея, который аппроксимирует данные в каждом окне. По умолчанию оно равно 2.
Значение аргумента Degree должно быть меньше размера окна для равномерных точек выборки. Для неравномерных точек выборки значение должно быть меньше максимального количества точек в любом окне.
Выходные аргументы
#
winsize —
размер окна
скаляр | двухэлементный вектор
Details
Размер окна, возвращаемый в виде положительного целочисленного скаляра или двухэлементного вектора неотрицательных целых чисел.
Примеры
Сглаживание данных с помощью скользящего среднего
Details
Создадим вектор, содержащий зашумленные данные, и сгладим данные с помощью скользящего среднего. Построим график исходных и сглаженных данных.
import EngeeDSP.Functions: smoothdata
using Plots, Random
Random.seed!(0)
x = 1:100
A = cos.(2π * 0.05 * x .+ 2π * rand()) .+ 0.5 * randn(100)
B = smoothdata(A)
plot(x, A, label="Input Data")
plot!(x, B, label="Smoothed Data")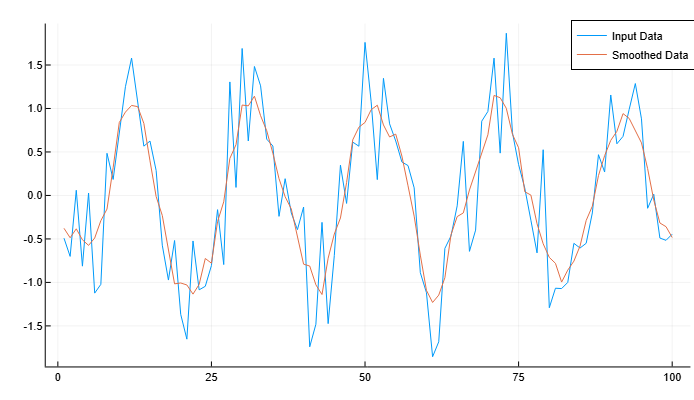
Матрица зашумленных данных
Details
Создадим матрицу, строки которой представляют три зашумленных сигнала. Сгладим эти три сигнала с помощью скользящего среднего и построим график сглаженных данных.
import EngeeDSP.Functions: smoothdata
using Plots, Random
Random.seed!(0)
x = 1:100
s1 = cos.(2π * 0.03 * x .+ 2π * rand(rng)) .+ 0.5 * randn(rng, 100)
s2 = cos.(2π * 0.04 * x .+ 2π * rand(rng)) .+ 0.4 * randn(rng, 100) .+ 5
s3 = cos.(2π * 0.05 * x .+ 2π * rand(rng)) .+ 0.3 * randn(rng, 100) .- 5
A = [s1'; s2'; s3']
B = smoothdata(A, 2)[1]
plot(x, B[1, :], label="s1")
plot!(x, B[2, :], label="s2")
plot!(x, B[3, :], label="s3")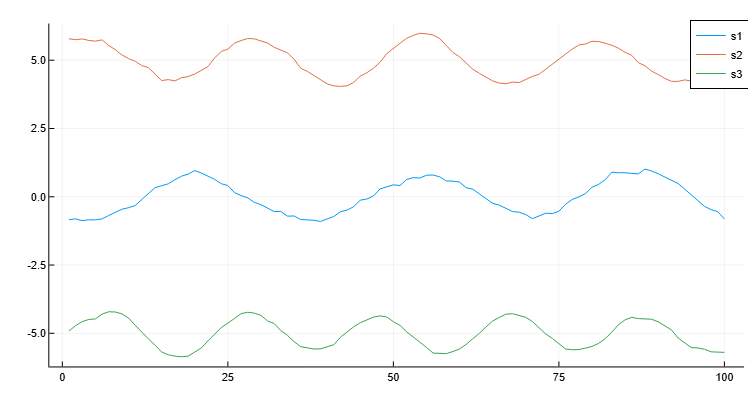
Гауссов фильтр
Details
Сгладим вектор зашумленных данных с помощью фильтра скользящего среднего, взвешенного по Гауссу. Отобразим размер окна, используемого фильтром.
import EngeeDSP.Functions: smoothdata
using Plots, Random
Random.seed!(0)
x = 1:100
A = cos.(2π * 0.05 * x .+ 2π * rand(rng)) .+ 0.5 * randn(rng, 100)
B, winsize = smoothdata(A, "gaussian")
winsize4.0Сгладим исходные данные с помощью окна большего размера, содержащего 20 элементов. Построим график сглаженных данных для окон обоих размеров.
C = smoothdata(A, "gaussian", 20)[1]
plot(x, B, label="Small Window", linewidth=2)
plot!(x, C, label="Large Window", linewidth=2)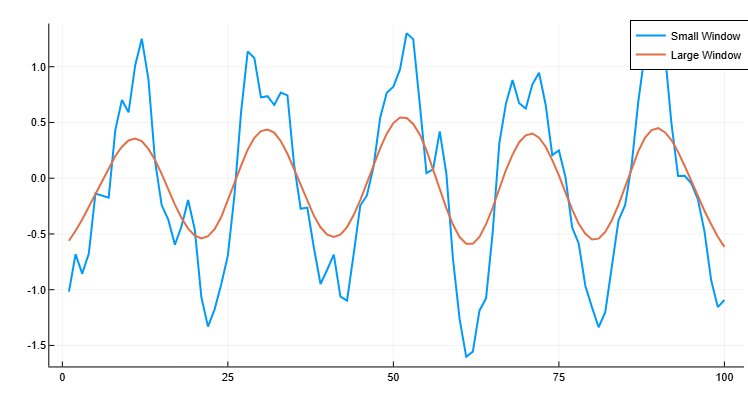
Сглаживание данных с отсутствующими значениями
Details
Создадим зашумленный вектор, содержащий значения NaN, и сгладим данные, игнорируя значения NaN.
import EngeeDSP.Functions: smoothdata
A = [NaN randn(1,48) NaN randn(1,49) NaN]
B, w = smoothdata(A)([NaN 0.5580616078303169 … 1.0570367844487276 2.3203045641188864], 2.0)Сгладим данные, включая значения NaN. Среднее значение в окне, содержащем хотя бы одно значение NaN, равно NaN.
C, w = smoothdata(A, "includenan")([NaN NaN … 1.0570367844487276 NaN], 2.0)Построим графики сглаженных векторов B и C.
plot(1:100, B', shape=:circle, label="Ignore Missing")
plot!(1:100, C', shape=:xcross, label="Include Missing")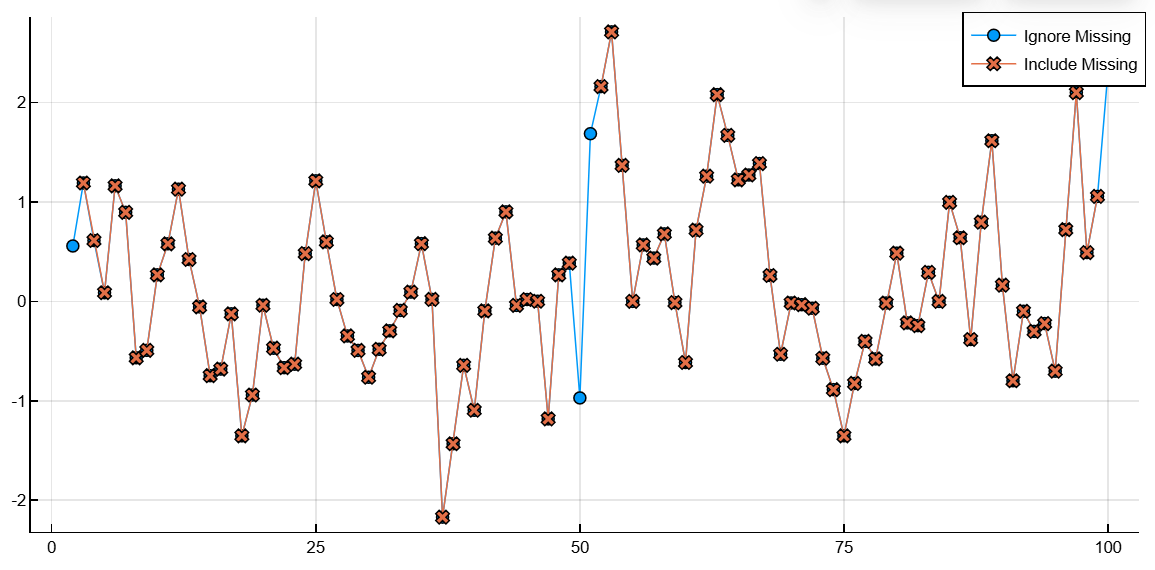
Дополнительно
Размер скользящего окна
Details
В этой таблице показано положение окна по вектору равномерно распределенных точек выборки по умолчанию [1 2 3 4 5 6 7].
| Описание | Размер окна и положение | Точки выборки в окне | Схема |
|---|---|---|---|
Для скалярного размера окна передний край окна включается, а задний край окна исключается. |
|
|
|
|
|
||
Для определения размера векторного окна учитываются передний и задний край. |
|
|
|
Для точек выборки, расположенных вблизи конечных точек входных данных, эти методы сглаживания скользящей статистики усекают окно так, чтобы оно начиналось с первой точки выборки или заканчивалось с последней:
|
|
|
|
Для точек выборки, расположенных вблизи конечных точек входных данных, эти методы локального регрессионного сглаживания сдвигают окно так, чтобы оно включало первую или последнюю точку выборки:
|
|
|






