meanfreq

Страница в процессе разработки.

Средняя частота.

Библиотека

EngeeDSP

Синтаксис

Вызов функции

freq, power = meanfreq(x) — оценивает среднюю нормированную частоту freq сигнала во временной области x. Также возвращает спектральную мощность power в заданной полосе частот. Для вычисления спектральной мощности meanfreq использует функцию periodogram с прямоугольным окном и количеством точек ДПФ, равным длине x.

freq, power = meanfreq(x,Fs) — оценивает среднюю частоту в единицах частоты дискретизации Fs.

freq, power = meanfreq(pxx,f) — возвращает среднюю частоту оценки спектральной плотности мощности pxx. Частоты f соответствуют оценкам в pxx.

freq, power = meanfreq(sxx,f,rbw) — возвращает среднюю частоту оценки спектра мощности sxx с полосой разрешения rbw.

freq, power = meanfreq(___,freqRange) — также использует частотный интервал freqRange, на котором вычисляется средняя частота. Этот синтаксис может включать любую комбинацию входных аргументов из предыдущих синтаксисов, при условии, что второй входной аргумент равен либо Fs либо f. Если второй входной аргумент передан пустым, то meanfreq использует нормализованную частоту. Значение по умолчанию для freqRange — вся полоса пропускания входного сигнала.

meanfreq(___,out=:plot) — строит график спектральной плотности мощности или спектра мощности и аннотирует среднюю частоту.

Аргументы

Входные аргументы

# x — входной сигнал
вектор | матрица

Details

Входной сигнал, заданный как вектор или матрица. Если x — вектор, то meanfreq обрабатывает его как одиночный канал. Если x — матрица, то функция вычисляет среднюю частоту независимо для каждого столбца x.

Типы данных

Float32, Float64

# Fs — частота дискретизации
положительный вещественный скаляр

Details

Частота дискретизации, заданная как положительный вещественный скаляр. Частота дискретизации — это количество отсчетов в единицу времени. Если единицей времени являются секунды, то частота дискретизации указывается в Гц.

Типы данных

Float32, Float64

# pxx — спектральная плотность мощности
вектор | матрица

Details

Спектральная плотность мощности, заданная как вектор или матрица. Если pxx — матрица, то meanfreq вычисляет среднюю частоту независимо для каждого столбца pxx.

Спектральная плотность мощности должна быть выражена в линейных единицах, а не в дБ.

Типы данных

Float32, Float64

# f — частоты
вектор

Details

Частоты, заданные как вектор.

Типы данных

Float32, Float64

# sxx — оценка спектральной мощности
вектор | матрица

Details

Оценка спектральной мощности, заданная как вектор или матрица. Если sxx — матрица, то meanfreq вычисляет среднюю частоту независимо для каждого столбца sxx.

Спектральная плотность мощности должна быть выражена в линейных единицах, а не в дБ.

Типы данных

Float32, Float64

# rbw — разрешающая способность по частоте
положительный скаляр

Details

Разрешающая способность по частоте, заданная как положительный скаляр. Разрешающая способность по частоте определяется как произведение двух величин: частотного разрешения дискретного преобразования Фурье и эквивалентной ширины полосы шума окна, используемого для вычисления спектральной плотности мощности.

Типы данных

Float32, Float64

# freqRange — диапазон частот
двухэлементный вектор

Details

Диапазон частот, заданный как двухэлементный вектор вещественных значений. Если freqRange не указан, то meanfreq использует всю полосу пропускания входного сигнала.

Типы данных

Float32, Float64

Выходные аргументы

# freq — средняя частота
скаляр | вектор

Details

Средняя частота, возвращаемая в виде скаляра или вектора.

Если вы указываете частоту дискретизации, то freq имеет те же единицы измерения, что и Fs.
Если частота дискретизации не указана, то freq имеет единицы измерения рад/отсчет.

# power — спектральная мощность в полосе частот
скаляр | вектор

Details

Спектральная мощность в полосе частот, возвращаемая в виде скаляра или вектора.

Примеры

Средняя частота чирп сигнала

Details

Сгенерируем 1024 отсчета чирп сигнала с частотой дискретизации 1024 кГц. Зададим частоту чирпа так, чтобы она начиналась с 50 кГц и достигала 100 кГц в конце сигнала. Добавим белый гауссовский шум таким образом, чтобы отношение сигнал/шум составляло 40 дБ. Перезапустим генератор случайных чисел для получения воспроизводимых результатов.

import EngeeDSP.Functions: meanfreq, chirp, std
using Random

nSamp = 1024
Fs = 1024e3
SNR = 40
Random.seed!(0)
t = (0:nSamp-1)./ Fs
x = chirp(t, 50e3, nSamp/Fs, 100e3)
x = x.+ randn(nSamp).* std(x)[1]./(10^(SNR/20))

Оценим среднюю частоту чирп сигнала. Построим график спектральной плотности мощности и определим среднюю частоту.

meanfreq(x,Fs,out=:plot)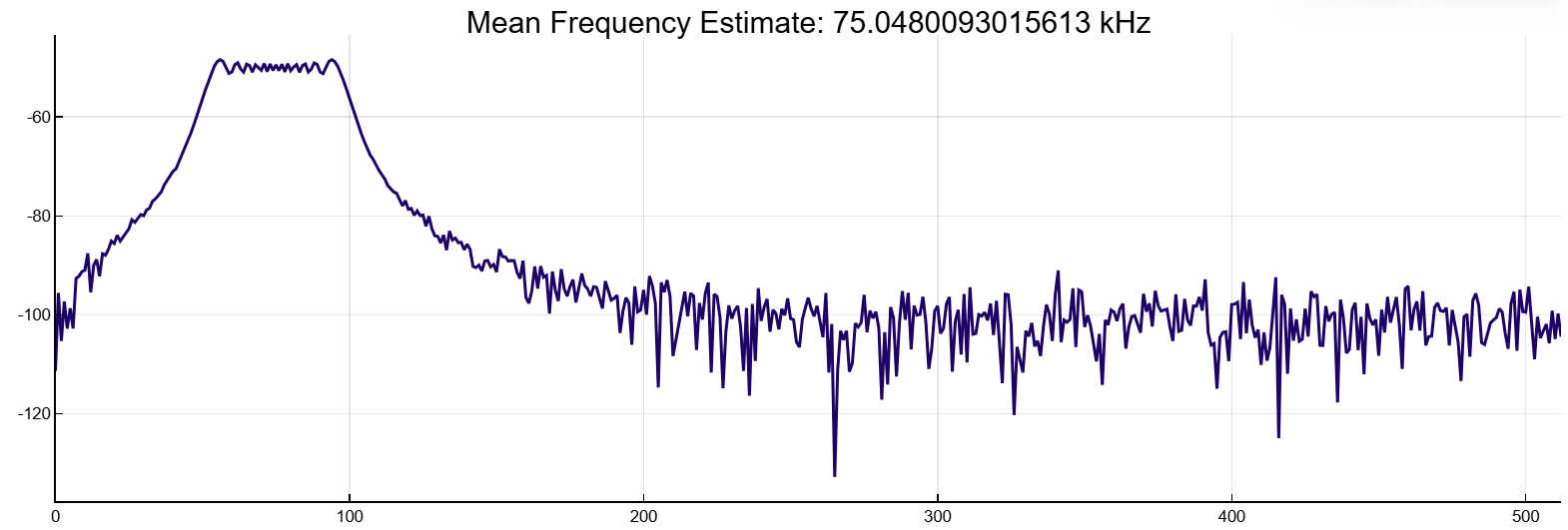

meanfreq 1

Сгенерируем еще один чирп сигнал. Зададим начальную частоту 200 кГц, конечную частоту 300 кГц и амплитуду, вдвое превышающую амплитуду первого сигнала. Добавим белый гауссовский шум.

x2 = 2*chirp(t,200e3,nSamp/Fs,300e3)
x2 = x2.+ randn(nSamp).* std(x2)[1]./(10^(SNR/20))

Объединим чирп сигналы для получения двухканального сигнала. Оценим среднюю частоту каждого канала.

y = meanfreq([x x2],Fs)

([75048.0093015613 250002.6501495102], [0.49966449511918404 2.0006502475894763])

Построим графики спектральной плотности мощности двух каналов.

y = meanfreq([x x2],Fs,out=:plot)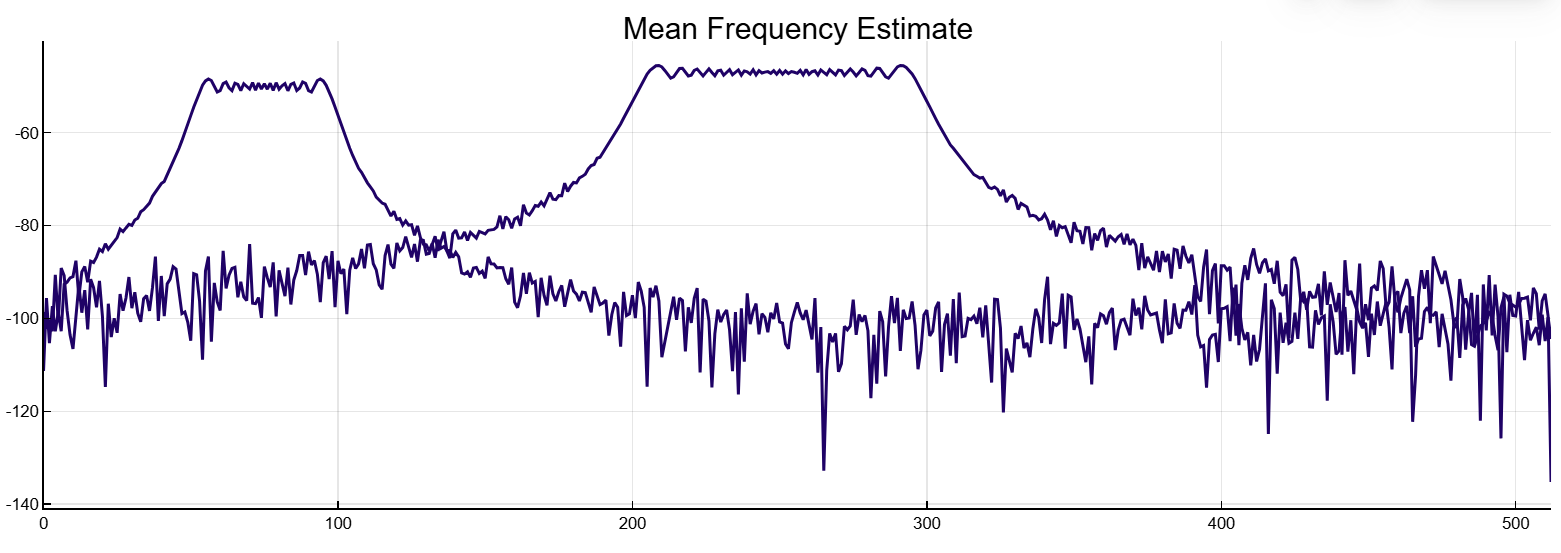

meanfreq 2

Сложим два канала, чтобы сформировать новый сигнал. Построим график спектральной плотности мощности и определим среднюю частоту.

y = meanfreq(x+x2,Fs,out=:plot)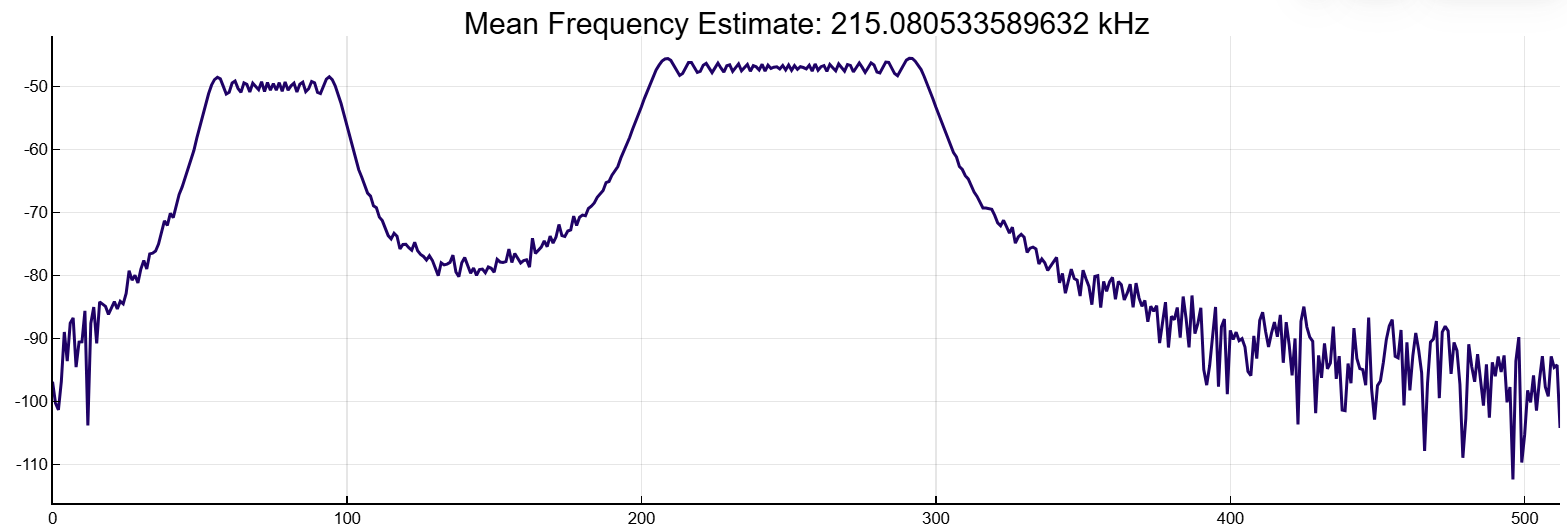

meanfreq 3

Средняя частота синусоиды

Details

Сгенерируем 1024 отсчета синусоидального сигнала с частотой 100.123 кГц, дискретизированный с частотой 1024 кГц. Добавим белый гауссовский шум таким образом, чтобы отношение сигнал/шум составляло 40 дБ. Перезапустим генератор случайных чисел для получения воспроизводимых результатов.

import EngeeDSP.Functions: meanfreq, sin, std
using Random

nSamp = 1024
Fs = 1024e3
SNR = 40
Random.seed!(0)
t = (0:nSamp-1)./ Fs
x = sin.(2pi * t * 100.123e3)
x = x.+ randn(nSamp).* std(x)[1]./(10^(SNR/20))

Оценим среднюю частоту синусоидального сигнала. Построим график спектральной плотности мощности и определим среднюю частоту.

meanfreq(x,Fs,out=:plot)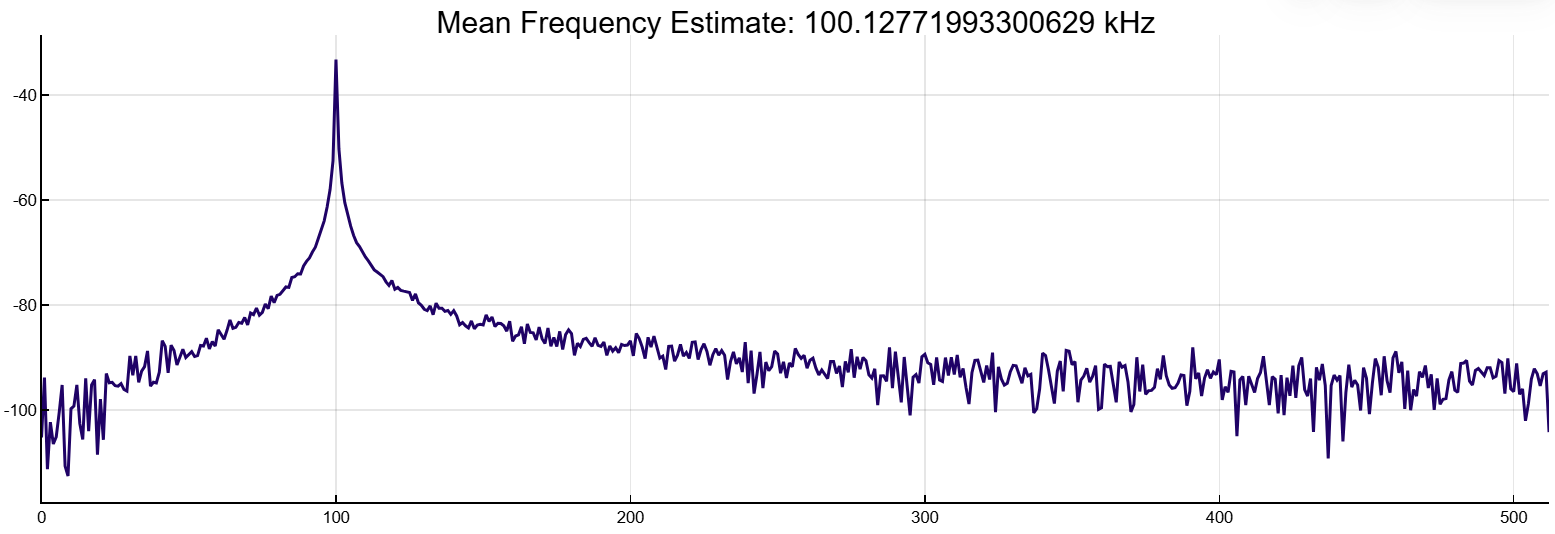

meanfreq 4

Сгенерируем еще один синусоидальный сигнал с частотой 257.321 кГц и амплитудой, в два раза превышающей амплитуду первой синусоиды. Добавим белый шум.

x2 = sin.(2pi * t * 257.321e3)
x2 = x2.+ randn(nSamp).* std(x2)[1]./(10^(SNR/20))

Объединим синусоиды для получения двухканального сигнала. Оценим среднюю частоту каждого канала.

y = meanfreq([x x2],Fs)

([100127.71993300629 257421.94010929883], [0.4996432155771679 0.4994390782715168])

Построим графики спектральной плотности мощности двух каналов.

y = meanfreq([x x2],Fs,out=:plot)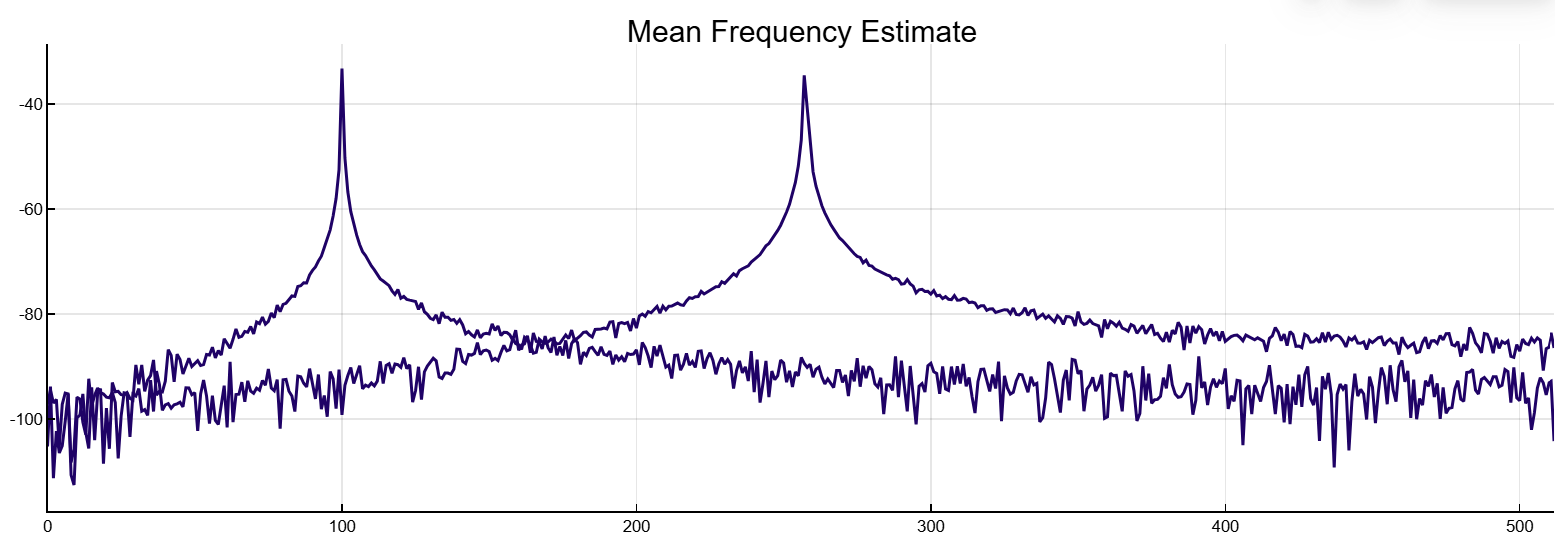

meanfreq 5

y = meanfreq(x+x2,Fs,out=:plot)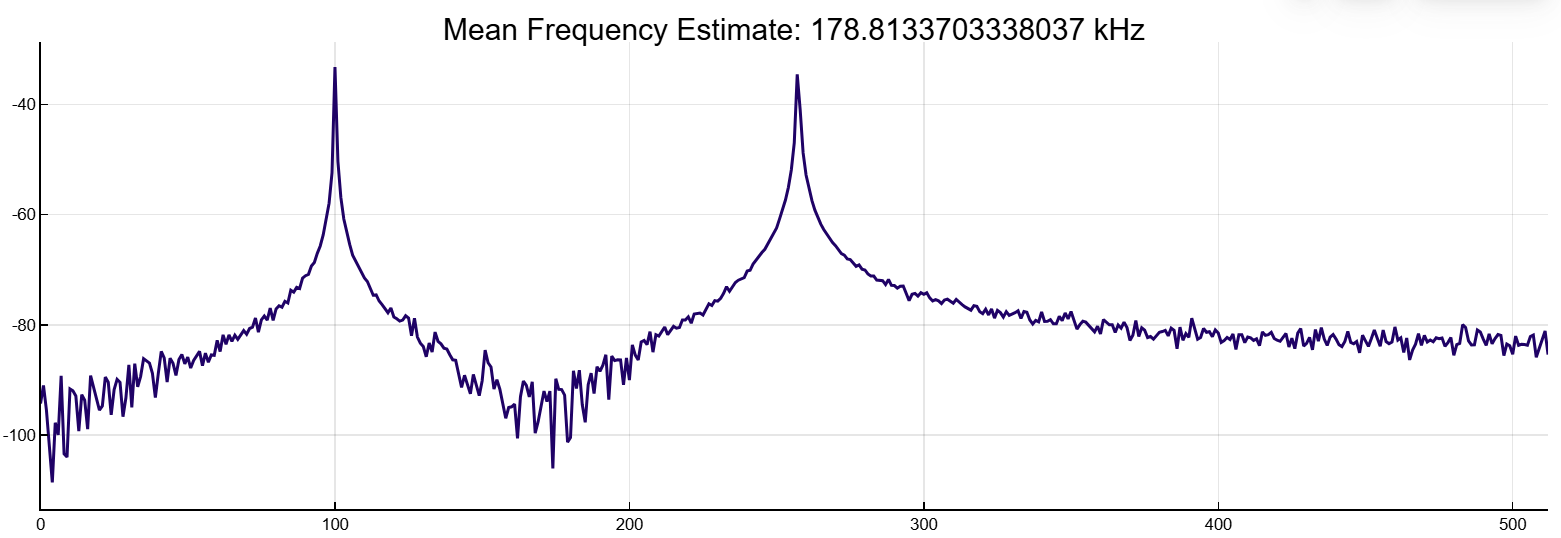

meanfreq 6

Средняя частота сигналов ограниченных по полосе

Details

Создадим сигнал, спектральная плотность мощности которого напоминает частотную характеристику полосового КИХ-фильтра 88-го порядка с нормированными частотами среза.

import EngeeDSP.Functions: fir1, meanfreq, bandpower

d = fir1(88,[0.25 0.45])

meanfreq(d,[],[0.3 0.6]*pi, out=:plot)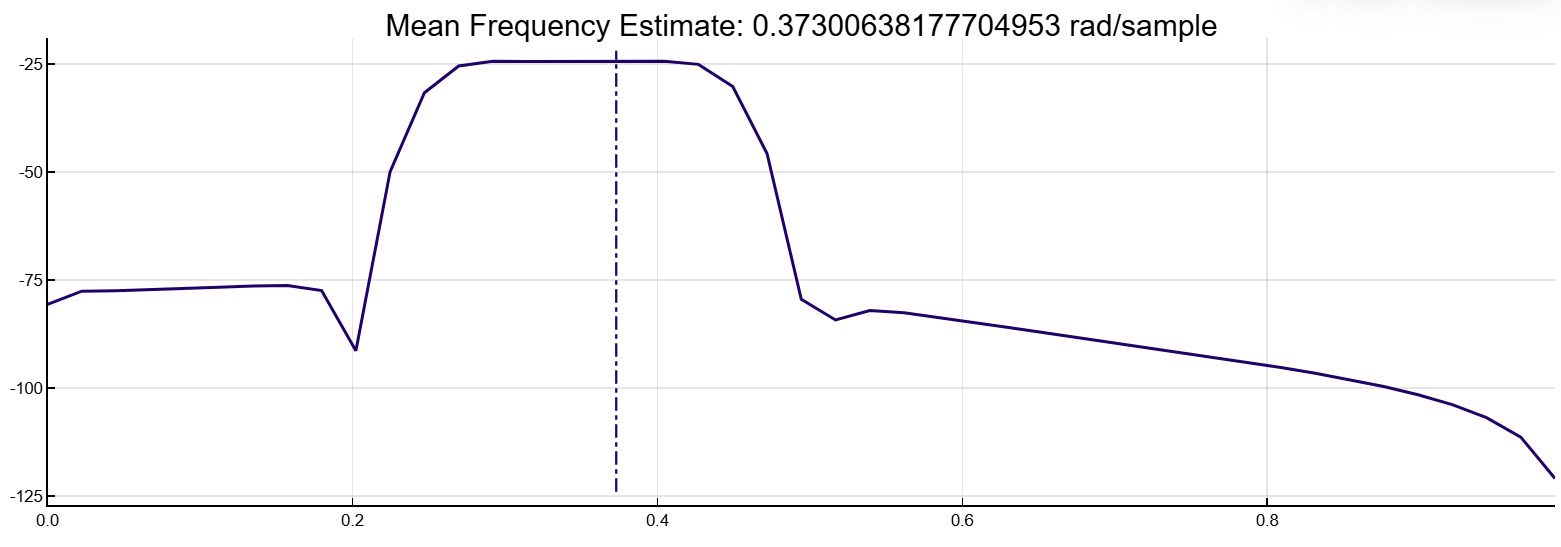

meanfreq 7

Выведем среднюю частоту и мощность для интервала измерения. Указание частоты дискретизации 2π эквивалентно тому, что частота дискретизации не задана.

mf=meanfreq(d,[],[0.3 0.6]*pi)
println("Mean = $(round(mf[1]/pi, digits=3))*pi, power = $(round(mf[2]/bandpower(d)*100, digits=1))% of total")

Mean = 0.373*π, power = 75.6% of total

Добавим второй канал с нормализованными частотами среза 0.5π рад/отсчет и 0.8π рад/отсчет и амплитудой, составляющей одну десятую от амплитуды первого канала.

d2=fir1(88,[0.5 0.8])/10
meanfreq([d d2],[],[0.3 0.9]*pi, out=:plot)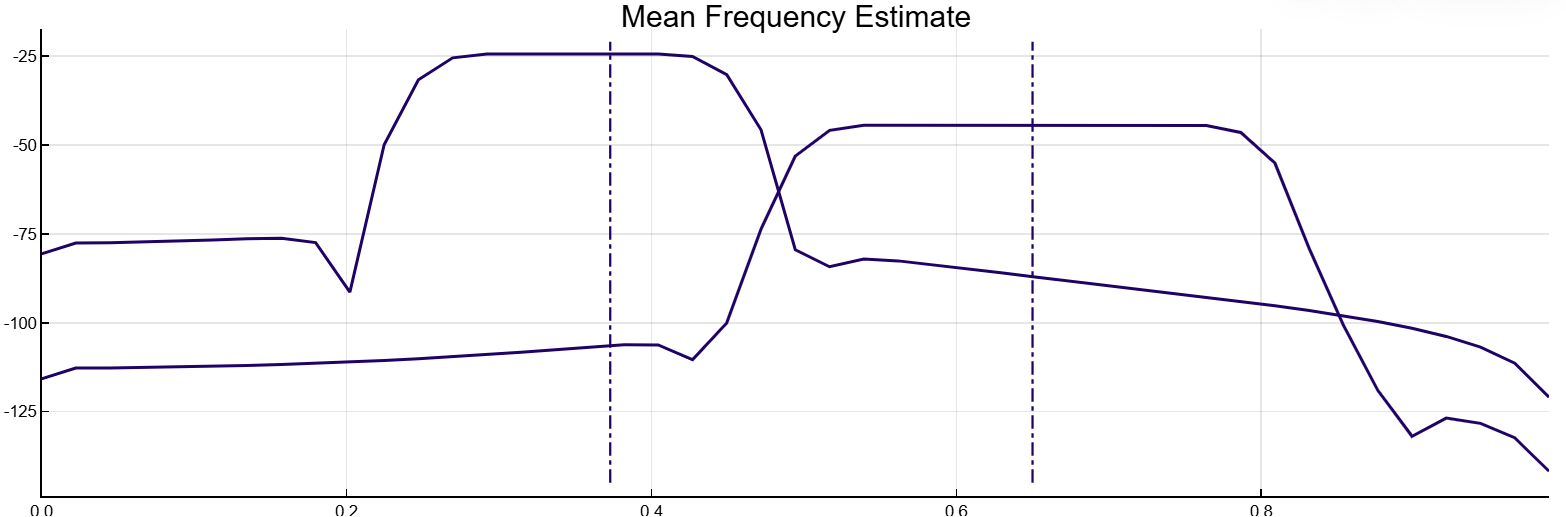

meanfreq 8

Выведем среднюю частоту каждого канала. Разделим на π.

mf=meanfreq([d d2],[],[0.3 0.9]*pi)
println(mf[1]/pi)

[0.3730065696360713 0.6500002992402633]

Алгоритмы

Details

Для определения средней частоты meanfreq вычисляет оценку спектра мощности периодограммы с помощью прямоугольного окна.

Одно и то же значение средней частоты mFrq можно получить из сигнала x с частотой дискретизации Fs тремя способами.

Непосредственно из сигнала	`mFrq = meanfreq(x,Fs)`
По периодограмме сигнала	`P,F = periodogram(x,[],length(x),Fs); mFrq = meanfreq(P,F)`
На основе оценки спектральной мощности сигнала (спектральной плотности мощности Уэлча)	`P,F = pwelch(x,rectwin(length(x)),[],length(x),Fs); mFrq = meanfreq(P,F)`

Поскольку meanfreq использует промежуточное представление для преобразования входного сигнала из временной области в частотную, возвращаемая средняя частота может меняться в зависимости от метода преобразования сигнала, количества точек ДПФ и размера окна.

Литература

Phinyomark, Angkoon, Sirinee Thongpanja, Huosheng Hu, Pornchai Phukpattaranont, and Chusak Limsakul, The Usefulness of Mean and Median Frequencies in Electromyography Analysis, Computational Intelligence in Electromyography Analysis – A Perspective on Current Applications and Future Challenges, edited by Ganesh R. Naik. London: IntechOpen, 2012. https://doi.org/10.5772/50639.