spectralFlatness
Спектральная неравномерность сигналов и спектрограмм.
| Библиотека |
|
Синтаксис
Вызов функции
-
flatness,arithmeticMean,geometricMean = spectralFlatness(x,f)— возвращает спектральную неравномерность, среднее арифметическое и среднее геометрическое спектральное значение сигналаxс течением времени. Интерпретацияxфункцией зависит от формыf.
-
flatness,arithmeticMean,geometricMean = spectralFlatness(x,f,Name,Value)— задает параметры с использованием одного или нескольких аргументов типа «имя-значение».
-
spectralFlatness(___;out=:plot)— строит график спектральной неравномерности.-
Если входной сигнал находится во временной области, график спектральной неравномерности строится в зависимости от времени.
-
Если входной сигнал находится в частотной области, график спектральной неравномерности строится в зависимости от номера кадра.
-
Аргументы
Входные аргументы
#
f —
частота дискретизации или вектор частот (Гц)
скаляр | вектор
Details
Частота дискретизации или вектор частот в Гц, заданные как скаляр или вектор соответственно. Интерпретация x функцией зависит от формы f:
-
Если
f— скаляр,xинтерпретируется как сигнал во временной области, аf— как частота дискретизации. В этом случаеxдолжен быть вещественным вектором или матрицей. Еслиxзадан как матрица, столбцы интерпретируются как отдельные каналы. -
Если
f— вектор,xинтерпретируется как сигнал в частотной области, аf— как частоты в Гц, соответствующие строкамx. В этом случаеxдолжен быть вещественным массивом размером , где — количество спектральных значений на заданных частотахf, — количество отдельных спектров, а — количество каналов. -
Количество строк
x, , должно быть равно количеству элементовf.
| Типы данных |
|
Входные аргументы «имя-значение»
Укажите необязательные пары аргументов в виде Name,Value, где Name — имя аргумента, а Value — соответствующее значение. Аргументы типа «имя-значение» должны располагаться после других аргументов, но порядок пар не имеет значения.
Используйте запятые для разделения имени и значения, а Name заключите в кавычки.
Следующие аргументы типа «имя-значение» применяются, если x — сигнал во временной области. Если x — сигнал в частотной области, аргументы типа «имя-значение» игнорируются.
|
#
Window —
окно, применяемое во временной области
rectwin(round(f*0.03)) (по умолчанию) | вектор
Details
Окно, применяемое во временной области, заданное как вещественный вектор. Количество элементов вектора должно находиться в диапазоне [1,size(x,1)]. Количество элементов вектора также должно быть больше OverlapLength.
| Типы данных |
|
#
FFTLength —
количество элементов в ДПФ
numel(Window) (по умолчанию) | положительный целочисленный скаляр
Details
Количество элементов, используемых для вычисления ДПФ оконных входных выборок, заданное как положительный целочисленный скаляр. Если аргумент не задан, FFTLength по умолчанию равен количеству элементов в Window.
| Типы данных |
|
#
SpectrumType —
тип спектра
"power" (по умолчанию) | "magnitude"
Details
Тип спектра, заданный как "power" или "magnitude":
-
"power"— спектральная неравномерность рассчитывается для одностороннего спектра мощности; -
"magnitude"— спектральная неравномерность рассчитывается для одностороннего амплитудного спектра.
| Типы данных |
|
#
out —
тип выходных данных
:data (по умолчанию) | :plot
Details
Тип выходных данных:
-
:data— функция возвращает данные; -
:plot— функция возвращает график.
Выходные аргументы
#
arithmeticMean —
среднее арифметическое спектра
скаляр | вектор | матрица
Details
Среднее арифметическое спектра, возвращаемое в виде скаляра, вектора или матрицы. Каждая строка arithmeticMean соответствует среднему арифметическому спектра окна x. Каждый столбец arithmeticMean соответствует независимому каналу.
#
geometricMean —
среднее геометрическое спектра
скаляр | вектор | матрица
Details
Среднее геометрическое спектра, возвращаемое в виде скаляра, вектора или матрицы. Каждая строка geometricMean соответствует среднему геометрическому спектра окна x. Каждый столбец geometricMean соответствует независимому каналу.
Примеры
Спектральная неравномерность сигнала во временной области
Details
Создадим ЛЧМ-сигнал с белым гауссовским шумом и рассчитаем неравномерность, используя параметры по умолчанию.
import EngeeDSP.Functions: chirp, randn, spectralFlatness
fs = 1000
t = (0:1/fs:10)
f1 = 300
f2 = 400
x = chirp(t, f1, 10, f2) + randn(length(t), 1)
flatness = spectralFlatness(x, fs)Построим график зависимости спектральной неравномерности от времени.
spectralFlatness(x, fs, out=:plot)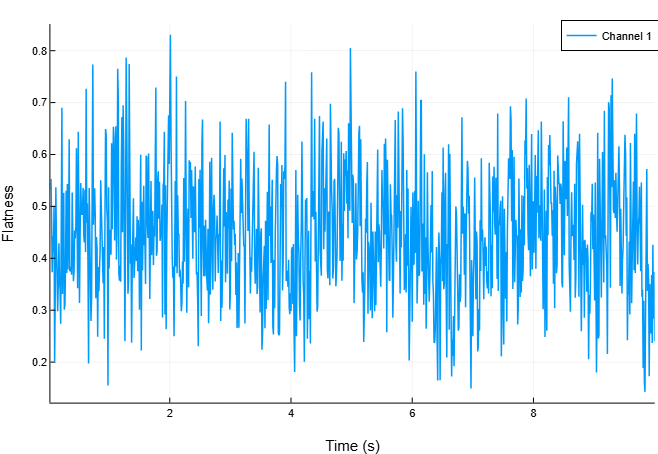
([0.5327040255782655, 0.552964530108542, 0.47742468036057234, 0.37293317041480095, 0.44287635975879003, 0.4119379715559745, 0.5013730779675295, 0.2015608067144641, 0.33548839011069864, 0.5369805014970516 … 0.1727536936022771, 0.35070131234444546, 0.25693379071386535, 0.255058829804521, 0.3677277425236599, 0.23687507452160672, 0.42585525405176444, 0.2835981233091784, 0.37349949783684333, 0.24033135785583964], [0.07786759765793372, 0.08135374655336428, 0.08637079824524838, 0.11933620888263814, 0.12350546278299357, 0.14497737376909484, 0.15042289056894764, 0.16892023682888072, 0.13419976354764332, 0.09558842868870962 … 0.10961556063903502, 0.11750795091292063, 0.10693418095926478, 0.09961268609163781, 0.10747394543349716, 0.15058502472661675, 0.14519245631195274, 0.15333273649350335, 0.13430846482161657, 0.12333737035602271], [0.04148038273449001, 0.04498573623545049, 0.04123555074472519, 0.04450443072388517, 0.05469764976765691, 0.05972168527195327, 0.07541798764132614, 0.03404769920562753, 0.04502246262583528, 0.05132912237457844 … 0.018936492976677682, 0.041210192596067945, 0.027475004470746342, 0.025407095148218223, 0.03952115133437092, 0.035669838953955334, 0.06183097036912634, 0.04348487631141832, 0.050164144166111126, 0.029641837692031523], Plot{Plots.PlotlyJSBackend() n=1})Спектральная неравномерность сигнала в частотной области
Details
Создадим ЛЧМ-сигнал с белым гауссовским шумом, а затем рассчитаем спектрограмму с помощью функции stft.
import EngeeDSP.Functions: chirp, randn, stft
fs = 1000
t = (0:1/fs:10)
f1 = 300
f2 = 400
x = chirp(t, f1, 10, f2) + randn(length(t), 1)
s, f = stft(x, fs, "FrequencyRange", "onesided")
s = abs.(s).^2Рассчитаем неравномерность спектрограммы с течением времени.
import EngeeDSP.Functions: spectralFlatness
flatness = spectralFlatness(s, f)Построим график зависимости спектральной неравномерности от номера кадра.
spectralFlatness(s, f, out=:plot)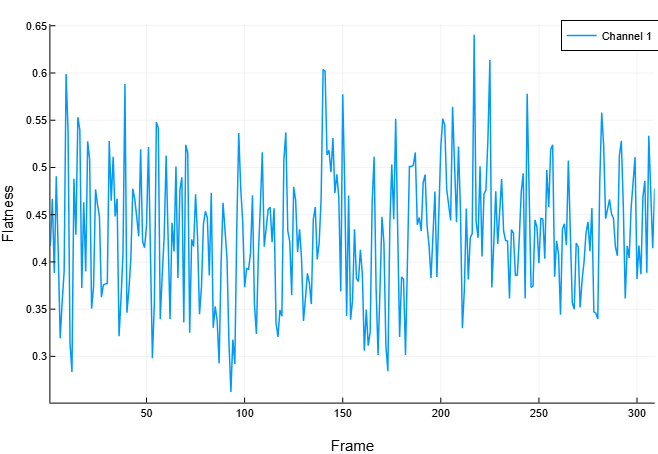
([0.41698805310198656, 0.46683201868098656, 0.3883287575836514, 0.4907688270016035, 0.4091462305599816, 0.3191585704065677, 0.3577051127741075, 0.3896555430416278, 0.598856100869491, 0.5385492705509978 … 0.3819877611783831, 0.41721990894367383, 0.38697190520523694, 0.46858320991071867, 0.48587071241197366, 0.38864151988166845, 0.5335128495308832, 0.4664062512134147, 0.4145737219480951, 0.477601293218658], [66.18935543214769, 71.25953873838431, 67.29284380517325, 72.27692418494, 77.76383362649338, 74.80810295770037, 65.91505570861669, 67.23287211343407, 73.51318020109804, 61.9977680185544 … 67.19403006538472, 79.16107520226234, 79.39008525296707, 70.97130285799408, 68.37996747931281, 63.08170611779957, 68.8590471648835, 79.56916556123606, 53.21814023726604, 53.157840474425484], [27.600170457726666, 33.26623431951591, 26.13174642913364, 35.47126130152683, 31.81677940217331, 23.87564719480698, 23.578152435762313, 26.197661293608466, 44.02381645774584, 33.38885274218245 … 25.667297109229274, 33.02757658777121, 30.721732544746853, 33.255960904744626, 33.22382351388131, 24.51617014235037, 36.73718646891848, 37.111556221595656, 22.062842473319066, 25.388253355296733], Plot{Plots.PlotlyJSBackend() n=1})Указание параметров, отличных от стандартных
Details
Создадим ЛЧМ-сигнал с белым гауссовским шумом.
import EngeeDSP.Functions: chirp, randn
fs = 1000
t = (0:1/fs:10)
f1 = 300
f2 = 400
x = chirp(t, f1, 10, f2) + randn(length(t), 1)Рассчитаем неравномерность спектра мощности с течением времени. Рассчитаем неравномерность для окон Хэмминга длительностью 50 мс с перекрытием 25 мс. Используем диапазон от 62.5 Гц до fs/2 для расчета неравномерности.
import EngeeDSP.Functions: spectralFlatness, hamming
flatness = spectralFlatness(x, fs,
"Window", hamming(round(Int, 0.05*fs)),
"OverlapLength", round(Int, 0.025*fs),
"Range", [62.5, fs/2])Построим график зависимости неравномерности от времени.
spectralFlatness(x, fs,
"Window", hamming(round(Int, 0.05*fs)),
"OverlapLength", round(Int, 0.025*fs),
"Range", [62.5, fs/2],
out=:plot)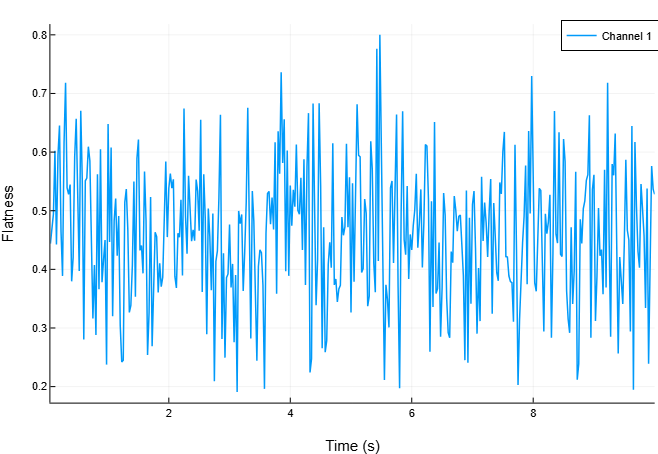
([0.44393966543497354, 0.4695783799925332, 0.49431342254249894, 0.6021106597242966, 0.44236146074090665, 0.5951722206261713, 0.6452967394540707, 0.46437619283350273, 0.3888478354209635, 0.6150829750332204 … 0.5454458473997145, 0.5030744478476047, 0.45828271847210195, 0.3342891893548354, 0.5377916650534941, 0.2390323362290697, 0.41558590905052906, 0.5762897059640517, 0.5368836411577717, 0.5281049952129195], [0.09501542410874092, 0.09365413839399048, 0.08501344767652717, 0.08096139641217256, 0.03234155232658504, 0.0508716873101426, 0.08013355128737082, 0.09856405316445577, 0.0713312402132862, 0.08216872345317404 … 0.09695049793640315, 0.0824351178183989, 0.1008633635765253, 0.09848674637522525, 0.0885626532954448, 0.08363028719440331, 0.10550801325677596, 0.08844347795474994, 0.06239257287735799, 0.1156749436919185], [0.042181115589996564, 0.043977958586646555, 0.0420232882831218, 0.04874771980593352, 0.014306656329816626, 0.030277415103377784, 0.051709919366615946, 0.045770799758748926, 0.027736998354829127, 0.05054058287626024 … 0.052881246502745685, 0.041471001379743265, 0.04622393645409, 0.03292305460796933, 0.04762825677731257, 0.019990342927586273, 0.04384764360143251, 0.05096906590498093, 0.033497551707597585, 0.06108851558467535], Plot{Plots.PlotlyJSBackend() n=1})Алгоритмы
Спектральная неравномерность рассчитывается, как описано в [1]:
где
-
— спектральное значение в бине ;
-
и — границы полосы в бинах, по которым рассчитывается спектральная неравномерность.