Начало работы с решателями в Engee
Что такое решатель и для чего он нужен
Решатели — это инструменты для расчета динамического поведения моделей Engee. Выбор решателя и его настройки существенно влияют на точность итогового решения и скорость его получения. Неудачный вариант может и вовсе привести к некорректному решению. Не существует универсального решателя для всех задач, поэтому важно выбирать его с учетом целей моделирования и особенностей модели.
|
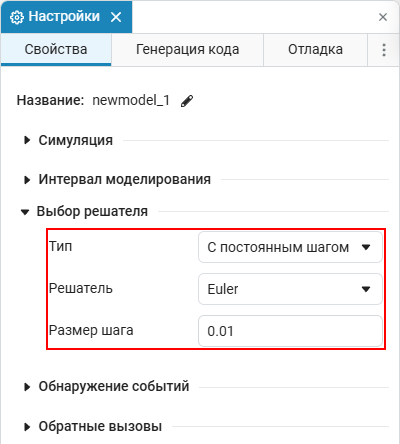
Чтобы посмотреть текущий решатель или выбрать другой, откройте окно Настройки
|
В первую очередь необходимо выбрать тип решателя:
-
С постоянным шагом — шаг остается неизменным на всем протяжении вычислительного эксперимента. Обычно используются для расчетов в реальном времени или проверки корректности численного решения. В общем случае являются неэффективными из-за того, что шаг на всем интервале моделирования оказывается ограничен требованиями отдельных более динамичных участков. Уменьшение до определенного предела шага позволяет повысить точность решения, но закономерно отрицательно сказывается на скорости расчета;
-
С переменным шагом — автоматически подстраивают величину шага по ходу вычислительного эксперимента, учитывая изменения в решении и оценки локальных ошибок интегрирования. Такие решатели уменьшают шаг в сложных областях для поддержания точности и увеличивает его в простых, чтобы ускорить расчеты.
Решатели также делятся на дискретные и непрерывные. Для моделей без непрерывных состояний (не имеющих в своем составе непрерывных интеграторов, передаточных функций и т.д.) — используются дискретные решатели, в иных случаях непрерывные. Если для модели без непрерывных состояний выбрать один из непрерывных решателей, то для эффективности он автоматически будет заменен на дискретный постоянного или переменного шага в соответствии с первоначальным выбором. Попытка посчитать дискретным решателем модель с непрерывными состояниями приведет к ошибке при запуске расчета.
Непрерывные решатели могут быть основаны на численных методах различных типов, среди которых отдельно стоит выделить:
-
Неявные методы — требуют решения системы нелинейных алгебраических уравнений на каждом шаге. Они подходят для жестких систем (подробнее см. в разделе Выбор решателя), так как позволяют использовать большие шаги без потери устойчивости, но каждый шаг требует серьезных вычислительных ресурсов. Примеры в Engee: ImplicitEuler, Trapezoid, TRBDF2, RadauIIA5, KenCarp*, Kvaerno*, QNDF*, QBDF*, FBDF;
-
Полуявные методы — в отличие от неявных требуют решения уже системы линейных алгебраических уравнений на каждом шаге. Как и неявные, хорошо подходят для жестких систем уравнений. В общем случае сильно зависят от точности расчета матрицы Якоби. Примеры в Engee: Rosenbrock*, Rodas*;
-
Многошаговые методы — используют данные с нескольких предыдущих шагов для расчета следующего. Они могут быть особенно эффективны для больших задач, но при наличии множественных событий их скорость работы падает из-за постоянных реинициализаций, поэтому их не рекомендуется использовать для моделей с разрывными компонентами. Примеры в Engee: VCABM*, AB*, ABM*, QNDF*, QBDF*, FBDF.
* — семейство методов, например, Kvaerno* означает Kvaerno3, Kvaerno4, Kvaerno5 и т.д.
Выбор решателя
При расчете модели нельзя одновременно достичь высоких точности и скорости. Необходимо найти баланс между этими показателями, выбрав подходящий решатель. Для этого потребуется иметь хорошее представление о характеристиках системы, которую он будет решать, а именно:
-
Жесткость системы — жесткой называют модель, в которой одновременно происходят быстрые и медленные процессы, как, например, в химических реакциях или электромеханических системах. Для таких моделей явные методы из-за своей малой области устойчивости требуют очень маленьких шагов, поэтому лучше использовать неявные или полуявные методы, шаг которых будет ограничен только требованиями точности. Система считается жесткой, если ее постоянные времени различаются на
6и более порядков; -
Размер модели — количество непрерывных переменных, уникально идентифицирующих конкретное состояние модели. Модель считается большой, если у нее более
1000переменных состояния. Чем их больше, тем медленнее идут расчеты, особенно при использовании неявных и полуявных методов. Для больших моделей лучше использовать методы с меньшим количеством расчетов правой части (производных системы) на каждом шаге; -
Требования к точности решения — определяют близость численного и точного решений. Отдельно выделяют требования к абсолютной и относительной точности:
-
Абсолютная точность (atol) — если переменная по модулю меньше этой уставки, оценка локальной ошибки для переменной считается нулевой. Например, для моделей с компонентами решения первого порядка обычно используют значение , но в общем случае эта уставка индивидуальна для каждой конкретной модели;
-
Относительная точность (rtol) — определяет допустимую локальную ошибку относительно самого значения переменной. Ориентировочные значения уставки:
-
— низкая точность;
-
— высокая точность;
-
— очень высокая точность.
Более высокая точность требует использования продвинутых решателей, что может заметно увеличить общее время расчетов.
-
-
-
Наличие разрывов в решении — некоторые библиотечные компоненты, например Модуль или Насыщение, характеризуются резкими скачкообразными изменениями поведения, что приводит к появлению разрывов в решении. Многошаговые методы в общем случае оказываются менее эффективны для таких задач.
В качестве отправной точки при выборе решателя с переменным шагом можно использовать следующую таблицу:
| Точность/жесткость | Нежесткая | Умеренной жесткости | Жесткая |
|---|---|---|---|
Низкая |
BS3 |
ROCK2 |
ImplicitEuler, Trapezoid, Rodas3, Rosenbrock23, TRBDF2 Большая размерность: TRBDF2 |
Средняя |
Tsit5, BS5, DP5 Большая размерность: VCABM |
ROCK4 |
Rodas4, Rodas4p, KenCapr4 Большая размерность: QNDF, QBDF |
Высокая |
DP8, Vern6, Vern7, Vern8, Vern9 Большая размерность: VCABM |
Rodas5, Rodas5p, RadauIIA5, Kvaerno5 |
Rodas5, Rodas5p, RadauIIA5, Kvaerno5 Большая размерность: QNDF, QBDF |
Поскольку универсального решателя для всех моделей не существует, то нужно самостоятельно подбирать решатель, ориентируясь на особенности задачи, требуемую точность и допустимое время вычислений. При этом можно пробовать не только решатели из одной ячейки (в таблице выше), но и из соседних, чтобы найти наиболее оптимальный вариант. Рациональным решением будет поиск баланса между производительностью и качеством, что позволит добиться корректного и эффективного моделирования.