Интегрирование на кольце
В этом примере мы исследуем интегрирование функции:
по кольцу, заданному , с параметром . Вычислим интеграл:
путем анализа функции в кольцевом полиномиальном ряду. Проанализируем функцию на сетке тензорного произведения , определяемой следующим образом:
преобразуем образцы функций в коэффициенты Чебышева-Фурье с помощью plan_annulus_analysis; и, наконец, мы преобразуем коэффициенты Чебышева-Фурье в кольцевые коэффициенты многочлена с помощью plan_ann2cxf.
Схему хранения массивов см. в этой документации.
using FastTransforms, LinearAlgebra, Plots
const GENFIGS = joinpath(pkgdir(FastTransforms), "docs/src/generated")
!isdir(GENFIGS) && mkdir(GENFIGS)
plotlyjs()Plots.PlotlyJSBackend()Наша функция в кольце:
f = (x,y) -> x^3/(x^2+y^2-1/4)#1 (generic function with 1 method)Степень кольцевого многочлена:
N = 8
M = 4N-329Внутренний кольцевой радиус:
ρ = 2/30.6666666666666666Радиальная сетка:
r = [begin t = (N-n-0.5)/(2N); ct = sinpi(t); st = cospi(t); sqrt(ct^2+ρ^2*st^2) end for n in 0:N-1]8-element Vector{Float64}:
0.9973277184004194
0.9763124517373388
0.9362410410518701
0.8811435628419545
0.8173313074308551
0.7535895152498838
0.7008983100472356
0.6706577864713554Угловая сетка (по модулю ):
θ = (0:M-1)*2/M0.0:0.06896551724137931:1.9310344827586206На отображаемой сетке тензорного произведения образцы функции имеют следующий вид:
F = [f(r*cospi(θ), r*sinpi(θ)) for r in r, θ in θ]8×29 Matrix{Float64}:
1.33215 1.24089 0.995869 0.672118 0.361447 0.136908 0.0255072 0.000211389 -0.00564085 -0.0675532 -0.235438 -0.509748 -0.838068 -1.13371 -1.30886 -1.30886 -1.13371 -0.838068 -0.509748 -0.235438 -0.0675532 -0.00564085 0.000211389 0.0255072 0.136908 0.361447 0.672118 0.995869 1.24089
1.32342 1.23275 0.989337 0.66771 0.359076 0.13601 0.0253399 0.000210003 -0.00560385 -0.0671101 -0.233894 -0.506405 -0.832572 -1.12628 -1.30028 -1.30028 -1.12628 -0.832572 -0.506405 -0.233894 -0.0671101 -0.00560385 0.000210003 0.0253399 0.13601 0.359076 0.66771 0.989337 1.23275
1.30981 1.22008 0.979168 0.660847 0.355385 0.134612 0.0250795 0.000207844 -0.00554625 -0.0664203 -0.23149 -0.5012 -0.824014 -1.1147 -1.28691 -1.28691 -1.1147 -0.824014 -0.5012 -0.23149 -0.0664203 -0.00554625 0.000207844 0.0250795 0.134612 0.355385 0.660847 0.979168 1.22008
1.29961 1.21057 0.97154 0.655698 0.352617 0.133563 0.0248841 0.000206225 -0.00550305 -0.0659028 -0.229687 -0.497295 -0.817594 -1.10601 -1.27689 -1.27689 -1.10601 -0.817594 -0.497295 -0.229687 -0.0659028 -0.00550305 0.000206225 0.0248841 0.133563 0.352617 0.655698 0.97154 1.21057
1.30613 1.21665 0.976415 0.658989 0.354386 0.134233 0.025009 0.00020726 -0.00553066 -0.0662336 -0.230839 -0.499791 -0.821697 -1.11156 -1.28329 -1.28329 -1.11156 -0.821697 -0.499791 -0.230839 -0.0662336 -0.00553066 0.00020726 0.025009 0.134233 0.354386 0.658989 0.976415 1.21665
1.34623 1.25399 1.00639 0.679218 0.365265 0.138354 0.0257767 0.000213622 -0.00570044 -0.0682668 -0.237925 -0.515133 -0.846922 -1.14569 -1.32269 -1.32269 -1.14569 -0.846922 -0.515133 -0.237925 -0.0682668 -0.00570044 0.000213622 0.0257767 0.138354 0.365265 0.679218 1.00639 1.25399
1.42719 1.32941 1.06692 0.720069 0.387234 0.146675 0.027327 0.00022647 -0.00604329 -0.0723726 -0.252235 -0.546115 -0.897858 -1.21459 -1.40224 -1.40224 -1.21459 -0.897858 -0.546115 -0.252235 -0.0723726 -0.00604329 0.00022647 0.027327 0.146675 0.387234 0.720069 1.06692 1.32941
1.5099 1.40645 1.12874 0.761795 0.409673 0.155175 0.0289105 0.000239594 -0.00639348 -0.0765664 -0.266852 -0.577762 -0.949887 -1.28498 -1.4835 -1.4835 -1.28498 -0.949887 -0.577762 -0.266852 -0.0765664 -0.00639348 0.000239594 0.0289105 0.155175 0.409673 0.761795 1.12874 1.40645Наложим график поверхности поверх сетки:
X = [r*cospi(θ) for r in r, θ in θ]
Y = [r*sinpi(θ) for r in r, θ in θ]
scatter3d(vec(X), vec(Y), vec(0F); markersize=0.75, markercolor=:red)
surface!(X, Y, F; legend=false, xlabel="x", ylabel="y", zlabel="f")
savefig(joinpath(GENFIGS, "annulus.html"))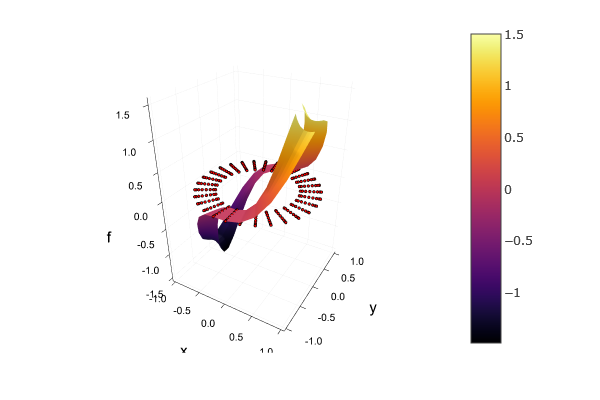
Предварительно вычислим план кольца — Чебышева-Фурье:
α, β, γ = 0, 0, 0
P = plan_ann2cxf(F, α, β, γ, ρ)FastTransforms Annulus--Chebyshev×Fourier plan for 8×29-element array of Float64И план анализа Чебышева-Фурье FFTW на кольце:
PA = plan_annulus_analysis(F, ρ)FastTransforms plan for FFTW Chebyshev×Fourier analysis on the annulus for 8×29-element array of Float64Его кольцевые коэффициенты:
U = P\(PA*F)8×29 Matrix{Float64}:
-1.22671e-17 2.92896e-17 0.926725 2.04896e-17 -7.722e-18 6.1888e-17 0.29418 -1.81602e-17 4.69005e-18 1.20498e-17 6.76339e-18 1.11857e-17 -1.99742e-17 -6.13512e-19 -4.02194e-17 6.23458e-17 3.04077e-17 3.12444e-17 -1.0558e-17 3.83711e-17 8.17668e-17 -1.08653e-17 5.99963e-17 -1.56088e-17 -4.23425e-17 -8.2245e-18 4.68313e-17 -3.30615e-17 -4.80225e-17
-5.57014e-18 -2.254e-18 -0.124037 -5.91733e-18 3.70137e-17 -1.89099e-17 -0.0976704 1.024e-18 -2.07932e-18 -9.77876e-18 1.98227e-17 -1.04302e-17 7.22713e-18 -5.50321e-18 4.99656e-17 -4.01755e-17 -1.81639e-17 -2.52689e-17 1.66849e-17 -2.67731e-17 -6.74982e-17 5.4336e-18 -6.11451e-17 1.0013e-17 2.95944e-17 7.96412e-18 -5.49385e-17 2.50418e-17 4.69813e-17
-2.33965e-17 1.12715e-18 0.042116 9.94105e-19 -1.44328e-17 9.15449e-18 0.0336531 3.6262e-19 1.34875e-17 7.39131e-18 -7.1196e-18 6.73552e-18 6.8403e-18 1.31493e-18 -1.89046e-17 2.30498e-17 5.34226e-18 1.03454e-17 -1.40577e-17 1.67754e-17 1.98659e-17 -8.57e-18 3.84689e-17 -1.14124e-17 -4.16632e-17 -5.45601e-18 3.66387e-17 -2.14064e-17 -4.31795e-17
2.21067e-18 4.00391e-18 -0.0139459 3.14722e-18 -1.97145e-18 5.82968e-18 -0.011224 6.26797e-18 2.18831e-17 6.88701e-18 -7.02346e-18 7.40166e-18 -2.2024e-18 9.55486e-18 4.62749e-18 2.9721e-18 -6.75798e-18 3.40533e-18 1.03823e-17 2.2961e-19 -1.52373e-17 7.73146e-18 -1.96827e-17 5.91455e-18 1.30222e-17 3.25478e-18 -1.53646e-17 8.18752e-18 6.59625e-18
-1.96208e-17 7.71573e-19 0.00458845 -2.03822e-18 1.86344e-17 3.19547e-18 0.00369818 -1.86152e-18 -3.29302e-18 8.11326e-19 -4.97022e-21 -1.77139e-18 1.47439e-18 -6.8012e-18 2.63512e-18 -4.24712e-18 5.7017e-18 -7.2048e-18 7.38785e-18 -4.72462e-18 1.59607e-17 -5.27319e-18 1.44348e-17 -1.67467e-18 -4.59916e-19 8.00009e-19 5.99498e-18 -3.34661e-18 -2.03062e-18
1.3498e-17 1.71852e-19 -0.00150441 7.97602e-19 -9.38596e-18 -3.21855e-18 -0.00121128 -4.47164e-19 -1.76175e-17 -4.83245e-18 6.52956e-18 -5.47568e-18 5.27089e-18 -2.9175e-18 5.23985e-18 -5.70705e-18 -3.147e-18 -3.85137e-19 -3.05417e-18 -5.31797e-19 -4.09175e-18 3.59849e-18 4.48894e-18 3.4972e-18 1.74387e-18 1.53405e-18 8.8938e-18 4.33464e-18 5.85819e-18
5.24011e-17 -4.20047e-18 0.000517281 -2.62968e-18 1.29799e-17 -9.06153e-18 0.000424358 -4.57265e-18 2.49476e-18 -6.80939e-18 -6.07451e-18 -2.399e-18 1.03771e-18 6.6648e-19 -1.96393e-17 1.69496e-20 -1.42128e-18 5.37575e-18 -1.16727e-17 3.57204e-19 -7.01129e-18 2.48838e-18 -1.17285e-17 4.39475e-19 5.83824e-18 -1.63971e-18 -3.91773e-19 1.39577e-18 1.02075e-17
-8.95802e-18 6.39707e-19 -0.000162126 3.55753e-18 7.44168e-18 4.28763e-18 -5.40419e-5 5.16629e-18 8.97839e-18 5.4486e-18 3.6724e-18 4.64571e-18 -1.67417e-18 6.04678e-19 5.73104e-18 -2.13942e-18 -1.44968e-17 -3.57457e-18 1.24167e-17 -5.67995e-18 -1.09651e-17 -4.98049e-18 6.22788e-18 -2.89642e-18 -1.52622e-17 -2.30036e-18 1.82749e-18 -1.26575e-18 -9.91876e-18Кольцевые коэффициенты полезны для интегрирования. Интеграл ^2] по кольцу приблизительно равен квадрату 2-нормы коэффициентов:
norm(U)^2, 5π/8*(1675/4536+9*log(3)/32-3*log(7)/32)(0.9735516844404257, 0.973547572736036)