Полуинтервальные многочлены Чебышева

В этой работе Даан Гюйбрехс (Daan Huybrechs) представил так называемые полуинтервальные многочлены Чебышева как полуклассические ортогональные многочлены относительно внутреннего произведения:

С помощью преобразования переменных полученные многочлены можно отнести к ортогональным многочленам в с весом Якоби , измененным весом .

Воспользуемся тем, что:

и результатами из этой работы, чтобы рассматривать полуинтервальные многочлены Чебышева как модификации многочленов Якоби .

using FastTransforms, LinearAlgebra, Plots, LaTeXStrings
const GENFIGS = joinpath(pkgdir(FastTransforms), "docs/src/generated")
!isdir(GENFIGS) && mkdir(GENFIGS)
plotlyjs()

Plots.PlotlyJSBackend()

Усечем производящую функцию, чтобы гарантировать относительную ошибку меньше eps() в равномерной норме для :

z = -1/(3+sqrt(8))
K = sqrt(-2z)
N = ceil(Int, log(abs(z), eps()/2*(1-abs(z))/K) - 1)
d = K .* z .^(0:N)

21-element Vector{Float64}:
  0.585786437626905
 -0.10050506338833466
  0.017243942703102998
 -0.0029585928302833363
  0.0005076142785970194
 -8.70928412987791e-5
  1.4942769195655289e-5
 -2.563773875152638e-6
  4.3987405526054037e-7
 -7.547045641060418e-8
  1.2948683203084688e-8
 -2.221642807903953e-9
  3.8117364433902886e-10
 -6.53990581302203e-11
  1.122070444229295e-11
 -1.925168523537399e-12
  3.303066989314436e-13
 -5.6671670051262317e-14
  9.723321376130305e-15
 -1.6682582055195078e-15
  2.862278569867433e-16

Затем преобразуем это представление в разложение в многочленах Якоби :

u = jac2jac(d, 0.0, 0.0, -0.5, 0.0; norm1 = false, norm2 = true)

21-element Vector{Float64}:
  0.9340010840223151
 -0.09412895357801879
  0.012332003442981326
 -0.0017749924171044493
  0.00026739546832682813
 -4.137724994351243e-5
  6.516867953544994e-6
 -1.0393137552650633e-6
  1.673019401749671e-7
 -2.7126077156467505e-8
  4.423525597533419e-9
 -7.247452797834485e-10
  1.1920483520702293e-10
 -1.9671182646957104e-11
  3.2552876283504113e-12
 -5.400110170678753e-13
  8.977555063800248e-14
 -1.4948797757615094e-14
  2.4980123321513196e-15
 -4.125155260660654e-16
  7.540496818753807e-17

Наша рабочая степень многочлена будет следующей:

n = 100

Вычислим коэффициенты связности между измененными ортогональными многочленами и многочленами Якоби:

P = plan_modifiedjac2jac(Float64, n+1, -0.5, 0.0, u)

FastTransforms Modified Jacobi--Jacobi plan for 101-element array of Float64

Сохраним связь с многочленами Чебышева первого рода:

P1 = plan_jac2cheb(Float64, n+1, -0.5, 0.0; normjac = true)

FastTransforms Jacobi--Chebyshev plan for 101-element array of Float64

Вычислим ряд Чебышева для измененного многочлена степени и его значения в точках Чебышева:

q = k -> lmul!(P1, lmul!(P, [zeros(k); 1.0; zeros(n-k)]))
qvals = k-> ichebyshevtransform(q(k))

#3 (generic function with 1 method)

Имея симметричную матрицу Якоби для и измененный план, можно вычислить измененную матрицу Якоби и соответствующие корни (как собственные значения):

XP = SymTridiagonal([-inv((4n-1)*(4n-5)) for n in 1:n+1], [4n*(2n-1)/(4n-1)/sqrt((4n-3)*(4n+1)) for n in 1:n])
XQ = FastTransforms.modified_jacobi_matrix(P, XP)
SymTridiagonal(XQ.dv[1:10], XQ.ev[1:9])

10×10 LinearAlgebra.SymTridiagonal{Float64, Vector{Float64}}:
 0.27324    0.615517     ⋅           ⋅            ⋅            ⋅            ⋅            ⋅            ⋅             ⋅
 0.615517  -0.0327708   0.509195     ⋅            ⋅            ⋅            ⋅            ⋅            ⋅             ⋅
  ⋅         0.509195   -0.0115134   0.50391       ⋅            ⋅            ⋅            ⋅            ⋅             ⋅
  ⋅          ⋅          0.50391    -0.00564494   0.502131      ⋅            ⋅            ⋅            ⋅             ⋅
  ⋅          ⋅           ⋅          0.502131    -0.00333235   0.501338      ⋅            ⋅            ⋅             ⋅
  ⋅          ⋅           ⋅           ⋅           0.501338    -0.00219677   0.500918      ⋅            ⋅             ⋅
  ⋅          ⋅           ⋅           ⋅            ⋅           0.500918    -0.00155663   0.500668      ⋅             ⋅
  ⋅          ⋅           ⋅           ⋅            ⋅            ⋅           0.500668    -0.00116057   0.500509       ⋅
  ⋅          ⋅           ⋅           ⋅            ⋅            ⋅            ⋅           0.500509    -0.000898551   0.5004
  ⋅          ⋅           ⋅           ⋅            ⋅            ⋅            ⋅            ⋅           0.5004       -0.000716244

И строим график:

x = (chebyshevpoints(Float64, n+1, Val(1)) .+ 1 ) ./ 2
p = plot(x, qvals(0); linewidth=2.0, legend = false, xlim=(0,1), xlabel=L"x",
         ylabel=L"T^h_n(x)", title="Half-Range Chebyshev Polynomials and Their Roots",
         extra_plot_kwargs = KW(:include_mathjax => "cdn"))
for k in 1:10
    λ = (eigvals(SymTridiagonal(XQ.dv[1:k], XQ.ev[1:k-1])) .+ 1) ./ 2
    plot!(x, qvals(k); linewidth=2.0, color=palette(:default)[k+1])
    scatter!(λ, zero(λ); markersize=2.5, color=palette(:default)[k+1])
end
p
savefig(joinpath(GENFIGS, "halfrange.html"))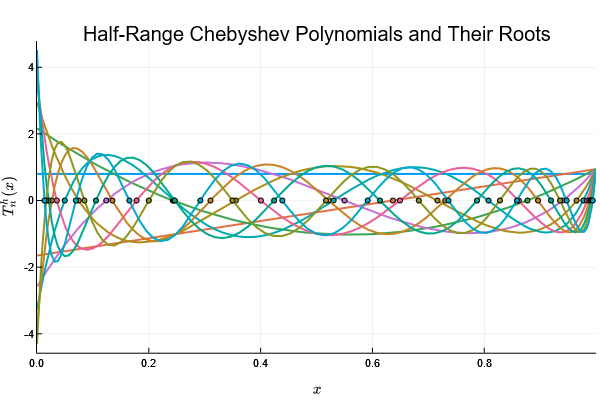

Согласно Theorem 2.20 получается, что производные полуинтервальных многочленов Чебышева являются линейной комбинацией не более чем двух многочленов, ортогональных относительно в точке . Это позволяет нам вычислить ленточную матрицу дифференцирования:

v̂ = 3*[u; 0]+XP[1:N+2, 1:N+1]*u
v = jac2jac(v̂, -0.5, 0.0, 0.5, 1.0; norm1 = true, norm2 = true)
function threshold!(A::AbstractArray, ϵ)
    for i in eachindex(A)
        if abs(A[i]) < ϵ A[i] = 0 end
    end
    A
end
P′ = plan_modifiedjac2jac(Float64, n+1, 0.5, 1.0, v)
DP = UpperTriangular(diagm(1=>[sqrt(n*(n+1/2)) for n in 1:n])) # Классическая матрица дифференцирования, представляющая _xD835__xDC9F_ P^{(-1/2,0)}(y) = P^{(1/2,1)}(y) D_P.
DQ = UpperTriangular(threshold!(P′\(DP*(P*I)), 100eps())) # Полуклассическая матрица дифференцирования, представляющая _xD835__xDC9F_ Q(y) = Q̂(y) D_Q.
UpperTriangular(DQ[1:10,1:10])

10×10 LinearAlgebra.UpperTriangular{Float64, Matrix{Float64}}:
 0.0  2.11682  0.481094  0.0       0.0      0.0       0.0       0.0       0.0       0.0
  ⋅   0.0      3.82901   0.789619  0.0      0.0       0.0       0.0       0.0       0.0
  ⋅    ⋅       0.0       5.53918   1.08781  0.0       0.0       0.0       0.0       0.0
  ⋅    ⋅        ⋅        0.0       7.24821  1.38334   0.0       0.0       0.0       0.0
  ⋅    ⋅        ⋅         ⋅        0.0      8.95658   1.67782   0.0       0.0       0.0
  ⋅    ⋅        ⋅         ⋅         ⋅       0.0      10.6646    1.97177   0.0       0.0
  ⋅    ⋅        ⋅         ⋅         ⋅        ⋅        0.0      12.3723    2.26542   0.0
  ⋅    ⋅        ⋅         ⋅         ⋅        ⋅         ⋅        0.0      14.0799    2.55888
  ⋅    ⋅        ⋅         ⋅         ⋅        ⋅         ⋅         ⋅        0.0      15.7874
  ⋅    ⋅        ⋅         ⋅         ⋅        ⋅         ⋅         ⋅         ⋅        0.0