PID Controller
PID 控制器。
blockType: PIDController
PID Controller 图书馆路径: |
|
Discrete PID Controller 图书馆路径: |
港口
输入
#
IN_1
—
输入信号
标量 | 向量 | 矩阵
Details
如下图所示,设定点与控制系统输出信号之间的差值:
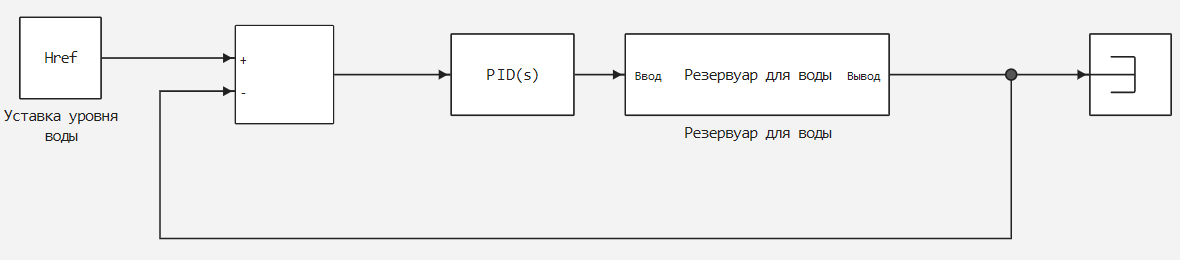
| 数据类型 |
Float16,Float32,Float64,Int8,Int16,Int32,Int64,UInt8,UInt16,UInt32,UInt64,Bool |
| 复数支持 |
无 |
输出
#
OUT_1
—
调节器输出
标量
Details
控制器输出是输入信号、输入信号积分和输入信号导数的加权和。求和权重由比例系数、积分系数和微分系数给出。求和中涉及哪些和取决于参数 Controller 的值。
当输入为矢量信号时,控制器的输出为矢量信号。在这种情况下,程序块就像 独立的 PID 控制器,其中 是输入矢量中的信号个数。
| 数据类型 |
Float64`。 |
| 复数支持 |
无 |
参数
主
#
Controller —
控制器类型
PID | PI | PD | P | I
Details
指定调节器的组成:
-
PID- 比例部分、积分部分和微分部分。 -
PI- 只有比例和积分部分。 -
PD- 仅比例和微分部分。 -
P- 只有比例部分。 -
I- 只计算积分部分。
| 值 |
|
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
无 |
#
Time domain —
离散或连续时间控制器
Discrete-time | Continuous-time
Details
对于值 `Discrete-time`建议明确指定程序块的计算步骤。选择值时 `Discrete-time`还包括参数 Integrator method 和 Filter method 。
当程序块 PID Controller 位于同步状态控制模型中时,不能选择 Continuous-time.
| 值 |
|
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
无 |
#
Sample time —
计算间隔
SampleTime (real number / vector of two real numbers)
Details
以非负数指定计算步骤之间的间隔。要继承一个计算步骤,请将此参数设置为 -1。
建议明确指定调节器计算步长,尤其是在后续区块的计算步长预计会发生变化的情况下。调节器系数 , , 和 的效果取决于计算步长。因此,对于一组给定的系数值,改变计算步骤会改变调节器的性能。
依赖关系
要使用该参数,请将 Time domain 设置为 Discrete-time.
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
是 |
#
Form —
调节器结构
Parallel | Ideal
Details
指定调节器结构是并联结构还是理想结构:
-
Parallel- 调节器的输出代表比例、积分和微分部分的总和,分别由 、 和 独立加权。例如,对于并联形式的连续时间 PID 控制器,传递函数的形式为.
对于离散时间的并行形式控制器,传递函数的形式为
,
其中,参数 Integrator method 和 Filter method 分别定义了 和 。
-
Ideal- 比例增益 作用于所有部分之和。例如,对于连续时间理想形式的 PID 控制器,传递函数的形式为对于离散时间的理想形式控制器,传递函数的形式为
,
其中,参数 Integrator method 和 Filter method 分别定义了 和 。
| 值 |
|
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
无 |
控制器参数
#
Proportional (P) —
比例系数
Real number
Details
按比例系数的有限实值。当 Form :
-
Parallel- 比例作用与积分和导数作用无关时。例如,对于连续时间的并行 PID 控制器,传递函数的形式为.
对于离散时间的并行形式控制器,传递函数的形式为
,
其中,参数 Integrator method 和 Filter method 分别定义了 和 。
-
Ideal- 比例系数 适用于所有部分的总和。例如,对于连续时间理想形式的 PID 控制器,传递函数的形式为.
对于离散时间的理想形式控制器,传递函数的形式为
,
其中,参数 Integrator method 和 Filter method 分别定义了 和 。
依赖关系
要使用该参数,请将 Controller 设置为 。 PID, PI, PD`或 `P.
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
是 |
#
Integral (I) —
积分因子
Real number
Details
积分系数的最终实数值。
依赖关系
要使用该参数,请将 Controller 设为 PID, PI`或 `I.
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
是 |
#
Derivative (D) —
微分系数
Real number
Details
微分系数的有限实数值。
依赖关系
要使用该参数,请将 Controller 设置为 PID`或 `PD.
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
是 |
#
Filter coefficient (N) —
导数的过滤系数
Real number
Details
滤波增益的有限实数值。滤波系数决定了块差分部分中滤波器极点的位置。滤波极点的位置取决于参数 Time domain 。
当 Time domain 设置为 Continuous-time`时,极点位置为 `s =−N。
当 Time domain 设置为 `Discrete-time`时,极点位置取决于参数 Filter method 。
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
是 |
#
Use filtered derivative —
滤取导数
Logical
Details
仅适用于时间离散的 PID 控制器:取消选中该复选框,将滤波导数替换为未滤波值。在这种情况下,控制器传递函数的微分项将变为
.
对于连续时间的 PID 控制器,导数部分总是经过滤波的。
依赖关系
要使用该参数,请将 Time domain 设置为 Discrete-time`并将 Controller 设置为 `PID`或 `PD.
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
无 |
积分器和滤波方法
#
Integrator method —
离散控制器中的积分方法
Forward Euler | Backward Euler | Trapezoidal
Details
在离散时间中,控制器传递函数的积分项等于 ,其中 取决于积分方法:
-
Forward Euler- 直接矩形(左手)近似:.
当奈奎斯特极限与控制器带宽相比较大时,这种方法最适合计算步长间隔较小的情况。对于较大的采样时间,该方法 `Forward Euler`会导致不稳定,即使在离散化系统在连续时间内是稳定的情况下也是如此。
-
Backward Euler- 反矩形(右旋)近似:.
该方法的优点是 `Backward Euler`的优势在于,使用这种方法对连续时间的稳定系统进行离散化处理,总能得到离散时间的稳定结果。
-
Trapezoidal- 双线性近似法.
该方法的优点是 `Trapezoidal`的优势在于,使用该方法对连续时间的稳定系统进行离散化处理,总能得到离散时间的稳定结果。在所有可用的积分方法中,该方法 `Trapezoidal`提供了离散化系统频域特性与相应连续时间系统特性之间最接近的对应关系。
依赖关系
要使用该参数,请将 Time domain 设置为 Discrete-time.
| 值 |
|
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
无 |
#
Filter method —
离散控制器中导数的计算方法
Forward Euler | Backward Euler | Trapezoidal
Details
在离散时间中,控制器传递函数的微分项等于
,
其中 取决于积分方法:
-
Forward Euler- 直接矩形(左手)近似法:.
当奈奎斯特极限与控制器带宽相比较大时,这种方法最适合计算步长间隔较小的情况。对于较大的采样时间,该方法 `Forward Euler`会导致不稳定,即使在离散化系统在连续时间内是稳定的情况下也是如此。
-
Backward Euler- 反矩形(右旋)近似:.
该方法的优点是 `Backward Euler`的优势在于,使用这种方法对连续时间的稳定系统进行离散化处理,总能得到离散时间的稳定结果。
-
Trapezoidal- 双线性近似法.
该方法的优点是 `Trapezoidal`的优势在于,使用该方法离散连续时间的稳定系统,总能得到离散时间的稳定结果。在所有可用的积分方法中,该方法 `Trapezoidal`提供了离散化系统频域特性与相应连续时间系统特性之间最接近的对应关系。
依赖关系
要使用该参数,请将 Time domain 设置为 Discrete-time.
| 值 |
|
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
无 |
参数
#
Differentiator initial condition —
导数的初始值
Real number
Details
导数的初始值。
依赖关系
要使用该参数,请将 Time domain 设置为 ,取消选中 ,并将 设置为 0。 Discrete-time,取消选中 Use filtered derivative ,并将 Controller 的值设置为 PID, PD.
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
是 |
#
Filter initial condition —
初始滤波值
Real number
Details
过滤器的初始值。
依赖关系
要使用此参数,请将 Time domain 设置为 ,选择 复选框,并将 设置为 0。 Discrete-time,选择 Use filtered derivative 复选框,并将 Controller 设置为 ,选择 复选框。 PID, PD.
或将 Time domain 设置为 Continuous-time, 并将 Controller 设置为 , , 并将 设置为 , 。 PID, PD.
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
是 |
#
Integrator initial condition —
积分器初始值
Real number
Details
积分器的初始值。
依赖关系
要使用该参数,请将 Controller 设为 PID, PI`或 `I.
| 默认值 |
|
| 程序使用名称 |
|
| 可调谐 |
无 |
| 可计算 |
是 |

