Engee documentation
Notebook

Processing the image of the starry sky and obtaining star coordinates

In this demonstration, we will show the development of an algorithm to detect the centroids of stars in an image and convert them to a spherical coordinate system.

The modular structure of Engee and the interactive script editor will allow us to quickly develop a prototype algorithm and evaluate its quality.

Input information for the algorithm

From a photograph of the starry sky, we will be able to calculate the orientation of the camera in celestial coordinate systems (e.g., equatorial). In doing so, we will have to create an image processing procedure that is insensitive to the various errors inherent in low-light photography on a moving platform. These include sensor thermal noise, image blurring, oversaturated pixels, backlighting by external sources, etc.

A useful source of starry sky images taken in all conditions is the project website https://nova.astrometry.net/

.

A typical frame from a star sensor looks as follows:

photo1713619559.jpeg

We see some noise, different brightness zones (sensor or primary processing errors), and motion blur. All this will not prevent us from finding the centroids of the stars, and then, knowing the camera parameters, determine the coordinates of each star in the spherical coordinate system attached to the camera.

In [ ]: 
Pkg.add(["Statistics", "ImageContrastAdjustment", "ImageSegmentation", "ImageBinarization", "ImageDraw", "IndirectArrays", "ImageFiltering", "ImageMorphology"])
In [ ]: 
# Установка библиотек: закомментируйте при повторном запуске
using Pkg; Pkg.add( [ "Images", "IndirectArrays", "ImageBinarization", "ImageContrastAdjustment", "ImageDraw", "ImageFiltering", "ImageMorphology", "FFTW",  ], io=devnull )

First of all - here is an abbreviated version of the code that we will get after all the tests.

In [ ]: 
using Images, ImageDraw, FileIO, FFTW, Statistics, IndirectArrays
using ImageBinarization, ImageContrastAdjustment, ImageFiltering, ImageMorphology
gr( leg=:false )

# Загрузка и предобработка
img = load( "photo1713619559.jpeg" )[1:end, 1:end-2]
img = binarize(img, MinimumError() ) 
#img = adjust_histogram( img, AdaptiveEqualization(nbins = 256, rblocks = 4, cblocks = 4, clip = 0.2))

# Сегментация
bw = Gray.(img) .> 0.7
labels = label_components( bw )
centers = component_centroids( labels )

# Первый график
src_img_temp = load( "photo1713619559.jpeg" )[1:end, 1:end-2]
[ draw!( src_img_temp, Ellipse(CirclePointRadius( Point(Int32.(round.([cy, cx]))...), 10; thickness = 5, fill = false)), RGB{N0f8}(1,0,0) ) for (cx,cy) in centers ]
p1 = plot( src_img_temp, showaxis=:false, grid=:false, ticks=:false, aspect_ratio=:equal )

# Второй график
(w,h), f = floor.(size(img)), 0.05
p2 = plot3d( camera=(60,20) )
for (cx,cy) in centers
    (scx,scy) = (.1 .* [w/h, 1] ./ 2) .* ([cx,cy] .- [w,h]./2) ./ [w,h]./2
    Pi = 1/(sqrt(scx^2 + scy^2 + f^2)) * [f; scy;-scx]
    plot!( p2, [0,Pi[1]], [0,Pi[2]], [0,Pi[3]], leg=:false, xlimits=(-0.1,1.1), ylimits=(-.3,.3), zlimits=(-.3,.3),
        showaxis=:true, grid=:true, ticks=:true, linealpha=.4, markershape=[:none, :star], markersize=[0, 2.5],
        title="Количество звезд: $(length(centers))", titlefontsize=10)
end

plot( p1, p2, size=(800,300) )
Out[0]:

Now let's analyse the individual steps of developing this algorithm.

Frame processing chain

The first thing we need to do is to process the frame. At each processing step we can apply several different algorithms, but it is always useful to break the task into several simpler subtasks, each of which requires different algorithms.

star_comp_vision_pipeline.svg

If the input is a correct frame (another algorithm should filter out blurred or overly blurred ones), then we have a few standard actions to perform:

  1. get rid of noise and binarise the image;
  2. segment the objects to work with them separately;
  3. translate their coordinates into the system we need.

In this example, we will only work with one specific image, which runs the risk of designing an algorithm that is too specialised. But this does not contradict our goal, as we only want to show the process of designing such an algorithm.

Preparing the environment

Let's install the necessary libraries. This step should be done once, uncomment it if some libraries are not loaded (by removing the # signs at the beginning of the line, or by highlighting the text and clicking Ctrl+/).

In [ ]: 
# using Pkg; Pkg.add( [ "Images", "IndirectArrays", "ImageBinarization", "ImageContrastAdjustment",
#                       "ImageDraw", "ImageFiltering", "ImageMorphology", "FFTW" ], io=devnull )
In [ ]: 
using Images, ImageDraw, ImageBinarization, ImageContrastAdjustment
using ImageSegmentation, ImageFiltering, ImageMorphology, IndirectArrays
using FileIO, FFTW

We will be building charts like heatmap and histogram, which are not very fast when applying the backend plotly(). Therefore, we will choose a backend that is not interactive, but faster, and at the same time we will set parameters common for all charts in advance.

In [ ]: 
gr( showaxis=:false, grid=:false, ticks=:false, leg=:false, aspect_ratio=:equal )
Out[0]:
Plots.GRBackend()

Since we will mainly work with images, we can disable the display of axes, coordinate grid, axis serifs and legend for all future graphs in advance, so that we don't have to do it for each graph separately.

Let's load the image

In [ ]: 
photoName = "photo1713619559.jpeg";
img = load( photoName )[1:end, 1:end-2];

Displaying the entire image would take up too much space on the canvas of the interactive script. In addition, we will have to evaluate how the processing affects individual groups of pixels, i.e. we will need to work with a large approximation.

Let's define two zones that we will be interested in and call it RoI (from Region of Interest, "area of interest"):

In [ ]: 
RoI = CartesianIndices( (550:800,450:850) );
RoI2 = CartesianIndices( (540:590, 590:660) );

Choosing an image binarisation algorithm

Let's use the commands from ImageBinarization and ImageContrastAdjustment libraries to get a black-and-white (or close to it) image on which it will be convenient to segment individual stars.

First of all, let's study the histogram of the image of the starry sky. Each planner will have its own set of filters to apply depending on noise and backlight conditions.

In [ ]: 
plot(
    plot( img[RoI], title="Фрагмент исходного изображения" ),
    histogram( vec(reinterpret(UInt8, img)), xlimits=(0,256), ylimits=(0,10), xticks=:true, yticks=:false, leg=:false, aspect_ratio=:none, title="Гистограмма"),
    plot( img[RoI2], title="Фрагмент (ближе)" ),
    size=(800,200), layout=grid(1,3, widths=(0.4,0.3,0.3)), titlefont=font(10) 
)
Out[0]:

On the histogram there are many pixels of grey shades (the area 50-100). Besides, we can see that there are compression artefacts on the image. Let's try to simply change the contrast of the image.

In [ ]: 
img = adjust_histogram( Gray.(img), ContrastStretching(t = 0.5, slope = 12) )

plot(
    plot( img[RoI], title="Фрагмент изображения после бинаризации и выравнивания гистограммы" ),
    histogram( vec(reinterpret(UInt8, img)), xlimits=(0,256), ylimits=(0,10), xticks=:true, yticks=:false, leg=:false, aspect_ratio=:none, title="Гистограмма"),
    plot( img[RoI2], title="Фрагмент (ближе)" ),
    size=(800,200), layout=grid(1,3, widths=(0.4,0.3,0.3)), titlefont=font(10) 
)
Out[0]:

The pixel density in the 50-100 region has become much lower, most pixels now have a brightness of 0-20, but we haven't lost any bright pixels. By trial and error we have found a simple and quite satisfactory preprocessing method that processes the whole image at once, solves the noise problem and allows us to proceed to binarisation.

However, as further experiments will show us, because we applied a global operation (to the whole image), some stars became almost invisible, or discontinuities appeared in the lines formed by motion blur.

What if binarisation by thresholding is enough? You can find another binarisation algorithm in documentation.

In [ ]: 
img = load( photoName )[1:end, 1:end-2]   # Загрузим изображение заново

img = binarize(img, MinimumError() )      # Бинаризация

plot(
    plot( img[RoI], title="Фрагмент исходного изображения" ),
    histogram( vec(reinterpret(UInt8, img)), xlimits=(0,256), ylimits=(0,10), xticks=:true, yticks=:false, leg=:false, aspect_ratio=:none, title="Гистограмма"),
    plot( img[RoI2], title="Фрагмент (ближе)" ),
    size=(800,200), layout=grid(1,3, widths=(0.4,0.3,0.3)), titlefont=font(10) 
)
Out[0]:

At this stage, we only need to avoid merging objects. Additional experiments, some operations (e.g, morphological from the library ImageMorphology) noticeably change the direction of lines on the frame and can change the coordinates of their centroids.

If some stars are not recognised or their morphology changes, we will be able to detect them at later stages, when comparing with the star catalogue, and to achieve sub-pixel accuracy of localisation of each star we can work on each found image separately.

Let us assume that we are satisfied with the image filtering algorithm. Let's move on to the next step - segmentation.

Segmentation

In this step we have to extract the centroids of the stars from the two-dimensional matrix of the stellar image. The simplest solution would be to blur the image and take the local maxima. However, to make it work, we will have to choose a lot of parameters and make sure that it is robust to interferences arising in each particular scenario of the algorithm application.

In [ ]: 
img = load( photoName )[1:end, 1:end-2]   # Загрузим изображение заново

# Бинаризация
img = binarize(img, MinimumError() );
# Гауссовский фильтр
img = imfilter(img, Kernel.gaussian(3));
# Найдем центры при помощи морфологической операции
img_map = Gray.( thinning( img .> 0.1 ) );
# Перечислим все пики их в массиве координат типа CartesianCoordinates
img_coords = findall( img_map .== 1);

# Выведем график
plot( img, title="Обнаружено звезд: $(length(img_coords))", titlefont=font(11) )
scatter!( last.(Tuple.(img_coords)), first.(Tuple.(img_coords)), c=:yellow, markershape=:star, markersize=4 )
Out[0]:

Not a bad result, though:

  • a few stars were not detected,
  • some stars were found to be connected to each other, which will lead to large errors when comparing with the star catalogue,
  • the operation thinning may return a smear trajectory rather than a point, and each smear line will be identified as a separate star.

The output of this procedure can be used as another metric of the quality of the preprocessing procedure.

Let us develop a reference procedure against which we will check the simplified solutions. If our objects overlapped, we could use the [watershed segmentation] method(https://ru.wikipedia.org/wiki/%D0%A1%D0%B5%D0%B3%D0%BC%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D0%B8%D1%8F_(%D0%BE%D0%B1%D1%80%D0%B0%D0%B1%D0%BE%D1%82%D0%BA%D0%B0_%D0%B8%D0%B7%D0%BE%D0%B1%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B9)#%D0%A1%D0%B5%D0%B3%D0%BC%D0%B5%D0%BD%D1%82%D0%B0%D1%86%D0%B8%D1%8F_%D0%BC%D0%B5%D1%82%D0%BE%D0%B4%D0%BE%D0%BC_%D0%B2%D0%BE%D0%B4%D0%BE%D1%80%D0%B0%D0%B7%D0%B4%D0%B5%D0%BB%D0%B0). Its implementation can be found in another demo: https://engee.com/helpcenter/stable/interactive-scripts/image_processing/Indexing_and_segmentation.html.

But since our objects do not overlap and are well distinguishable from each other, we will need the function label_components from ImageMorphology.

In [ ]: 
img = load( photoName )[1:end, 1:end-2]   # Повторим загрузку и предобработку
img = binarize(img, MinimumError() )

# Сегментация
bw = Gray.(img) .> 0.7;                     # Еще раз бинаризуем изображение (нам нужна маска)
labels = label_components( bw );            # Пронумеруем все связанные области (маркеры – целые числа)

From the object segments we can extract the areas, dimensions and coordinates of each object using the library functions ImageMorphology (such as component_boxes, component_centroids...).

In [ ]: 
# Центр каждого объекта
centers = component_centroids( labels );

To visually assess the quality of the algorithm's work, let's mark the detected objects on the graph.

In [ ]: 
src_img_temp = load( photoName )[1:end, 1:end-2]

for (cy,cx) in centers
    draw!( src_img_temp, Ellipse(CirclePointRadius(Int64(round(cx)), Int64(round(cy)), 10; thickness = 5, fill = false)), RGB{N0f8}(1,0,0) )
end

plot( src_img_temp, title="Обнаружено звезд: $(length(centers))", titlefont=font(11))
Out[0]:

To get a closer look at this graph, you can save it to a separate file.

In [ ]: 
save( "$(photoName)_detection.png", src_img_temp )

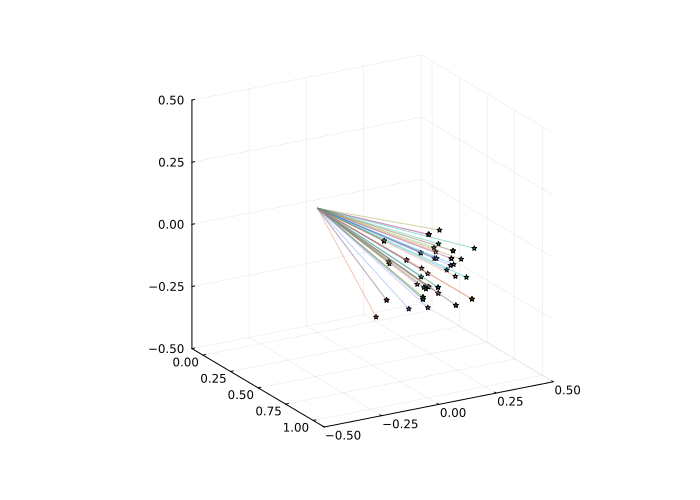
Determining star coordinates

The last step is to convert the coordinates of the stars into a spherical coordinate system. It is still tied to the camera axes, so we can call it the device coordinate system, not to confuse it with other coordinate systems - geocentric, equatorial, etc..

Using the formula from this article, we will project the pixels from the sensor coordinate system $m_i$ onto a unit sphere, on which the radius-vector of the real-world point $P_i$, which the camera has photographed, will be 1. The coordinates of the pixels will be set relative to the centre of the frame (w/2, h/2) by the variables $u_i$, $v_i$, the projective model also uses the focal length $f$.

$$P_i \rightarrow m_i = \frac{P_i}{\lVert P_i \rVert} = \frac{1}{\sqrt{u_i^2 + v_i^2 + f^2}} \begin{bmatrix} u_i\\ v_i\\ f \end{bmatrix}$$

Here we have chosen a realistic focal length (50 mm) but a completely unrealistic sensor size (10 cm on the long side), at least for modern embedded hardware. This is done for better visualisation.

In [ ]: 
f = .05; # Фокусное расстояние в метрах
w,h = floor.(size(img))
sensor_size = .1 .* [w/h, 1]

plot3d( )

# Обработаем все найденные центроиды звезд
for (cx,cy) in centers
    # Вычислим координаты пикселя в системе координат сенсора
    (scx,scy) = (sensor_size ./ 2) .* ([cx,cy] .- [w,h]./2) ./ [w,h]./2
    # Координаты точки на единичной сфере
    Pi = 1/(sqrt(scx^2 + scy^2 + f^2)) * [f; scy;-scx]
    # Выведем на графике очередной радиус-вектор
    plot!( [0,Pi[1]], [0,Pi[2]], [0,Pi[3]], leg=:false,
        xlimits=(-0.1,1.1), ylimits=(-.5,.5), zlimits=(-.5,.5),
        showaxis=:true, grid=:true, ticks=:true, linealpha=.4,
        markershape=[:none, :star], markersize=[0, 2.5])
end

plot!(size = (700,500), camera=(60,20) )
Out[0]:

We obtained a projection of the centroids of the stars onto a unit sphere in the instrumental coordinate system.

Conclusion

We managed to process the frame from the star sensor and translate the coordinates of stars from planar to spherical coordinate system. For this purpose we tried several algorithms already implemented in different libraries. The method of working on separate steps of the algorithm in separate code cells of the interactive script allowed us to perform a number of computational experiments faster, outputting very complex and clear illustrations, which accelerated the research process and allowed us to find a satisfactory solution to the problem of filtering a star image sooner.

After the costly prototyping stage, the algorithm could easily be translated into a more efficient form (e.g. rewritten in C/C++) and placed in a model-oriented environment as a block from which to generate code. Another direction for developing this work could be to develop a sensor error model, which could easily be embodied by standard directional blocks on the Engee canvas.