Осциллятор Ван дер Поля
В этом примере показано, как смоделировать дифференциальное уравнение Ван дер Поля (VDP) второго порядка в Engee. В динамике генератор неконсервативен и имеет нелинейное затухание. При больших амплитудах генератор рассеивает энергию. При малых амплитудах генератор генерирует энергию.
Осциллятор задается дифференциальным уравнением второго порядка:
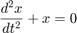
где:
- x — положение относительно времени.
- t - время
- Mu — затухание.
Генератор VDP используется в биологических и физических науках, в том числе в электрических цепях.
Далее перейдём к реализации – объявим функцию запуска модели и подключим необходимые библиотеки.
using Plots
function run_model(name_model)
Path = (@__DIR__) * "/" * name_model * ".engee"
if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
model = engee.open( name_model ) # Открыть модель
model_output = engee.run( model, verbose=true ); # Запустить модель
else
model = engee.load( Path, force=true ) # Загрузить модель
model_output = engee.run( model, verbose=true ); # Запустить модель
engee.close( name_model, force=true ); # Закрыть модель
end
return model_output
end
Запустим модель с несколькими вариантами значения Mu. Далее на рисунке можно увидеть модель, которую мы сделали на основе формулы, описанной выше.
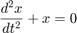
Коэффициент затухания равен единице
Зададим Mu и запустим модель, после чего проанализируем залогированные данные.
Mu = 1;
run_model("vdp")
sleep(5)
collect(simout)
# Скорость
v = simout["vdp/Integrator.1"];
v = collect(v);
plot(v.time, v.value)
# Положение
p = simout["vdp/Integrator-1.1"];
p = collect(p);
plot!(p.time, p.value)
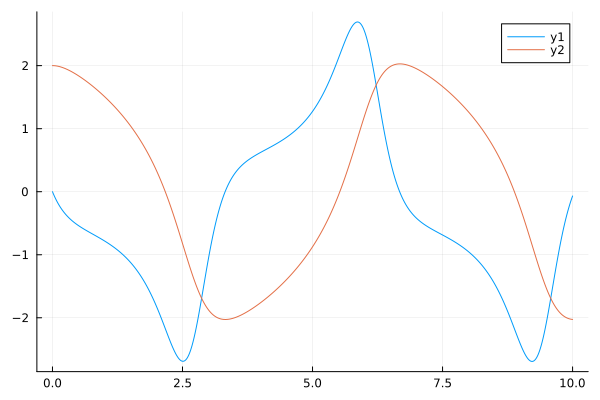
Как мы видим из результирующего графика, при Mu = 1 генератор VDP имеет нелинейное затухание.
Коэффициент затухания равен нулю
Зададим Mu и запустим модель, после чего проанализируем залогированные данные.
Mu = 0;
run_model("vdp")
sleep(5)
collect(simout)
# Скорость
v = simout["vdp/Integrator.1"];
v = collect(v);
plot(v.time, v.value)
# Положение
p = simout["vdp/Integrator-1.1"];
p = collect(p);
plot!(p.time, p.value)
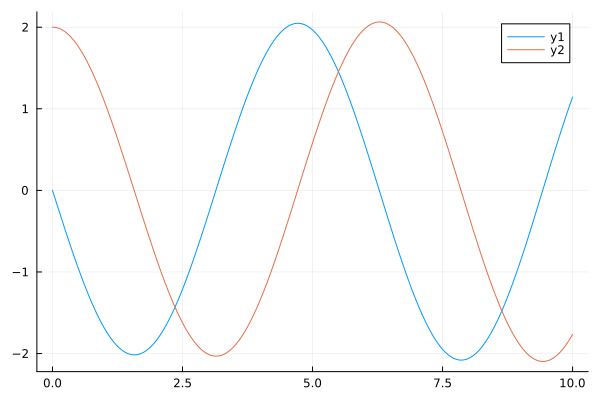
Анализируя график, мы можем сделать вывод, что при Mu = 0 генератор VDP не имеет затухания, энергия сохраняется, и само дифференциальное уравнение приобретает следующий вид:
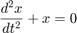
Вывод
В данном примере мы смоделировали дифференциальное уравнение Ван дер Поля второго порядка в Engee и посмотрели, как оно работает с различными значениями коэффициента затухания.