Документация Engee

bandpass

Страница в процессе разработки.

Сигналы после полосового фильтра.

Библиотека

EngeeDSP

Синтаксис

Вызов функции

  • y = bandpass(x,wpass) — фильтрует входной сигнал x с помощью полосового фильтра с диапазоном частот полосы пропускания, заданным двухэлементным вектором wpass в нормированных единицах рад/отсчет. Функция bandpass использует фильтр минимального порядка с затуханием в полосе пропускания 60 дБ и компенсирует задержку, вносимую фильтром. Если x - матрица, то функция фильтрует каждый столбец независимо.

  • y = bandpass(x,fpass,fs) — использует частоту дискретизации fs в Гц входного сигнала x. Двухэлементный вектор fpass задает диапазон частот полосы пропускания фильтра в Гц.

  • y = bandpass(___, Name,Value) — задает дополнительные опции для любого из предыдущих синтаксисов одним или несколькими аргументами Name,Value.

  • y = bandpass(___; out=:plot) — строит график входного сигнала и накладывает отфильтрованный сигнал.

Аргументы

Входные аргументы

# x — входной сигнал
вектор | матрица

Details

Входной сигнал, заданный как вектор или матрица.

Типы данных

Float32, Float64
Поддержка комплексных чисел

Да

# wpass — нормированный диапазон частот полосы пропускания
двухэлементный вектор с элементами в интервале (0, 1)

Details

Нормированный диапазон частот полосы пропускания, заданный в виде двухэлементного вектора с элементами в интервале (0, 1).

# fpass — диапазон частот полосы пропускания, Гц
двухэлементный вектор с элементами в интервале (0, fs/2)

Details

Диапазон частот полосы пропускания, заданный в виде двухэлементного вектора с элементами в интервале (0, fs/2) в Гц.

# fs — частота дискретизации
скаляр

Details

Частота дискретизации, заданная как положительный вещественный скаляр.

Входные аргументы «имя-значение»

Укажите необязательные пары аргументов в формате Name, Value, где Name — имя аргумента, а Value — соответствующее значение. Аргументы типа «имя-значение» должны располагаться после других аргументов, но порядок пар не имеет значения.

Используйте запятые для разделения имени и значения, а Name заключите в кавычки.

Пример: f=bandpass(x, 200, fs, "StopbandAttenuation",30).

# ImpulseResponse — тип импульсной характеристики
"auto" (по умолчанию) | "fir" | "iir"

Details

Тип импульсной характеристики фильтра, заданный как "fir", "iir" или "auto":

  • "fir" — функция проектирует фильтр минимального порядка, линейно-фазовый, с конечной импульсной характеристикой (КИХ). Чтобы компенсировать задержку, функция добавляет к входному сигналу нулей, где — порядок фильтра. Затем функция фильтрует сигнал и удаляет первые отсчетов на выходе.

    В этом случае входной сигнал должен быть как минимум в два раза длиннее, чем фильтр, удовлетворяющий спецификациям.

  • "iir" — функция проектирует фильтр минимального порядка с бесконечной импульсной характеристикой (БИХ) и использует функцию filtfilt для выполнения фильтрации с нулевой фазой и компенсации задержки фильтра.

    Если сигнал не в три раза длиннее, чем фильтр, удовлетворяющий спецификации, функция проектирует фильтр меньшего порядка и, следовательно, меньшей крутизны.

  • "auto" — функция проектирует КИХ-фильтр минимального порядка, если входной сигнал достаточно длинный, и БИХ-фильтр минимального порядка в противном случае. В частности, функция выполняет следующие шаги:

    • Вычисляет минимальный порядок, который должен иметь КИХ-фильтр, чтобы соответствовать спецификациям. Если сигнал как минимум вдвое длиннее требуемого порядка фильтра, проектирует и использует этот фильтр.

    • Если сигнал недостаточно длинный, вычисляет минимальный порядок, который должен иметь КИХ-фильтр, чтобы соответствовать спецификациям. Если длина сигнала по крайней мере в три раза превышает требуемый порядок фильтра, проектирует и использует этот фильтр.

    • Если длина сигнала недостаточна, урезает порядок до одной трети длины сигнала и проектирует БИХ-фильтр такого порядка. Уменьшение порядка происходит за счет крутизны спада переходной полосы.

    • Фильтрует сигнал и компенсирует задержку.

# Steepness — крутизна спада переходной полосы
[0.85 0.85] (по умолчанию) | двухэлементный вектор с элементами в интервале [0.5, 1) | скаляр в интервале [0.5, 1)

Details

Крутизна спада переходной полосы, заданная как двухэлементный вектор с элементами в интервале [0.5, 1) или скаляр в интервале [0.5, 1). По мере увеличения крутизны импульсная характеристика фильтра приближается к идеальной импульсной характеристике полосового фильтра, но при этом увеличивается и результирующая длина фильтра, а также вычислительные затраты на операцию фильтрации. Дополнительную информацию см. в разделе Крутизна спада полосового фильтра.

# StopbandAttenuation — затухание в полосе задерживания фильтра
60 (по умолчанию) | положительный скаляр в дБ

Details

Затухание в полосе задерживания фильтра, заданное как положительный скаляр в дБ.

Выходные аргументы

# y — отфильтрованный сигнал
вектор | матрица

Details

Отфильтрованный сигнал, возвращаемый в виде вектора или матрицы с теми же размерами, что и входной сигнал.

Примеры

Полосовая фильтрация тонов

Details

Сгенерируем сигнал, дискретизированный с частотой 1 кГц в течение 1 секунды. Сигнал содержит три тона: с частотой 50 Гц, 150 Гц и 250 Гц. Амплитуда высокочастотного и низкочастотного тона вдвое больше амплитуды промежуточного тона. К сигналу добавлен гауссовский белый шум с дисперсией 1/100.

import EngeeDSP.Functions: bandpass, randn

fs = 1e3
t = 0:1/fs:1
x = [2 1 2] * sin.(2π * [50; 150; 250] .* reshape(t, 1, :)) + randn(1, length(t)) / 10

Отфильтруем сигнал с помощью полосового фильтра, чтобы удалить низкочастотные и высокочастотные составляющие. Укажем частоты полосы пропускания 100 Гц и 200 Гц. Выведем исходный и отфильтрованный сигналы, а также их спектры.

bandpass(x,[100 200],fs; out=:plot)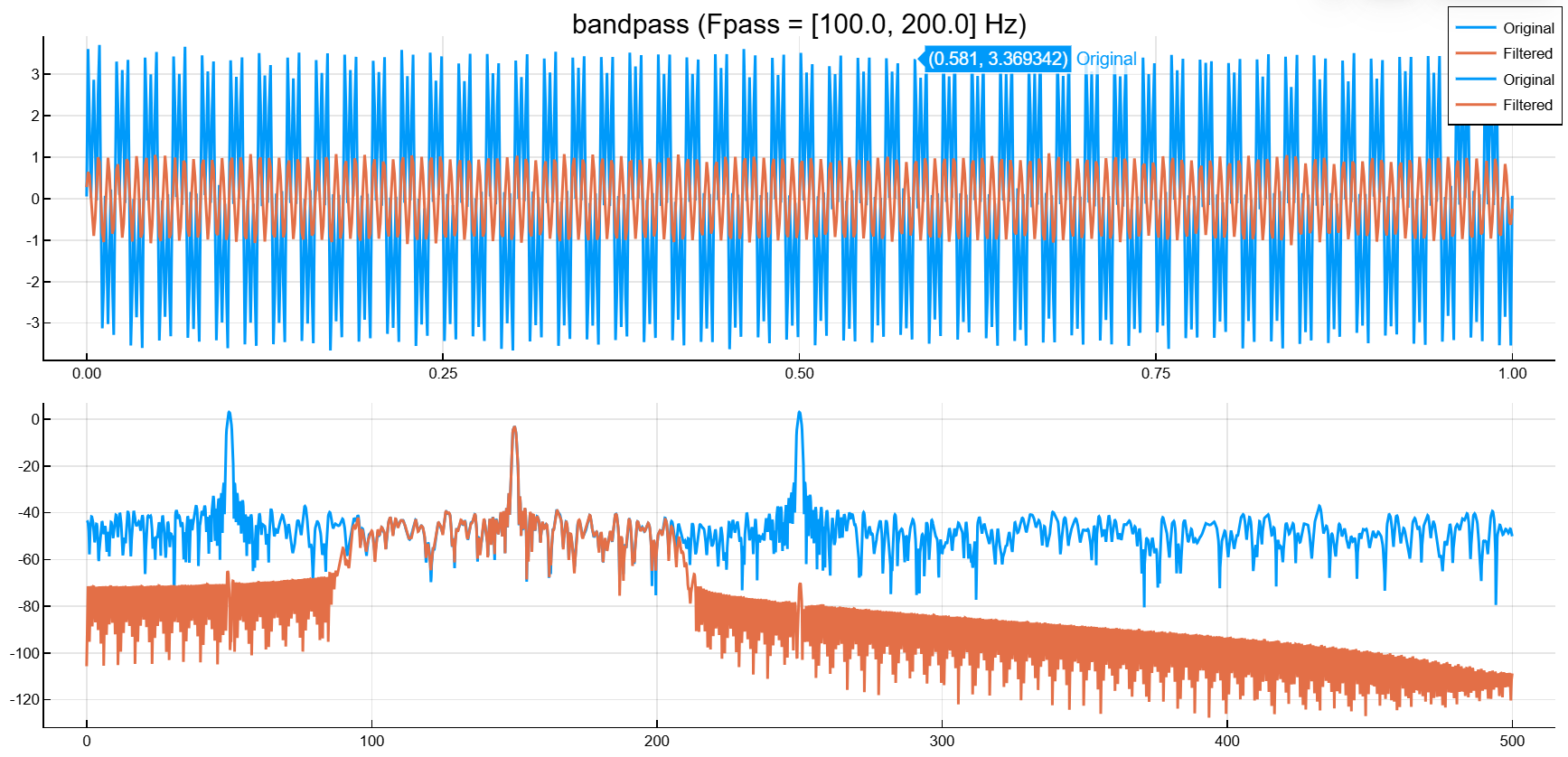

bandpass 1

Крутизна спада полосового фильтра

Details

Отфильтруем белый шум, дискретизированный с частотой 1 кГц, с помощью полосового фильтра с бесконечной импульсной характеристикой и полосой пропускания 100 Гц. Используем различные значения крутизны. Построим спектры отфильтрованных сигналов.

import EngeeDSP.Functions: randn, bandpass, pspectrum

fs = 1000;
x = randn(20000,1);

y1 = bandpass(x,[50 150],fs,"ImpulseResponse","iir","Steepness",0.5)
y2 = bandpass(x,[200 300],fs,"ImpulseResponse","iir","Steepness",0.8)
y3 = bandpass(x,[350 450],fs,"ImpulseResponse","iir","Steepness",0.95)

pspectrum([y1 y2 y3],fs,out=:plot)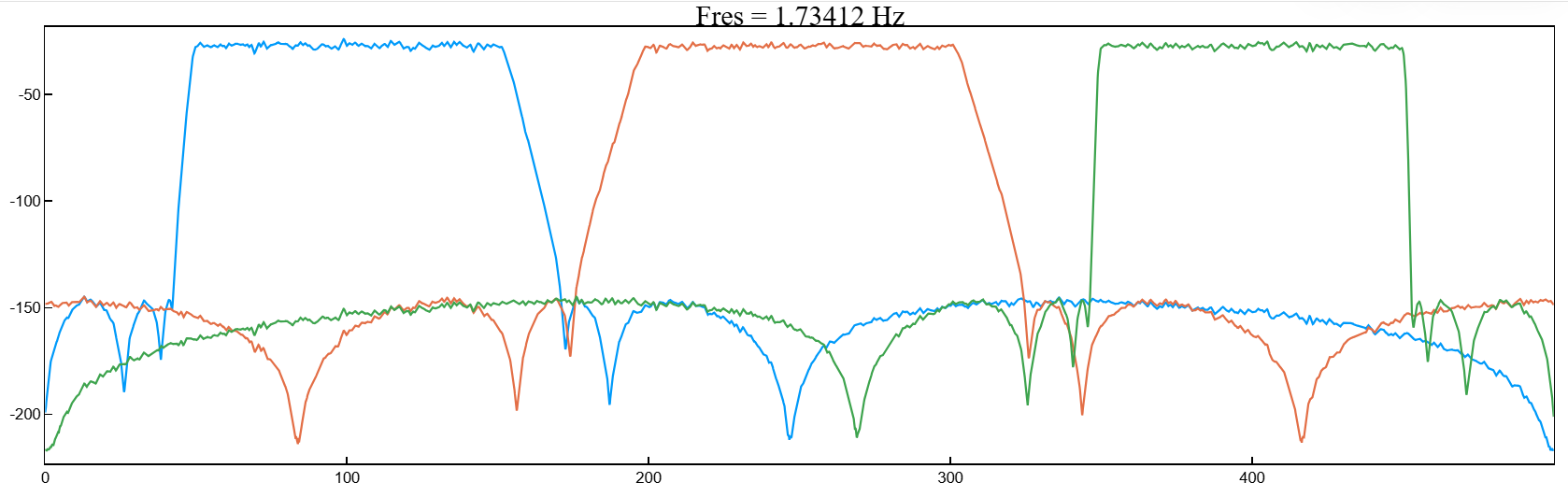

bandpass 2

Сделаем фильтры асимметричными, задав разные значения крутизны на нижних и верхних частотах полосы пропускания.

y1 = bandpass(x,[50 150],fs,"ImpulseResponse","iir","Steepness",[0.5 0.8])
y2 = bandpass(x,[200 300],fs,"ImpulseResponse","iir","Steepness",[0.5 0.8])
y3 = bandpass(x,[350 450],fs,"ImpulseResponse","iir","Steepness",[0.5 0.8])

pspectrum([y1 y2 y3],fs,out=:plot)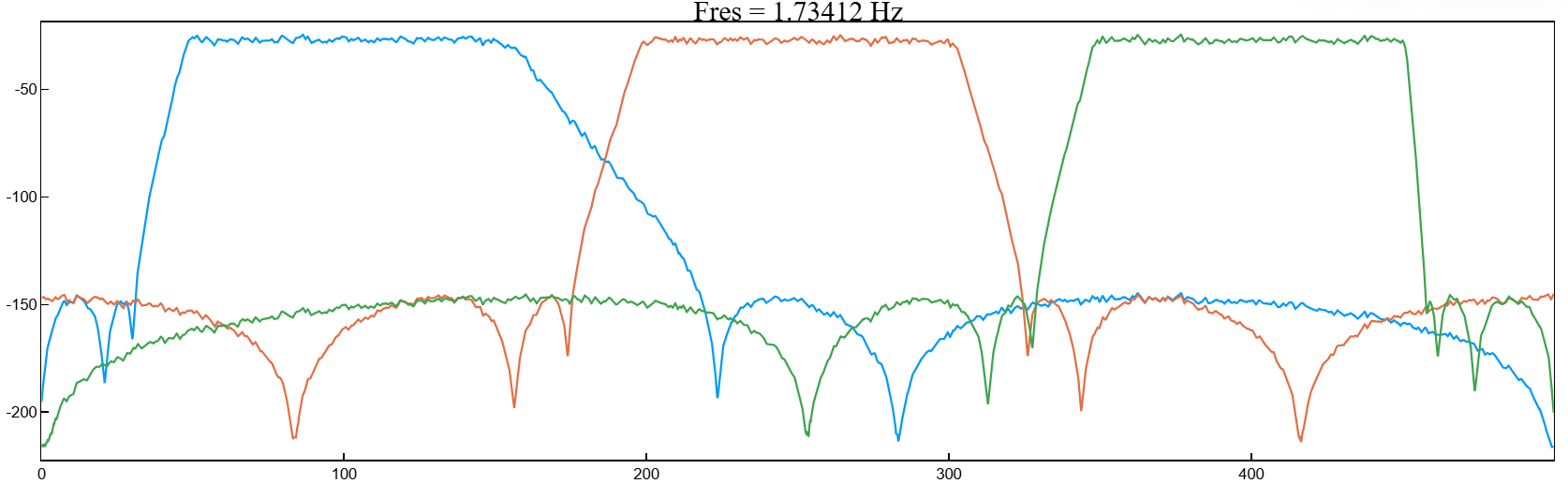

bandpass 3

Дополнительно

Крутизна спада полосового фильтра

Details

Аргумент Steepness управляет шириной переходных областей фильтра. Чем меньше крутизна, тем шире область перехода. Чем выше крутизна, тем более узкой будет область перехода.

Чтобы интерпретировать крутизну фильтра, рассмотрим следующие определения:

  • Частота Найквиста — самая высокочастотная составляющая сигнала, которая может быть дискретизирована с заданной частотой без искажений. Частота Найквиста равна рад/отсчет, если входной сигнал не содержит информации о времени, и Гц, если вы задаете частоту дискретизации.

  • Нижняя и верхняя частоты полосы задерживания фильтра и — частоты, ниже и выше которых затухание равно или больше значения, заданного с помощью StopbandAttenuation.

  • Ширина нижней переходной полосы фильтра , где — первый элемент заданных частот полосы пропускания fpass.

  • Ширина верхней переходной полосы фильтра , где — второй элемент заданных частот полосы пропускания fpass.

  • Большинство неидеальных фильтров также ослабляют входной сигнал в полосе пропускания. Максимальное значение этого частотно-зависимого ослабления называется пульсациями в полосе пропускания. Каждый фильтр, используемый в bandpass имеет пульсации в полосе пропускания 0.1 дБ.

bandpass ru

Чтобы управлять шириной переходных полос, вы можете указать Steepness как двухэлементный вектор , либо как скаляр.

Когда Steepness задан в виде вектора:

  • Функция вычисляет ширину нижней переходной полосы как

    • Когда первый элемент Steepness равен 0.5, ширина перехода составляет 50% от .

    • По мере приближения первого элемента Steepness к 1 ширина перехода постепенно уменьшается, пока не достигнет минимального значения в 1% от .

  • Функция вычисляет ширину верхней переходной полосы как

    • Когда второй элемент Steepness равен 0.5, ширина перехода составляет 50% от .

    • По мере приближения второго элемента Steepness к 1 ширина перехода постепенно уменьшается, пока не достигнет минимального значения в 1% от .

Когда Steepness задан в виде скаляра, то функция:

  • вычисляет и , используя указанное скалярное значение.

  • создает симметричный фильтр с шириной нижней и верхней переходной полосы, равной меньшему из и .

По умолчанию значение Steepness равно [0.85 0.85].