decimate

Децимация — уменьшение частоты дискретизации в целое число раз.

Библиотека

EngeeDSP

Синтаксис

Вызов функции

y = decimate(x, r, mode) — уменьшает частоту дискретизации входного сигнала x в r раз. Сигнал выходной сигнал y сокращается в r раз: length(y) = ceil(length(x)/r). Использует КИХ фильтр с конечной импульсной характеристикой, разработанный с использованием окна Хэмминга. Фильтр имеет порядок 30.

y = decimate(x, r) — функция decimate использует БИХ фильтр Чебышева I 8-го порядка.

y = decimate(x, r, n, mode) — использует КИХ фильтр, разработанный с использованием окна Хэмминга. Фильтр имеет порядок n.

y = decimate(x, r, n) — использует фильтр Чебышева порядка n.

Аргументы

Входные аргументы

# mode — использование КИХ-фильтра
строка

Details

Если установлено значение "fir", то функция decimate использует функцию fir1 для проектирования КИХ-фильтра нижних частот с частотой среза 1/r.

# x — входной сигнал
вектор

Details

Входной сигнал в виде вектора.

Типы данных

Float32, Float64

# r — коэффициент децимации
скаляр

Details

Коэффициент децимации, заданный как целое положительное число. Для получения лучших результатов при r больше 13, разделите r на меньшие множители и вызовите decimate несколько раз.

Типы данных

Float32, Float64

# n — порядок фильтрации
скаляр

Details

Порядок фильтрации, указанный как положительное целое число. Для БИХ-фильтра не рекомендуется использовать порядок фильтрации выше 13 из-за числовой нестабильности. В таких случаях функция выводит предупреждение.

Типы данных

Float32, Float64

Выходные аргументы

# y — сигнал с уменьшенной частотой дискретизации

Details

Сигнал с уменьшенной частотой дискретизации.

Типы данных

Float32, Float64

Примеры

Децимация сигнала

Details

Сгенерируем синусоидальный сигнал с частотой дискретизации 4 кГц. Уменьшим частоту дискретизации в четыре раза.

import EngeeDSP.Functions: decimate

t = 0:1/4e3:1
x = sin.(2*pi*30*t) + sin.(2*pi*60*t)
y = decimate(x, 4)

Изобразим графики исходного и сигнала с уменьшенной частотой дискретизации.

p1 = plot(0:120, x[1:121],
          seriestype = :stem,
          marker = :circle,
          markersize = 3,
          xlabel = "Sample Number",
          ylabel = "Original",
          grid = true,
          legend = false)

p2 = plot(0:30, y[1:31],
          seriestype = :stem,
          marker = :circle,
          markersize = 3,
          xlabel = "Sample Number",
          ylabel = "Decimated",
          grid = true,
          legend = false)

plot(p1, p2, layout = (2, 1))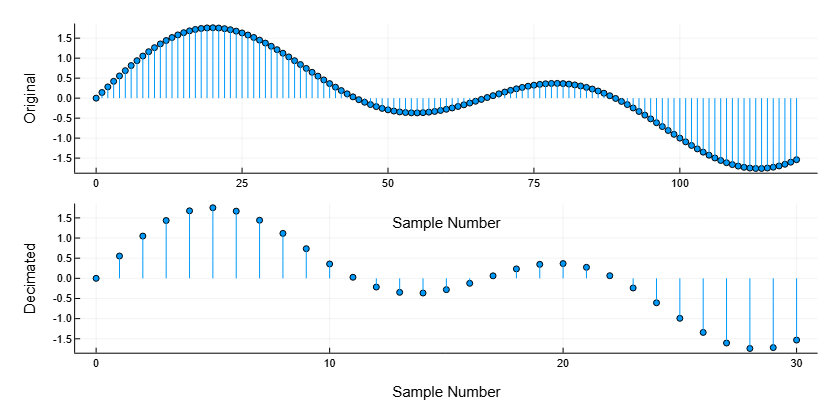

decimate 1

Децимация сигнала с использованием фильтра Чебышева

Details

Сгенерируем сигнал из двух синусоид. Уменьшим частоту дискретизации в 13 раз, используя фильтр Чебышева пятого порядка. Построим графики исходного и выходного сигналов.

import EngeeDSP.Functions: decimate

r = 13
n = 16:365
lx = length(n)
x = sin.(2*pi*n/153) + cos.(2*pi*n/127)
y = decimate(x, r, 5)

plot(0:lx-1, x,
     seriestype=:scatter,
     marker=:circle,
     label="Original",
     framestyle=:origin,
     grid = true)
plot!(lx-1:-r:0, reverse(y),
      seriestype=:scatter,
      marker=:circle,
      color=:red,
      markersize=4,
      label="Decimated",
      grid = true)

xlabel!("Sample number")
ylabel!("Signal")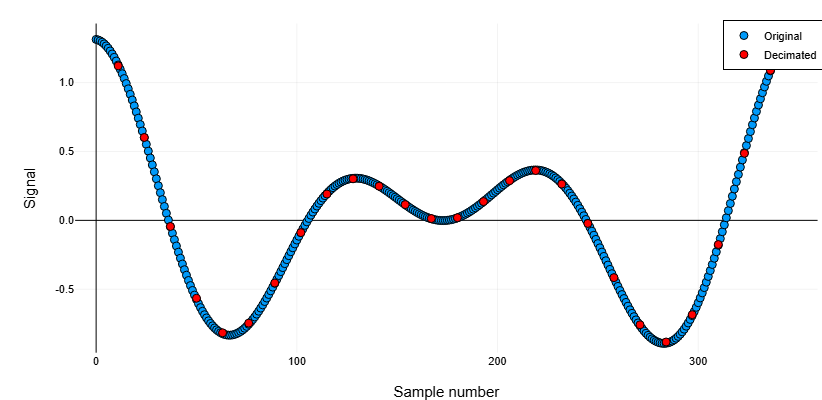

decimate 2

Децимация сигнала с использованием КИХ фильтра

Details

Сгенерируем сигнал из двух синусоид. Уменьшим частоту дискретизации в 13 раз, используя КИХ фильтр. Построим графики исходного и выходного сигналов.

import EngeeDSP.Functions: decimate

r = 13
n = 16:365
lx = length(n)
x = sin.(2*pi*n/153) + cos.(2*pi*n/127)
y = decimate(x, r, 82, "fir")

plot(0:lx-1, x,
     seriestype=:scatter,
     marker=:circle,
     label="Original",
     framestyle=:origin,
     grid=true)

plot!(0:r:lx-1, y,
      seriestype=:scatter,
      marker=:circle,
      color=:red,
      markersize=4,
      label="Decimated",
      grid=true)

xlabel!("Sample number")
ylabel!("Signal")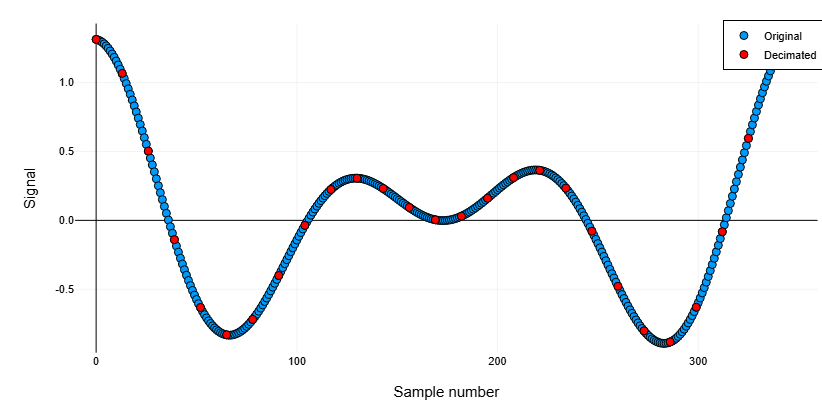

decimate 3

Алгоритмы

Децимация уменьшает первоначальную частоту дискретизации последовательности до более низкой. Это противоположность интерполяции. Функция decimate применяет к входному сигналу низкочастотную фильтрацию для защиты от наложения спектров (алиасинга) и выполняет прореживание результата. Функция использует алгоритмы прореживания 8.2 и 8.3 из [1].

decimate создает фильтр нижних частот. По умолчанию используется БИХ фильтр Чебышева I. Этот фильтр имеет нормированную частоту среза, равную 0.8/r, и пульсацию полосы пропускания, равную 0.05 дБ. Иногда указанный порядок фильтрации приводит к искажению полосы пропускания из-за ошибок округления, накопленных в результате сверток, необходимых для создания передаточной функции. Функция decimate производит автоматическое уменьшение порядка фильтрации, когда искажение приводит к тому, что амплитудная характеристика на частоте среза отличается от пульсаций более чем на 10^-6.

При выборе опции "fir" функция decimate использует функцию fir1 для проектирования КИХ-фильтра нижних частот с частотой среза 1/r.
При использовании КИХ-фильтра, функция decimate фильтрует входную последовательность только в одном направлении. Это экономит память и полезно для работы с длинными последовательностями. В случае БИХ-фильтра, функция decimate применяет фильтр в прямом и обратном направлениях, используя filtfilt для устранения фазовых искажений. По сути, этот процесс удваивает порядок фильтрации. В обоих случаях функция минимизирует переходные эффекты на обоих концах сигнала за счет согласования условий конечной точки.
И, наконец, функция decimate выполняет повторную выборку данных, выбирая все r-е точки внутри отфильтрованного сигнала. В последовательности повторной дискретизации (y), y(end) соответствует x(end) когда используется БИХ-фильтр, и y(1) соответствует x(1) при использовании КИХ-фильтра.

Литература

Digital Signal Processing Committee of the IEEE® Acoustics, Speech, and Signal Processing Society, eds. Programs for Digital Signal Processing. New York: IEEE Press, 1979.