We play the "Imperial March" on KPM RHYTHM
In this example, we will look at how to write a melody using the Engee script and then play it on KPM RHYTHM.
Introduction
In a simplified view, any melody is a sequence of sounds of varying pitch and duration, as well as their absence (pauses). Sounds can be described by harmonic signals of different pitch. The pitch of the sound, in turn, is determined by the frequency of such a signal. Summarizing, the task of writing a melody can technically be represented as the task of forming a sequence of frequencies of a single signal with different durations.
Melody preparation
The original melody is described by the notes in the image below.
For the convenience of its translation "into numbers", we will go through the following steps:
-
Determine the appropriate frequency for each note.
-
We will define the pause by the zero frequency.
-
Let's define the functions of alterations - sharp and flat, which respectively raise and lower the frequency of the note by half a tone.
-
Determine the minimum period of the signals.
-
Set the note duration functions.
-
Generate the resulting melody vector - a sequence of signal frequencies in accordance with the tempo.
Notes
Calculation of frequencies for the entire scale by evenly темперированному the musical structure is defined as follows:
where - tuning fork frequency (La of the first octave, or A4 in scientific notation),
- the number of semitones for the sound under study relative to the tuning fork for which .
Let's write down the definition of a number for notes from 5 октав. We use scientific notation to denote them.
(C2, C♯2, D2, D♯2, E2, F2, F♯2, G2, G♯2, A2, A♯2, B2) = collect(-33:-22); # Большая октава
(C3, C♯3, D3, D♯3, E3, F3, F♯3, G3, G♯3, A3, A♯3, B3) = collect(-21:-10); # Малая октава
(C4, C♯4, D4, D♯4, E4, F4, F♯4, G4, G♯4, A4, A♯4, B4) = collect(-9:2); # Первая октава
(C5, C♯5, D5, D♯5, E5, F5, F♯5, G5, G♯5, A5, A♯5, B5) = collect(3:14); # Вторая октава
(C6, C♯6, D6, D♯6, E6, F6, F♯6, G6, G♯6, A6, A♯6, B6) = collect(15:26); # Третья октава
Sound
With this definition of sound frequencies, the generated harmonic signal in the Engee model will look like this:
t = collect(0:0.0001:0.01); f = 440*2^(A4/12);
gr()
plot(t, sin.(2*pi*f*t); label="A4")
Alterations
The next stage of preparation is the definition of auxiliary functions that will simplify the rewriting of the melody. This is how you can determine the sharp (frequency increase by half a tone) and flat (frequency increase by half a tone) of a recorded note.:
# Функции альтераций
♯(n) = n + 1; # Диез
♭(n) = n - 1; # Бемоль
Pauses
If the sound of a given key is described by a certain frequency, then the pause is described by a zero frequency. To form pauses in a single sequence of numbers with the notes to determine the frequencies, we will set the pause of the shortest duration 𝄿 (the sixteenth) as a number for which the resulting frequency is . Pauses of multiple duration are determined after the sixteenth.
𝄿 = [-999]; # Шестнадцатая пауза
𝄾 = vcat(𝄿, 𝄿); # Восьмая пауза
𝄽 = vcat(𝄾, 𝄾); # Четвертная пауза
𝄼 = vcat(𝄽, 𝄽); # Половинная пауза
Minimum period
The minimum period with which the signals can change in the Engee model will depend on the minimum duration of the notes, pauses, and also on the musical tempo.
The tempo in the original musical notation is set to 𝅘𝅥=100, that is, 100 quarter durations per minute.
The minimum duration in the melody is the sixteenth. Thus, the minimum duration of the signal can be set as follows:
tempo = 60/100/4 # Шестнадцатая длительность = 150 мс
Durations
To simplify the recording of notes and their durations in the code, we define functions for different durations. All the durations except the sixteenth will be supplemented with the sixteenth duration at the end. This is a rough assumption, but it will improve the perception of the audio signal in our prototype KPM RHYTHM music player.
# Функции нотных длительностей
𝅘𝅥𝅯(n) = [n]; # Шестнадцатая
𝅘𝅥𝅮(n) = [n, 𝄿...]; # Восьмая
𝅘𝅥𝅮⋅(n) = [n, n, 𝄿...]; # Восьмая с точкой
𝅘𝅥(n) = [n, n, n, 𝄿...]; # Четвертная
𝅗𝅥(n) = [n, n, n, n, n, n, 𝄾...]; # Половинная
Melody
All the preparation has been completed, as a result, the original melody can be rewritten according to the notes as follows:
notes = vcat(𝅘𝅥(C4), 𝅘𝅥(C4), 𝅘𝅥(C4), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(E4)),
𝅘𝅥(C4), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(E4)), 𝅗𝅥(C4),
𝅘𝅥(G4), 𝅘𝅥(G4), 𝅘𝅥(G4), 𝅘𝅥𝅮⋅(♭(A4)), 𝅘𝅥𝅯(♭(E4)),
𝅘𝅥(♭(C4)), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(E4)), 𝅗𝅥(C4),
𝅘𝅥(C5), 𝅘𝅥𝅮⋅(C4), 𝅘𝅥𝅯(C4), 𝅘𝅥(C5), 𝅘𝅥𝅮⋅(B4), 𝅘𝅥𝅯(♭(B4)),
𝅘𝅥𝅯(A4), 𝅘𝅥𝅯(♯(G4)), 𝅘𝅥𝅮(A4), 𝄾, 𝅘𝅥𝅮(♯(C4)), 𝅘𝅥(♯(F4)), 𝅘𝅥𝅮⋅(F4), 𝅘𝅥𝅯(E4),
𝅘𝅥𝅯(♭(E4)), 𝅘𝅥𝅯(D4), 𝅘𝅥𝅮(♭(E4)), 𝄾, 𝅘𝅥𝅮(♭(A3)), 𝅘𝅥(♭(C4)), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(C4)),
𝅘𝅥(♭(E4)), 𝅘𝅥𝅮⋅(♭(C4)), 𝅘𝅥𝅯(♭(E4)), 𝅗𝅥(♯(G4)),
𝅘𝅥(C5), 𝅘𝅥𝅮⋅(C4), 𝅘𝅥𝅯(C4), 𝅘𝅥(C5), 𝅘𝅥𝅮⋅(B4), 𝅘𝅥𝅯(♭(B4)),
𝅘𝅥𝅯(A4), 𝅘𝅥𝅯(♯(G4)), 𝅘𝅥𝅮(A4), 𝄾, 𝅘𝅥𝅮(♯(C4)), 𝅘𝅥(♯(F4)), 𝅘𝅥𝅮⋅(F4), 𝅘𝅥𝅯(E4),
𝅘𝅥𝅯(♭(E4)), 𝅘𝅥𝅯(D4), 𝅘𝅥𝅮(♭(E4)), 𝄾, 𝅘𝅥𝅮(♭(A3)), 𝅘𝅥(♭(C4)), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(E4)),
𝅘𝅥(C4), 𝅘𝅥𝅮⋅(♭(A3)), 𝅘𝅥𝅯(♭(E4)), 𝅗𝅥(C4),
𝄼, 𝄼);
At the end of the melody, we will pause for a whole beat (𝄼, 𝄼).
println("В нашей мелодии: ", sizeof(notes), " элементов шестнадцатой длительности.\n")
# @markdown ### Результаты переноса мелодии:
println("Вот как выглядит вектор с полутонами, из которого будут сгенерированы звуковые сигналы:\n")
print(notes)
The sequence detection starts automatically when the sample model is opened. [callbacks] are used for this(https://engee.com/helpcenter/stable/ru-en/julia/JuMP/tutorials/linear/callbacks.html ) models.
The example model
The resulting sequence (melody) will be transferred to the [Repeating Sequence Stair] block (https://engee.com/helpcenter/stable/ru-en/base-lib-sources/repeating-sequence-stair.html ) - it will transfer values from the vector to the output one by one with a given period. Using the blocks of the Engee standard library, we will then convert these values into a sinusoidal signal of a given frequency. The received signals will be transmitted to the KPM RHYTHM analog output unit, the [RITMeX GP-LC-4X] module (https://engee.com/helpcenter/stable/ru-en/ritmex-gp-lc-45/blocks.html ) and in the graph output block on the monitor.
KPM RHYTHM simulation allows you to reproduce the model in real time. This is necessary, for example, to accurately control the frequency and duration of the generated signal.
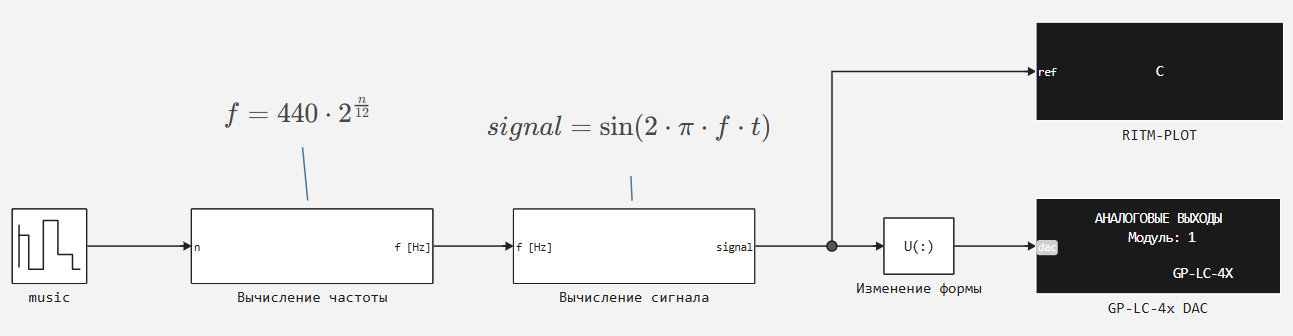
Model Settings:
-
The size of the modeling step, with -
1e-5 -
Simulation mode -
Быстрый счёт -
End of simulation -
Inf -
Action in case of overflow of the calculation step -
Уведомить
Hardware: Audio output to speaker
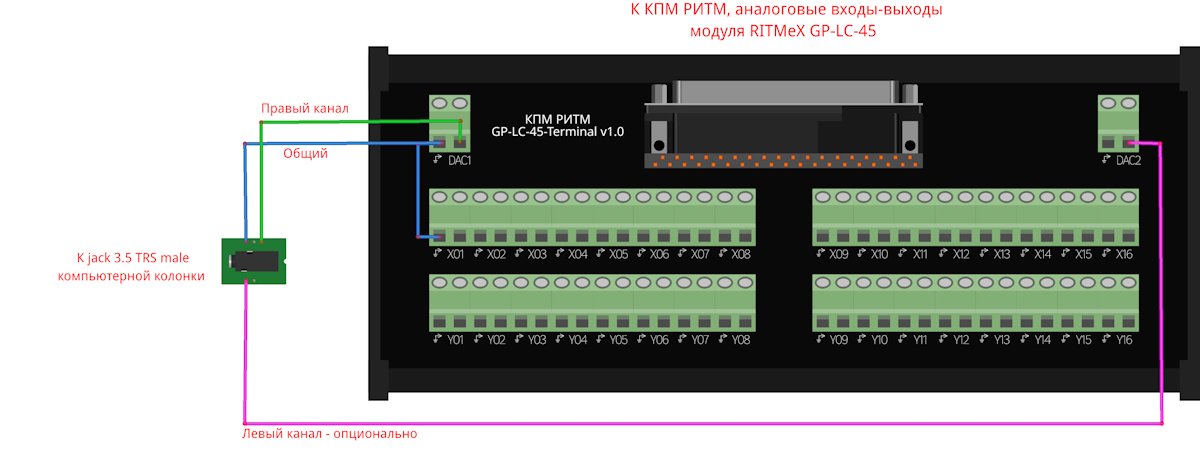
For audio output, we use computer speakers with a 3.5 mm jack TRS analog signal input. The example uses a single audio channel (mono audio). For stereo sound on the GP-LC module, it is sufficient to realize the signal output from the second channel of the DAC2 DAC. The connection of the speakers to the RHYTHM module is shown in the figure below.:
Rhythm-based modeling
Before starting the simulation on a real-time machine, it is necessary to establish a connection and several preparatory steps, which are described in the corresponding work example.
After starting the model on the rhythm, an analog signal with different duration and frequency can be observed on the monitor, and a digitized melody will be heard in the right speaker. Without connecting to the rhythm, you can listen to it in the output of the code cell below:
import Pkg; Pkg.add(["WAV","Base64"])
using WAV, Base64
using WAV, Base64
x, fs = wavread( "$(@__DIR__)/the imperial march.wav" );
buf = IOBuffer();
wavwrite(x, buf; Fs=fs);
data = base64encode(unsafe_string(pointer(buf.data), buf.size));
markup = """<audio controls="controls" {autoplay}>
<source src="data:audio/wav;base64,$data" type="audio/wav" />
Your browser does not support the audio element.
</audio>"""
display( "text/html", markup );
You can run the simulation on the rhythm directly from the script - for this we use the external hardware support package and the corresponding software management methods.
A detailed description of the automated real-time testing process was given in previous примерах.
engee.package.install("Engee-Device-Manager");
# @markdown ## Подключение КПМ РИТМ
IP = "192.168.56.3" # @param {type:"string",placeholder:"192.168.56.3"}
порт = "8000" # @param {type:"string",placeholder:"8000"}
using Main.EngeeDeviceManager.Targets
using Main.EngeeDeviceManager.Targets.RITM_API
ritm = Targets.RITM.Ritm()
Targets.RITM_API.setUrl(ritm, "http://$IP:$порт/")
println("КПМ РИТМ подключен: ", RITM_API.isConnected(ritm))
# @markdown ## Запуск модели в режиме Standalone
имя_модели = "the_imperial_march" # @param {type:"string",placeholder:"hil_dcm"}
path = joinpath(@__DIR__, "$имя_модели.engee")
model = engee.load(path)
resp = Targets.upload_model(ritm, model)
println("\n", "Загрузка модели: ", resp)
resp = Targets.generate_executable_code(ritm, model, false)
println("\n", "Генерация кода: ", resp)
resp = Targets.compile_model(ritm, model)
println("\n", "Компиляция: ", resp)
Targets.start_model(ritm, model)
engee.close(model; force=true)
Conclusion
In this example, we examined not only the mathematical foundations of music and the synthesis of musical notation signals, but also reproduced a simple melody using a real-time stand. This is just a small example from the field of digital synthesis of audio signals that can be implemented in Engee and on KPM RHYTHM.