Engee documentation

Memory Node

Page in progress.

See also:
First steps in finite automata
The logic of finite automata operation
Hierarchy of the state machine

History Junction stateflow history junction — this is an element the state machine Engee, which captures the state of the children states stateflow state inside the parent state, so that when reactivated, it returns to the last active state.

Read more about parent and child states in the article Hierarchy of the state machine.

History Junction it can only be located inside states. Incorrect location will give an error.:

stateflow history junction 1 en

History Junction records the activity of child states inside the parent state. When the parent state becomes active for the first time, the state machine uses default transition stateflow default transition 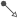to determine which child state becomes active. However, if the parent state becomes inactive and is then reactivated, the memory node allows you to return to the last active child state, bypassing the default transition.

For example, there is an automatic door, which can have only two child states — open and Closed. The parent state will be the "Door_Activity" state, which is common to the child states. We obtain the following model of a finite automaton:

stateflow history junction 2

  1. When the state machine first switches to the Door_Activity state, the Closed state is activated by default;

  2. If the door opens, and then the system temporarily shuts down (switching to the "inactive" state, i.e. the parent state of Door_Activity will cease to be active), the memory node remembers the Open state.;

  3. When the Door_Activity state is reactivated, the door automatically returns to the Open state, rather than Closed, as it would be without the memory node.

History Junction as an internal transition

History Junction It can be used as an internal passage.

An internal transition is a mechanism in the hierarchy of states of a finite automaton that allows you to move from the current state to one of its child states without going to a higher level. This transition is performed automatically when the parent state is activated and can be either unconditional or dependent on certain conditions.

An internal transition is created from the frame of the parent state to the child state, but in our case it will go to the memory node.:

internal transition sm

This transition works as a self-loop for each child state. When the internal transition condition is met, the state machine temporarily exits the active child state, and then immediately returns to it. This allows you to reactivate the state by performing all related actions (for example, groups of operators during and on). Therefore, the memory node, as an internal transition, helps manage transitions while maintaining the current state of the system.

Let’s look at how the internal transition to the memory node works. To do this, let’s imagine the following model with the parent state A and two child states — A1 and A2. The model will not have a memory node and conditions on the internal transition:

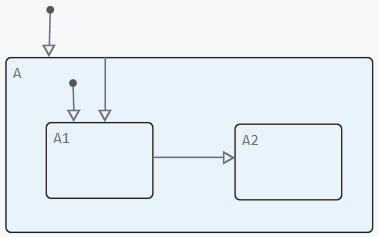
internal transition sm 1

The internal transition from state A to A1 is performed unconditionally, that is, every time the state A is activated. This makes the A2 state unreachable without using a memory node. Such a model of a finite state machine will work according to the following logic:

Logics of a finite state machine in a model without a memory node and conditions

  1. Activating the Chart block, starting the operation of the model’s state machine:

    1. 1. Transition to the A state;

    1. 2. Activation of the A state;

    1. 3. Transition to the A1 state;

    1. 4. Activation of the A1 state;

    1. 5. Chart and the states A, A1 fall asleep.

  2. Chart and the active state A are waking up:

    1. 1. The groups of operators during and on are executed (if any);

    1. 2. Deactivating the A1 state;

    1. 3. Activation of the A1 state;

    1. 4. The Chart block and the states A, A1 fall asleep.

  3. Return to step 2, repeat the cycle.

Now let’s add a condition (temporal logic operator every) on an internal transition:

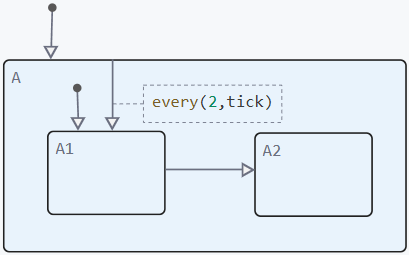
internal transition sm 2

After adding the condition, the transition from state A to A1 will be performed only every second time the state A is awakened. For odd awakenings, the transition A1 → A2 occurs, and for even ones, the transition A2 → A1 occurs. Therefore, the model will work according to the following logic:

Logics of a finite state machine in a model without a memory node with the condition

  1. Activating the Chart block, starting the operation of the model’s state machine:

    1. 1. Transition to the A state;

    1. 2. Activation of the A state;

    1. 3. Transition to the A1 state;

    1. 4. Activation of the A1 state;

    1. 5. Chart and the states A, A1 fall asleep.

  2. The Chart block and the active state A are waking up (waking up #1, 3, 5…​ states A):

    1. 1. Transition A1→A2 is in progress;

    1. 2. Deactivating the A1 state;

    1. 3. Activation of the A2 state;

    1. 4. The Chart block and the states A, A2 fall asleep.

  3. The Chart block and the active state A are waking up (waking up #2, 4, 6…​ states A):

    1. 1. The during and on operator groups are executed (if any);

    1. 2. The internal transition condition is triggered (the awakening is even), and it is fulfilled;

    1. 3. Deactivating the A2 state;

    1. 4. Activation of the A1 state;

    1. 5. Chart and the states A, A1 fall asleep.

  4. Return to step 2, repeat the cycle.

Now let’s consider a model with a memory node on the inner junction. Additionally, we add a temporal logic operator. after and another external state, as shown in the figure:

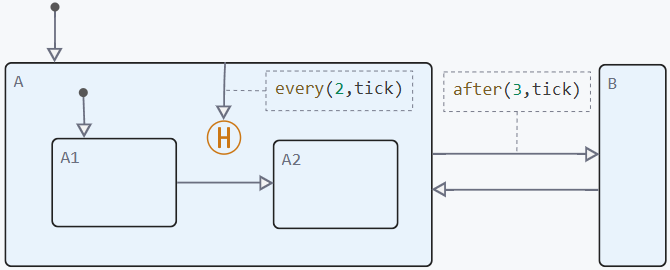
internal transition sm 3

Recall that the task of the memory node on the internal transition is to remember the last active child state and return to it when the conditions are met. Then the model will work according to the following logic:

Logic of a finite state machine in a model with a memory node and a condition_

  1. Activating the Chart block, starting the operation of the model’s state machine:

    1. 1. Transition to the A state;

    1. 2. Activation of the A state;

    1. 3. Transition to the A1 state;

    1. 4. Activation of the A1 state;

    1. 5. Chart and the states A, A1 fall asleep.

  2. Chart and the active state A wake up (the first awakening of the state A):

    1. 1. Transition A1→A2 is in progress;

    1. 2. Deactivating the A1 state;

    1. 3. Activation of the A2 state;

    1. 4. History Junction remembers the status of A2;

    1. 5. Chart and the states A, A2 fall asleep.

  3. Chart and active state A wake up (second waking of state A):

    1. 1. The groups of operators during and on are executed (if any);

    1. 2. The condition of internal transition to the memory node is triggered, and it is executed in the stored state A2;

    1. 3. Deactivating the A2 state;

    1. 4. Activation of the A2 status;

    1. 5. History Junction remembers the status of A2;

    1. 6. Chart and the states A, A2 fall asleep.

  4. Chart wakes up (third awakening of state A):

    1. 1. The transition condition A→B is triggered, and it is executed;

    1. 2. Deactivating the A2 state;

    1. 3. Deactivating the A state;

    1. 4. Activation of the B state;

    1. 5. Chart and B state fall asleep.

  5. Chart wakes up:

    1. 1. An unconditional transition is performed B→A;

    1. 2. Activation of the A state;

    1. 3. Activation of the stored state A2;

    1. 4. History Junction remembers the status of A2;

    1. 5. Chart and the states A, A2 fall asleep.

  6. Chart, A and A2 wake up (first wake-up A):

    1. 1. History Junction remembers the status of A2;

    1. 2. Chart, A and A2 fall asleep.

  7. Return to step 3, repeat the cycle.

Thus, an internal transition to a memory node allows you to temporarily exit the current child state and return to it if the transition condition is met. This happens immediately after executing the during and on groups of statements in the parent state. History Junction remembers the last active child state, helping in transition management.

The main differences between a memory node with an internal transition and without it are as follows:

  • History Junction without internal transition simply remembers the last active state and restores it when re-entering the parent state.

  • History Junction with internal transition activates the stored state only when the transition condition is met, and this happens immediately after executing the during and on operator groups of the parent state.

  • History Junction without internal transition works passively — it restores the state only when the parent state is reactivated.

  • History Junction with internal transition active — it allows you to temporarily exit the current state and return to the remembered one if the transition condition is true.

  • History Junction without an internal transition can be placed anywhere in the state (including child states), and it will work regardless of transitions.

  • History Junction with an internal transition is linked to a specific transition and is activated only when it is completed.

  1. Chart

  2. State Machines

  3. Transition

  4. Condition