First steps in finite automata
| This example demonstrates finite state machine logic and is not exhaustive. For a deeper understanding of finite automata, refer to other articles in the section State Machines. |
Consider working with a finite automaton (SPACECRAFT) using the example of an automatic fire extinguishing system model. The final model will include the main elements of the KA library  :
:
For ease of understanding
Memory Node  will not be used. will not be used.
|
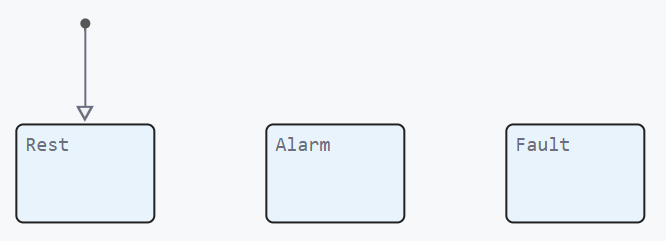
Let’s assume that the model can be in the following states:
-
Rest (rest) — the maximum smoke concentration is not exceeded;
-
Alarm (alarm) — the system turns on the sprinkler;
-
Fault (malfunction) — self-diagnosis showed a malfunction of the system, further work is impossible.
The system has one input — the concentration of smoke in the air and two outputs — "sprinklers" and "malfunction lamp". Depending on the value of the input signal, the system enters one of the possible states, and the values of the output signals are set accordingly:
-
Rest (rest) — the sprinklers are off, the fault lamp is off;
-
Alarm (alarm) — sprinklers are on, the fault lamp is on;
-
Fault (malfunction) — the sprinklers are turned off, the malfunction lamp is on.
The system moves from one state to another by transitions:
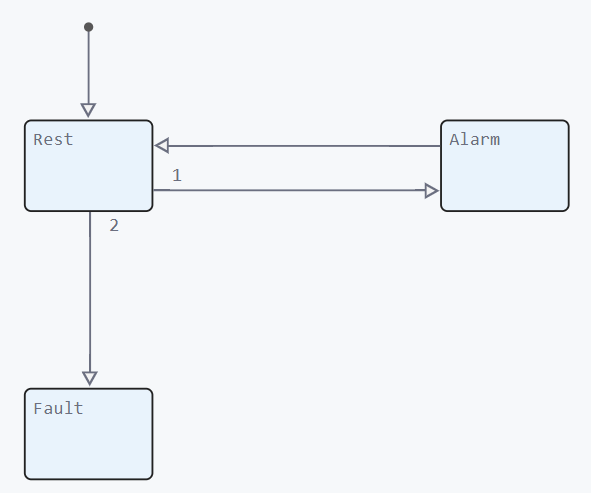
Transitions between states occur when certain conditions are met ([]), set in the model. The transition condition can be an event, a logical condition, or a time. In our example, the condition for the transition from the state of Rest to the state of Alarm will be exceeding the maximum permissible smoke concentration, and Malfunction occurs if the sensor shows a negative concentration value.
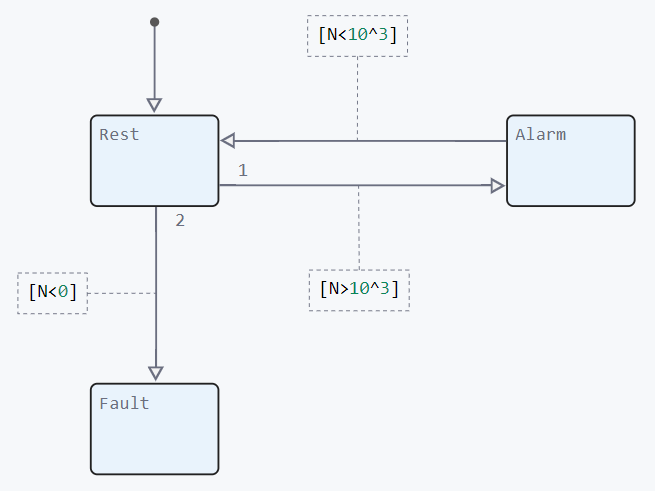
To add more complex conditions to the model, you can use nodes:
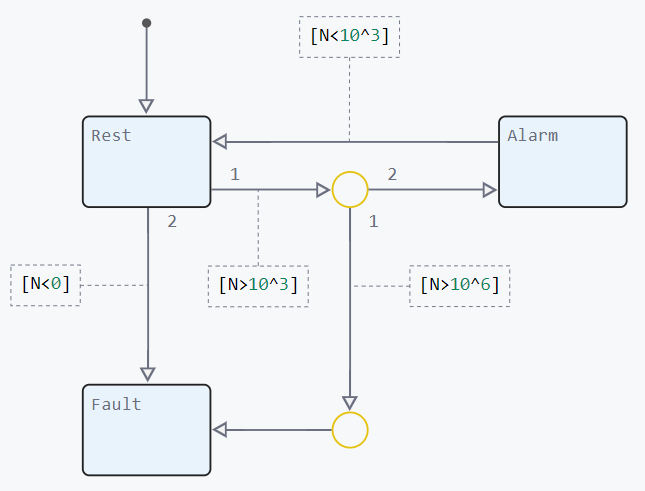
The upper node blocks the transition from the Rest state to the Alarm state if the concentration is too high, as this does not correspond to the real situation. Instead, the system also enters the Fault state.
An example of a model of an automatic fire extinguishing system illustrates the basic principles of operation of a finite automaton: separation of logic into states, determination of conditions for transitions, and usage of nodes to process more complex scenarios. This approach allows us to develop a reliable and predictable system that responds correctly to changes in input signals, minimizing errors when it is implemented in the real world.


