Battery

Battery Model.

blockType: AcausalElectricPowerSystems.Sources.Battery

Path in the library:

/Physical Modeling/Electrical/Sources/Battery

Description

The Battery block is a simple battery model. You can also expose the charge output port and the thermal port of the battery.

To measure the internal battery charge level, under Main select the checkbox for the Expose charge measurement port parameters. This action displays an additional q port that outputs the current battery charge value. Use this functionality to change the load behaviour depending on the state of charge without the complexity of building a charge level meter.

To model the thermal effects of the battery, in the Thermal Port section, select the checkbox for the Thermal port parameters. This action opens an additional H thermal port. If this mode is selected, additional parameters must be entered, in particular a second temperature must be set. For more information, see the Thermal Effects Modelling section.

The equivalent battery circuit consists of the fundamental battery model, self-discharge resistance , charge dynamics model and series resistance .

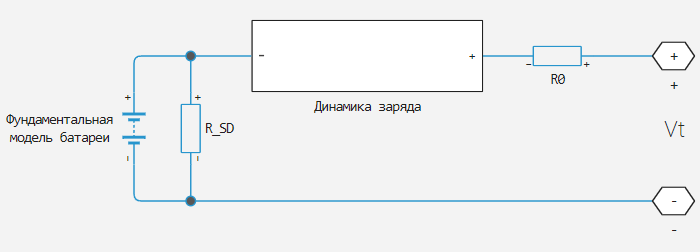
battery scheme 1

Battery model

If `Infinite' is selected for the Battery charge capacity parameters, the unit models the battery as a series resistor and constant voltage source. The charge level does not change over time.

If Finite is selected for the Battery charge capacity parameters, the block models the battery as a series resistor and a charge-dependent voltage source. In this case, the voltage is a function of charge and has the following dependence:

where:

SOC (state of charge) is the ratio of the current charge to the nominal capacity of the battery.
- is the voltage when the battery is fully charged with no load (nominal voltage). It is set by the Nominal voltage parameters.
β is a coefficient that is calculated so that the battery voltage is V1 when the battery is charged AH1. Set the V1 voltage and AH1 cell capacity using the block parameters. AH1 is the charge when the idle (open circuit) voltage is equal to V1 and V1 is less than the nominal voltage.

The equation defines an approximation of the relationship between voltage and remaining charge. This approximation reproduces the increasing rate of voltage drop at low values of charge and ensures that the battery voltage becomes zero when the charge level is zero. The advantage of this model is that it requires few parameters that are readily available in most data sheets.

Modelling battery extinction

For battery models with a finite charge capacity, it is possible to model the degradation of battery performance as a function of the number of discharge cycles. This degradation is called battery extinction. To use it, select the checkbox for the Battery fade parameters. This setting opens additional parameters in the Fade section.

The block implements battery fade by scaling certain battery parameters values that you specify in the Main section based on the number of completed discharge cycles. The block uses multipliers , and for the Cell capacity (Ah rating), Internal resistance and Voltage V1 when charge is AH1 parameters, respectively. These multipliers in turn depend on the number of discharge cycles:

Where:

- is a multiplier for the rated capacity of the battery.
- multiplier for the series resistance of the battery.
- multiplier for voltage V1.
- number of discharge cycles performed.
- number of complete discharge cycles completed before the start of the simulation.
- the nominal capacity of the battery in ampere hours.
- the instantaneous output current of the battery.
- Heaviside ("step") function for the instantaneous battery output current. This function returns 0 if the argument is negative and 1 if the argument is positive.

The block calculates the coefficients k₁, k₂, and k₃ by substituting the parameters values specified in Fade into these battery equations. For example, the block’s parameter set by default corresponds to the following coefficient values:

You can also define a starting point for modelling based on previous charge-discharge history using the high-priority variable Discharge cycles.

Modelling thermal effects

If the Thermal port parameter is checked, you must set additional parameters at the second temperature to determine the behaviour of the battery. The extended equations for the voltage when you set the thermal port are as follows:

Where:

- is the temperature of the battery.
- is the nominal temperature of the measurement.
- temperature dependence coefficient of parameters for .
.
- coefficient of temperature dependence of the parameters for β.
- is calculated in the same way as described in Battery Model, usage of the temperature modified nominal voltage .

Internal series resistance, self-discharge resistance, and any charge-dynamic resistances are also functions of temperature:

where is the coefficient of temperature dependence of the parameters.

All temperature dependence coefficients are determined from the respective values you enter for the nominal and second measurement temperature. If charge dynamics is included in the model, the time constants vary with temperature in a similar way.

The battery temperature is determined by summing all ohmic losses included in the model:

where:

- is the thermal mass of the battery.
- corresponds to the _i_th ohmic loss member. Depending on the configuration of the unit, the losses can be as follows:
- Series resistance
- Self-discharge resistance
- First segment of charge dynamics
- Second segment of charge dynamics
- Third segment of charge dynamics
- Fourth segment of charge dynamics
- Fifth segment of charge dynamics
- voltage drop on the i-th resistance.
- is the _i_th resistance.

Charge dynamics modelling

You can simulate the battery charge dynamics using the Charge dynamics parameters:

No dynamics - the equivalent circuit contains no parallel RC sections. There is no delay between the contact voltage and the internal battery charge voltage.
One time-constant dynamics - the equivalent circuit contains one parallel RC section. Specify the time constant using the First time constant parameters.
Two time-constant dynamics - the equivalent circuit contains two parallel RC sections. Specify the time constants using the First time constant and Second time constant parameters.
Three time-constant dynamics - the equivalent circuit contains three parallel RC sections. Set the time constants using the parameters First time constant, Second time constant and Third time constant.
Four time-constant dynamics - the equivalent circuit contains four parallel RC sections. Set the time constants using the parameters First time constant, Second time constant, Third time constant and Fourth time constant.
Five time-constant dynamics - the equivalent circuit contains five parallel RC sections. Specify the time constants using the parameters First time constant, Second time constant, Third time constant, Fourth time constant and Fifth time constant.

This figure shows the equivalent circuit for a unit configured with two time constant speakers.

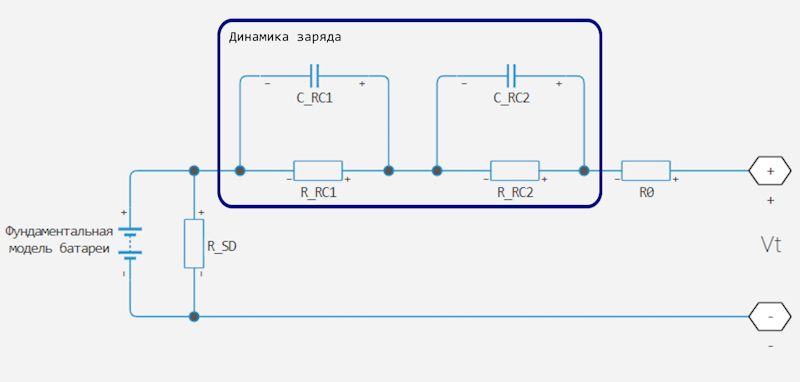
battery scheme 2

In the schematic:

and are parallel RC resistors. Set these values using the First polarisation resistance and Second polarisation resistance parameters respectively.
and are parallel RC capacitances. The time constant τ for each parallel section relates the values of R and C using the relationship . Set the τ for each section using the parameters First time constant and Second time constant respectively.
- series resistance. Set this value using the Internal resistance parameters.

Modelling battery ageing

For battery models with a finite charge capacity, it is possible to simulate the deterioration that occurs when the battery is not in use. To do this, the Calendar aging parameters must be checked. Calendar aging affects both internal resistance and capacity. In particular, the increase in resistance depends on various mechanisms such as solid electrolyte interface (SEI) formation at the anode and cathode and current collector corrosion. These processes are mainly dependent on storage temperature, state of charge and time.

The Battery block applies calendar aging only during initialisation. When you check the Calendar aging parameter, a Vector of time intervals parameter appears in the block settings that stores the time intervals when the battery aged before the simulation started. Calendar aging during simulation is not covered by this parameter.

This equation determines the increase in battery contact resistance as a result of calendar aging:

Where:

- Open-circuit voltage normalised to the nominal value. Parameters Normalised open-circuit voltage during storage, V/Vnom.
- Internal resistance. Parameters Internal resistance.
- time sample obtained from the Vector of time intervals parameters.
- A sample of temperatures obtained from the Vector of temperatures parameters.
- number of elements of the temperature sample.
b - linear scaling for voltage. Parameters Linear scaling for voltage, b.
c - constant offset for voltage. Parameters Constant offset for voltage, c.
d - temperature-dependent exponential increase. Parameters Temperature-dependent exponential increase, d.
a - time exponent. Parameters Time exponent, a.
q - electron charge, kl.
k - Boltzmann constant, J/K.

The R_age_multiplier variable in the Data Inspector stores data on the calendar aging of the battery in the contacts with increasing resistance:

For block thermal modelling options, if you set the Storage condition parameter to Fixed open-circuit voltage, you must specify the optional Open-circuit voltage measurement temperature parameter to convert the open-circuit storage voltage to a temperature-independent charge state during storage:

The open-circuit voltage as a function of storage temperature is determined by this equation:

Finally, this equation defines the increase in resistance of the battery terminals due to calendar aging as a function of storage temperature:

Assumptions and limitations

The self-discharge resistance is assumed to be independent of the number of discharge cycles.
For the battery thermal modelling option, you provide attenuation data only for operation at the reference temperature. The block applies the same multipliers , and to the parameters values corresponding to the second temperature.
When using the thermal block modelling options, use caution when operating at temperatures outside the temperature range limited by the Measurement temperature and Second measurement temperature parameters. The unit uses linear interpolation for the coefficients of the derivative equations, and simulation results may become unphysical outside this range.

Ports

Output

SOC - battery level
scalar

Charge Level. Use this output port to change the load behaviour depending on the charge level without the complexity of building a charge value meter.

The level of charge is a normalised value equal to the ratio of the current charge to the nominal battery capacity . The unit estimates the current charge of the battery by integrating the output current of the battery terminals. To convert the state of charge to actual charge, you must use the correct rated battery capacity for each temperature.

Dependencies

To use this port, select the check box for the Expose charge measurement port parameter and set the Measurement output type parameter to SOC.

q - current battery charge, Kl
scalar

Internal charge in coulombs. Use this output port to change the load behaviour as a function of charge, without resorting to the complexities of building a charge magnitude meter.

Dependencies

To use this port, check the Expose charge measurement port parameter and set the Measurement output type parameter to `Charge in Coulombs'.

Non-directional

+ - positive contact
electricity

The electrical port associated with the positive contact of the battery.

- - negative contact
electricity

Electrical port associated with the negative contact of the battery.

H - battery heat port
heat

Thermal port connected to the battery thermal mass. When this port is activated, specify additional parameters to define the behaviour of the battery. For more information, refer to Modelling thermal effects.

Dependencies

To use this port, under Thermal Port, select the checkbox for the Thermal port parameters.

Parameters

Main

Nominal voltage, Vnom - nominal output voltage of a fully charged battery
12 V (By default) | positive number

The idle voltage of a fully charged battery.

Current directionality - current direction influence
Off (By default) | On

If this checkbox is selected, the internal resistance will depend on the current direction.

Internal resistance - internal resistance of the battery
2 ohms (by default) | positive number.

Resistance of internal battery connections.

Dependencies

To use this parameter, uncheck the Current directionality parameters.

Internal resistance during charging - internal resistance of the battery during charging
2 ohms (by default) | positive number.

The internal resistance of the battery during the charging phase.

Dependencies

To use this parameter, check the Current directionality parameters.

Internal resistance during discharging - internal resistance of the battery during discharging
2 ohms (by default) | positive number.

The internal resistance of the battery during the discharging phase.

Dependencies

To use this parameter, check the Current directionality parameters.

Battery charge capacity - selects the battery model
Infinite (By default) | Finite.

Select one of the battery charge capacity modelling options:

Infinite - battery voltage is independent of the charge received from the battery, infinite capacity.
Finite - battery voltage decreases as the charge decreases.

Cell capacity (Ah rating) - rated capacity of the battery at full charge
50 A*h (By default) | Positive number

The maximum (nominal) battery charge in ampere hours. To set a target value for the initial battery charge at the start of the simulation, use the high-priority variable Charge.

Dependencies

To use this parameter, set the Battery charge capacity parameters to Finite.

Voltage V1 when charge is AH1 - output voltage at charge level AH1
11.5 V (by default) | positive number.

The main battery output voltage at AH1 charge level as specified in the parameter Charge AH1 when no-load voltage is V1. This parameter must be less than Nominal voltage, Vnom.

Dependencies

To use this parameter, set the Battery charge capacity parameters to Finite.

Charge AH1 when no-load voltage is V1 - charge level when no-load output voltage is V1
25 A*h (by default) | positive number

The battery charge level corresponding to the idle output voltage and set by the parameters Voltage V1 when charge is AH1.

Dependencies

To use this parameter, set the Battery charge capacity parameters to Finite.

Self-discharge - select whether to simulate battery self-discharge.
Disabled (By default) | On

If the checkbox is selected, the unit simulates battery self-discharge. The block simulates this effect as a resistor connected to the terminals of the fundamental battery model.

As the temperature increases, the self-discharge resistance decreases, resulting in an increase in self-discharge. If the resistance decreases too quickly, thermal discharge of the battery and numerical instability can occur. You can solve this problem by doing one of the following:

Reduce the thermal resistance.
Decrease the gradient of self-discharge resistance as a function of temperature.
Increase the self-discharge resistance.

Dependencies

To use this parameter, set the Battery charge capacity parameters to Finite.

Self-discharge resistance is the resistance reflecting the self-discharge of the battery
2000 ohms (by default) | positive number.

The resistance in the fundamental battery model that reflects the self-discharge of the battery.

Dependencies

To use this parameter, select the Self-discharge checkbox for the Self-discharge parameters.

Measurement temperature - the temperature at which the parameters of the unit are measured
298.15 K (by default) | positive number.

The T₁ temperature at which the unit parameters are measured in Main. For more information, see Modelling thermal effects.

Dependencies

To use this parameter, select the checkbox for the Thermal Port parameters.

Expose charge measurement port - whether or not to open the charge measurement port
Off (By default) | On

Select the checkbox to open the charge measurement port and measure the internal battery charge level.

Measurement output type - select the signal in the measurement port
Charge in Coulombs (By default) | SOC

The parameters has two values:

SOC - the output receives SOC charge level values.
Charge in Coulombs - the output receives values of charge q in Coulombs.

Dependencies

This parameter is used if the Expose measurement port parameter is set to on.

Dynamics

Select how the battery charge dynamics are modelled. This parameter determines the number of parallel RC sections in the equivalent circuit:

No dynamics - the equivalent circuit contains no parallel RC sections. There is no delay between the contact voltage and the internal battery charge voltage.
One time-constant dynamics - the equivalent circuit contains one parallel RC section. Specify the time constant using the First time constant parameters.
Two time-constant dynamics - the equivalent circuit contains two parallel RC sections. Specify the time constants using the First time constant and Second time constant parameters.
Three time-constant dynamics - the equivalent circuit contains three parallel RC sections. Set the time constants using the parameters First time constant, Second time constant and Third time constant.
Four time-constant dynamics - the equivalent circuit contains four parallel RC sections. Set the time constants using the parameters First time constant, Second time constant, Third time constant and Fourth time constant.
Five time-constant dynamics - the equivalent circuit contains five parallel RC sections. Specify the time constants using the parameters First time constant, Second time constant, Third time constant, Fourth time constant and Fifth time constant.

First polarisation resistance is the first RC resistance.
0.005 ohms (by default) | positive number.

The resistance of the first parallel RC section. This parameter primarily affects the ohmic losses of the RC section.

Dependencies

To use this parameter, set the Charge dynamics parameter to One time-constant dynamics, Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics or Five time-constant dynamics.

First time constant is the first RC time constant
30 s (by default) | `positive number

The time constant of the first parallel RC section. This value is equal to R*C and affects the dynamics of the RC section.

Dependencies

Second polarisation resistance - second RC resistance
0.005 ohms (by default) | positive number.

The resistance of the second parallel RC section. This parameter primarily affects the ohmic losses of the RC section.

Dependencies

To use this parameter, set the Charge dynamics parameters to Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics or Five time-constant dynamics.

Second time constant - second RC time constant
30 s (by default) | positive number

The time constant of the second parallel RC section. This value is equal to R*C and affects the dynamics of the RC section.

Dependencies

To use this parameter, set the Charge dynamics parameters to Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics or Five time-constant dynamics.

Third polarisation resistance is the third RC resistance
0.005 ohms (by default) | positive number.

Resistance of the third parallel RC section. This parameter primarily affects the ohmic losses of the RC section.

Dependencies

To use this parameter, set the Charge dynamics parameters to Three time-constant dynamics, Four time-constant dynamics or Five time-constant dynamics.

Third time constant is the third RC time constant
30 s (by default) | `positive number

The time constant of the third parallel RC section. This value is equal to R*C and affects the dynamics of the RC section.

Dependencies

To use this parameter, set the Charge dynamics parameters to Three time-constant dynamics, Four time-constant dynamics or Five time-constant dynamics.

Fourth polarisation resistance is the fourth RC resistance
0.005 ohms (by default) | positive number.

The resistance of the fourth parallel RC section. This parameter primarily affects the ohmic losses of the RC section.

Dependencies

To use this parameter, set the Charge dynamics parameters to Four time-constant dynamics or Five time-constant dynamics.

Fourth time constant - Fourth RC time constant
30 s (by default) | positive number.

The time constant of the fourth parallel RC section. This value is equal to R*C and affects the dynamics of the RC section.

Dependencies

To use this parameter, set the Charge dynamics parameters to Four time-constant dynamics or Five time-constant dynamics.

Fifth polarisation resistance - fifth RC resistance
0.005 ohms (by default) | positive number.

The resistance of the fifth parallel RC section. This parameter primarily affects the ohmic losses of the RC section.

Dependencies

To use this parameter, set the Charge dynamics parameter to Five time-constant dynamics.

Fifth time constant is the fifth RC time constant
30 s (by default) | positive number.

The time constant of the fifth parallel RC section. This value is equal to R*C and affects the dynamics of the RC section.

Dependencies

To use this parameter, set the Charge dynamics parameters to Five time-constant dynamics.

Fade

To use these parameters, set Battery charge capacity to Finite.

Battery fade - select whether or not to simulate battery degradation on charge and discharge
Off (By default) | On

If checked, the unit simulates battery fade:

Disabled - battery characteristics are independent of the number of charge-discharge cycles.
On - the battery characteristics change depending on the number of completed charge-discharge cycles. Selecting this option opens additional parameters in this section that define the battery characteristics after a certain number of discharge cycles. The unit uses the values of these parameters to calculate the scaling factors k₁~, k₂~ and k₃~.

See Battery Fade Modelling for more information.

Number of discharge cycles, N - number of completed charge-discharge cycles
100 (By default) | `positive number

The number of charge-discharge cycles after which the other parameters in this section are measured. It defines the scaling factors k₁, k₂ and k₃ used in modelling battery extinction.

Dependencies

To use this parameter, select the check box for the Battery fade parameters.

Cell capacity after N discharge cycles - maximum battery capacity after N discharge cycles
45 A*h (by default) | positive number

Maximum battery charge, in ampere-hours, after the number of discharge cycles specified by the Number of discharge cycles, N parameters.

Dependencies

To use this parameter, select the checkbox for the Battery fade parameter.

Internal resistance after N discharge cycles - internal resistance of the battery after N discharge cycles
2.02 ohms (by default) | positive number.

The internal resistance of the battery after the number of discharge cycles specified by the Number of discharge cycles, N parameters.

Dependencies

To use this parameter, tick the Battery fade parameter and uncheck the Current Directionality parameter under Main.

Average internal resistance after N discharge cycles - average internal resistance of the battery after N discharge cycles
2.02 ohms (by default) | positive number.

Average battery internal resistance on charge and discharge after the number of discharge cycles specified by the Number of discharge cycles, N parameters.

Dependencies

To use this parameter, select the checkboxes for the Battery fade parameter and for the Current Directionality parameter under Main.

Voltage V1 at charge AH1 after N discharge cycles - output voltage at charge level AH1 after N discharge cycles
10.35 V (by default) | positive number.

Output voltage of the fundamental battery model at charge level AH1 after the number of discharge cycles specified by the parameter Number of discharge cycles, N.

Dependencies

To use this parameter, select the checkbox for the Battery fade parameters.

Calendar Aging

To use these parameters, set Battery charge capacity to Finite.

Calendar aging - calendar aging capability
Disabled (By default) | On

If the checkbox is selected, the unit uses calendar aging of the battery.

Storage condition - storage conditions
Fixed open-circuit voltage (by default) | Fixed state of charge.

Select the parameter that determines the state of charge during storage - open-circuit voltage or state of charge during storage.

Dependencies

To use this parameter, select the Calendar aging checkbox for the Calendar aging parameter.

Normalised open-circuit voltage during storage, V/Vnom - normalised open-circuit voltage during storage
0.9 (By default) | scalar

Normalised open-circuit voltage during storage.

Dependencies

To use this parameter, select the Calendar aging check box and set the Storage condition parameters to Fixed open-circuit voltage.

Open-circuit measurement temperature - open-circuit temperature
298.15 K (by default) | positive number.

The temperature at which the open-circuit voltage measurements were taken.

Dependencies

To use this parameter, open the unit’s thermal port, select the check box for the Calendar aging parameter, and set the Storage condition parameter to `Fixed open-circuit voltage'.

State of charge during storage (%) - percentage state of charge during storage
50 (By default) | positive number

State of charge during storage, in per cent.

Dependencies

To use this parameter, select the check box for the Calendar aging parameter and set the Storage condition parameter to Fixed state of charge.

Vector of time intervals - vector of time intervals
[0] (By default) | `vector'.

Storage time intervals. This parameters must be equal in size to Vector of temperatures.

Dependencies

To use this parameter, select the check box for the Calendar aging parameters.

Vector of temperatures - storage temperatures
[273] K (by default) | vector

Set of storage temperatures. This parameters must be equal in size to Vector of time intervals.

Dependencies

To use this parameter, select the check box for the Calendar aging parameter.

Linear scaling for voltage, b - linear scaling for voltage
2.2134e6 (by default) | scalar

Linear scaling factor for open circuit voltage.

Dependencies

To use this parameter, select the check box for the Calendar aging parameter.

Constant offset for voltage, c - constant offset for voltage
1.632e6 (by default) | scalar

Constant offset for open circuit voltage.

Dependencies

To use this parameter, select the check box for the Calendar aging parameter.

Temperature-dependent exponential increase, d - temperature-dependent exponential multiplier
0.515833569 (By default) | scalar

Temperature-dependent exponential increase.

Dependencies

To use this parameter, select the checkbox for the Calendar aging parameter.

Time exponent, a - time exponent
0.75 (By default) | scalar

The multiplier of the exponent that defines the time dependence.

Dependencies

To use this parameter, select the checkbox for the Calendar aging parameter.

Temperature Dependence

To use these parameters, set Thermal port to On.

Nominal voltage at second measurement temperature - output voltage with fully charged battery
12 V (By default) | `positive number

Idle voltage at second measurement temperature when the battery is fully charged.

Internal resistance at second measurement temperature - internal resistance of the battery
2.2 ohms (by default) | positive number.

Battery internal resistance at second measurement temperature.

Voltage V1 at second measurement temperature - output voltage at charge level AH1
11.4 V (by default) | positive number.

Output voltage of the main battery model at second measurement temperature and AH1 charge level set by the parameters Charge AH1 at idle voltage V1.

Dependencies

To use this parameter, set the Battery charge capacity parameters to Finite.

Self-discharge resistance at second measurement temperature - resistance reflecting battery self-discharge
2200 ohms (by default) | positive number.

Resistance in the fundamental battery model at second measurement temperature reflecting battery self-discharge.

Dependencies

To use this parameter, select the checkbox for the Self-discharge parameters.

First polarisation resistance at second measurement temperature - first RC resistance at second measurement temperature
0.005 ohms (by default) | positive number.

Resistance of the first parallel RC section at second measurement temperature.

Dependencies

To use this parameter, set the Charge dynamics parameters to One time-constant dynamics, Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics or Five time-constant dynamics.

First time constant at second measurement temperature - first RC time constant at second measurement temperature
30 s (by default) | `positive number

Time constant of the first parallel RC section at second measurement temperature.

Dependencies

Second polarisation resistance at second measurement temperature - second RC resistance at second measurement temperature
0.005 ohms (by default) | positive number.

Resistance of the second parallel RC section at second measurement temperature.

Dependencies

To use this parameter, set the Charge dynamics parameters to Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics or Five time-constant dynamics.

Second time constant at second measurement temperature - second RC time constant at second measurement temperature
30 s (by default) | positive number.

Time constant of the second parallel RC section at second measurement temperature.

Dependencies

To use this parameter, set the Charge dynamics parameters to Two time-constant dynamics, Three time-constant dynamics, Four time-constant dynamics or Five time-constant dynamics.

Third polarisation resistance at second measurement temperature - third RC resistance at second measurement temperature
0.005 ohms (by default) | positive number.

Resistance of the third parallel RC section at second measurement temperature.

Dependencies

To use this parameter, set the Charge dynamics parameters to Three time-constant dynamics, Four time-constant dynamics or Five time-constant dynamics.

Third time constant at second measurement temperature - third RC time constant at second measurement temperature
30 s (by default) | `positive number

Time constant of the third parallel RC section at second measurement temperature.

Dependencies

To use this parameter, set the Charge dynamics parameters to Three time-constant dynamics, Four time-constant dynamics or Five time-constant dynamics.

Fourth polarisation resistance at second measurement temperature - fourth RC resistance at second measurement temperature
0.005 ohms (by default) | positive number.

Resistance of the fourth parallel RC section at second measurement temperature.

Dependencies

To use this parameter, set the Charge dynamics parameters to Four time-constant dynamics or Five time-constant dynamics.

Fourth time constant at second measurement temperature - Fourth RC time constant at second measurement temperature
30 s (by default) | positive number.

Time constant of the fourth parallel RC section at second measurement temperature.

Dependencies

To use this parameter, set the Charge dynamics parameters to Four time-constant dynamics or Five time-constant dynamics.

Fifth polarisation resistance at second measurement temperature - fifth RC resistance at second measurement temperature
0.005 ohm (by default) | positive number

Resistance of the fifth parallel RC section at second measurement temperature.

Dependencies

To use this parameter, set the Charge dynamics parameters to Five time-constant dynamics.

Fifth time constant at second measurement temperature - fifth RC time constant at second measurement temperature
30 s (By default) | `positive number

Time constant of the fifth parallel RC section at second measurement temperature.

Dependencies

To use this parameter, set the Charge dynamics parameters to Five time-constant dynamics.

Second measurement temperature is the temperature at which the unit parameters are measured
273.15 K (by default) | positive number.

The T₂ temperature at which the unit parameters are measured in Temperature Dependence.

Thermal Port

Thermal port - enable thermal port
off (by default) | on

Select this checkbox to enable the block thermal port and simulate battery thermal effects.

Thermal mass - the thermal mass associated with the thermal port
0000 J/K (by default) | `positive number `

The thermal mass associated with the heat port is H. It represents the energy required to raise the temperature of the thermal port by one degree.

Dependencies

To use this parameter, select the checkbox for the Thermal port parameters.

Literature

Ramadass, P., B. Haran, R. E. White, and B. N. Popov. "Mathematical modelling of the capacity fade of Li-ion cells." Journal of Power Sources. 123 (2003), pp. 230-240.
Ning, G., B. Haran, and B. N. Popov. "Capacity fade study of lithium-ion batteries cycled at high discharge rates." Journal of Power Sources. 117 (2003), pp. 160-169.

Examples

Modelling the motion of an electric vehicle