Engee documentation
Notebook

Relativistic addition of velocities on Julia

In the special theory of relativity, the addition of velocities is nonlinear and is described by the formula:

You can represent speeds as quaternions and implement this addition in Julia.

Unlike the usual vector operations, the quaternion formalism:

  1. Automatically takes into account relativistic effects — the nonlinearity of the addition of velocities arises naturally from the algebraic properties of quaternions, excluding the possibility of "mechanical" addition, prohibited by the special theory of relativity.

  2. Ensures geometric integrity — operations with quaternions maintain invariance with respect to rotations of the reference system, which is critically important for problems of astrophysics and quantum mechanics.

  3. Simplifies calculations — one quaternion operation replaces a series of Lorentz matrix transformations, reducing the amount of calculations in complex systems (for example, when modeling the motion of relativistic particles in accelerators).

The Quaternions.jl library

The addition of relativistic velocities using quaternions can be performed using a specialized library for working with these objects.

In [ ]: 
Pkg.add("Quaternions")

Consider a speculative problem where you move relative to an observer at 60% of the speed of light and fire a shot along the axis of motion, with the projectile or bullet moving relative to you at 40% of the speed of light.

We know that the velocity of the projectile relative to the original observer cannot exceed the speed of light, but it will approach it.

In [ ]: 
using Quaternions

# Скорости представим как кватернионы (скалярная часть = 0)
function relativistic_velocity_addition(u, v, c=1.0)
    uv = -((u * v).s)  # кватернионное произведение
    γ = 1 / (1 + uv / c^2)  # релятивистский фактор
    return γ * (u + v)
end

# Пример: две скорости вдоль оси X
u = quat(0, 0.6, 0, 0)  # 0.6c
v = quat(0, 0.4, 0, 0)  # 0.4c

u_plus_v = relativistic_velocity_addition(u, v)
println("Результирующая скорость: ", [u_plus_v.v1, u_plus_v.v2, u_plus_v.v3] )

Результирующая скорость: [0.8064516129032259, 0.0, 0.0]

The result ≈0.806c is the correct relativistic sum for 0.6c+ 0.4C.

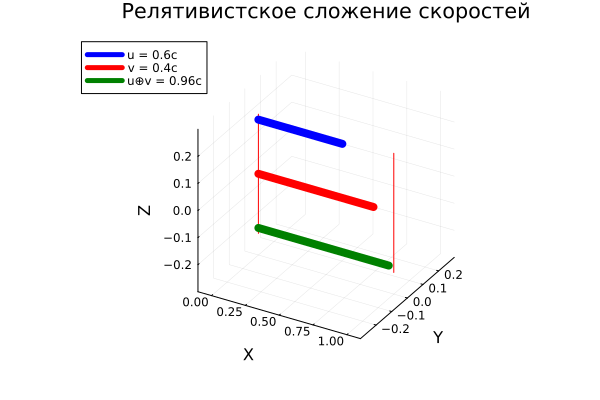
Visualization of the relativistic addition of velocities

At the end of this example, we will create an interactive diagram that can be controlled using convenient sliders. For the sake of speed, we use the backend gr().

In [ ]: 
gr()
Out[0]:
Plots.GRBackend()
In [ ]: 
# Функции для работы с кватернионами
scalar_part(q) = q.s
vector_part(q) = [q.v1, q.v2, q.v3]

# Релятивистское сложение скоростей
function relativistic_velocity_addition(u, v, c=1.0)
    uv = -((u * v).s)  # кватернионное произведение
    γ = 1 / (1 + uv / c^2)  # релятивистский фактор
    return γ * (u + v)
end

# Слайдеры для управления скоростями
# @markdown Скорости обоих тел (в долях от c)
blue_slider = 0.62 # @param {type:"slider",min:0,max:0.99,step:0.01}
red_slider = 0.85 # @param {type:"slider",min:0,max:0.99,step:0.01}

# Создаем фигуру
u = quat(0, blue_slider[], 0, 0)
v = quat(0, red_slider[], 0, 0)
result = relativistic_velocity_addition(u, v)

# Создаем 3D-график
Plots.plot(title="Релятивистское сложение скоростей",
     xlims=(-0.1, 1.1), ylims=(-0.3, 0.3), zlims=(-0.3, 0.3),
     xlabel="X", ylabel="Y", zlabel="Z",
     legend=:topleft)

# Рисуем векторы
Plots.plot!( [0,0], [0,0], [-0.22,0.22], c=:red, label=false )
Plots.plot!( [1,1], [0,0], [-0.22,0.22], c=:red, label=false )

Plots.plot!([0,vector_part(u)[1]], [0,vector_part(u)[2]], [0.2,0.2+vector_part(u)[3]],
        color=:blue, label="u = 0.6c", lw=8)
Plots.plot!([0,vector_part(v)[1]], [0,vector_part(v)[2]], [0,vector_part(v)[3]], color=:red, label="v = 0.4c", lw=8)
Plots.plot!([0,vector_part(result)[1]], [0,vector_part(result)[2]], [-0.2,-0.2+vector_part(result)[3]],
        color=:green, label="u⊕v = $(round(vector_part(result)[1], digits=2))c", lw=8)

# Настройка отображения
Plots.plot!(camera=(30, 30))  # Угол обзора
Out[0]:

Conclusion

The use of quaternions for relativistic addition of velocities is not just a mathematical abstraction, but a powerful tool that preserves the physical essence of phenomena.

Quaternions are especially valuable in tasks where the relationship between orientation and motion is important, from spacecraft navigation to computed tomography. Their use ensures that the calculation results are not only mathematically correct, but also physically meaningful, which makes quaternions an indispensable tool of modern science.