PID Controller
PID controller.
blockType: PIDController
|
PID Controller Path in the library: |
|
Discrete PID Controller Path in the library: |
Description
The PID Controller block implements a PID controller (PID, PI, PD, P only or AND only).
The block output is a weighted sum of the input signal, integral of the input signal and derivative of the input signal. The summation weights are given by proportional, integral and differential coefficients. The first order pole filters the differential component.
The block supports several regulator types and structures. Possible options:
-
Type of regulator (PID, PI, PD, P only or I only).
-
Regulator shape (parallel or ideal).
-
Time domain (continuous or discrete).
-
Initial conditions.
When these parameters are changed, the internal structure of the block changes: the corresponding subsystem variants are activated.
Ports
Input
#
IN_1
—
input signal
scalar | vector | matrix
Details
The difference between the setpoint and the output signal of the controlled system as shown in the figure below:
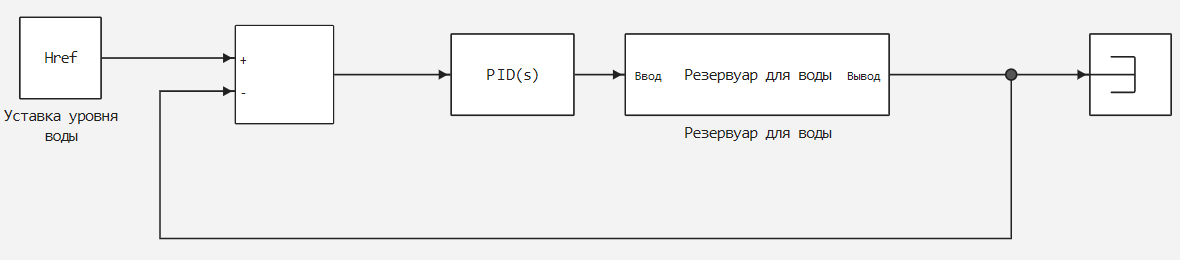
| Data types |
|
| Complex numbers support |
No |
Output
#
OUT_1
—
regulator output
scalar | vector
Details
A controller output that is a weighted sum of the input signal, the integral of the input signal, and the derivative of the input signal. The summation weights are given by the proportional, integral and differential coefficients. Which summands are involved in the summation depends on the value of the parameters Controller.
The output of the controller is a vector signal when the input is a vector signal. In this case the block acts as independent PID controllers, where is the number of signals in the input vector.
| Data types |
|
| Complex numbers support |
No |
Parameters
Main
#
Controller —
controller type
PID | PI | PD | P | I
Details
Specifies the composition of the regulator:
-
PID- proportional, integral and differential parts. -
PI- only proportional and integral parts. -
PD- proportional and differential parts only. -
P- only the proportional part. -
I- only the integral part.
| Values |
|
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
No |
#
Time domain —
discrete or continuous time controller
Discrete-time | Continuous-time
Details
For the value Discrete-time it is recommended to explicitly specify the calculation step for the block. When selecting the value Discrete-time parameters Integrator method and Filter method are also included.
When the block PID Controller is in a model with synchronous state control, you cannot select the Continuous-time.
| Values |
|
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
No |
#
Sample time —
interval between calculation steps
SampleTime (real number / vector of two real numbers)
Details
Specify the interval between calculation steps as a non-negative number. To inherit a calculation step, set this parameter to -1.
It is recommended to explicitly specify the regulator calculation step, especially if the calculation step of subsequent blocks is expected to change. The effect of the regulator coefficients , , and depends on the calculation step. Thus, for a given set of coefficient values, changing the calculation step changes the regulator performance.
Dependencies
To use this parameter, set the parameters Time domain to . Discrete-time.
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
Yes |
#
Form —
regulator structure
Parallel | Ideal
Details
Specifies whether the regulator structure is parallel or ideal:
-
Parallel- the output of the regulator represents the sum of the proportional, integral and differential parts independently weighted by , and , respectively. For example, for a parallel form PID controller with continuous time, the transfer function is of the form:.
For a parallel-form controller with discrete time, the transfer function has the form:
,
where the parameters Integrator method and Filter method define and , respectively.
-
Ideal- proportional gain acts on the sum of all parts. For example, for a PID controller of ideal form with continuous time, the transfer function has the form:For an ideal-form controller with discrete time, the transfer function has the form:
,
where the parameters Integrator method and Filter method define and , respectively.
| Values |
|
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
No |
Controller parameters
#
Proportional (P) —
proportional coefficient
Real number
Details
The finite real value of a pro rata coefficient. When Form:
-
Parallel- the proportional action is independent of the integral and derivative actions. For example, for a parallel PID controller with continuous time the transfer function has the form:.
For a parallel-form controller with discrete time, the transfer function has the form:
,
where the parameters Integrator method and Filter method define and , respectively.
-
Ideal- the proportional coefficient is applied to the sum of all parts. For example, for a PID controller of ideal form with continuous time, the transfer function has the form:.
For an ideal-form controller with discrete time, the transfer function has the form:
,
where parameters Integrator method and Filter method define and respectively.
Dependencies
To use this parameter, set the Controller parameters to . PID, PI, PD or P.
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
Yes |
#
Integral (I) —
integral factor
Real number
Details
The final real value of the integral coefficient.
Dependencies
To use this parameter, set the parameter Controller to . PID, PI or I.
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
Yes |
#
Derivative (D) —
differential coefficient
Real number
Details
The finite real value of the differential coefficient.
Dependencies
To use this parameter, set the parameters Controller to PID or PD.
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
Yes |
#
Filter coefficient (N) —
filtration coefficient of the derivative
Real number
Details
The finite real value of the filter gain. The filter coefficient determines the position of the filter pole in the differential part of the block. The position of the filter pole depends on the parameters Time domain.
When Time domain is set to Continuous-time, the pole position is s = −N.
When Time domain is set to Discrete-time, the pole position depends on the parameters Filter method.
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
Yes |
#
Use filtered derivative —
filter the derivative
Logical
Details
Only for PID controllers with discrete time: Uncheck this box to replace the filtered derivative with an unfiltered value. In this case the differential term of the controller transfer function will become:
.
For PID controllers with continuous time, the derivative component is always filtered.
Dependencies
To use this parameter, set the parameters Time domain to and to . Discrete-time`and set the parameters Controller to `PID or PD.
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
No |
Integrator and Filter methods
#
Integrator method —
integration method in a discrete controller
Forward Euler | Backward Euler | Trapezoidal
Details
In discrete time, the integral term of the controller transfer function is equal to , where depends on the integration method:
-
Forward Euler- direct rectangular (left-handed) approximation:.
This method is best suited for small computation step intervals when the Nyquist limit is large compared to the controller bandwidth. For larger sampling times, the method
Forward Eulercan lead to instability, even in the case of discretising a system that is stable in continuous time. -
Backward Euler- inverse rectangular (right-handed) approximation:.
The advantage of the method
Backward Euleris that discretisation of a stable continuous-time system with usage of this method always yields a stable discrete-time result. -
Trapezoidal- bilinear approximation:.
The advantage of the method
Trapezoidalis that discretisation of a stable continuous-time system with usage of this method always yields a stable discrete-time result. Of all available integration methods, the methodTrapezoidalgives the closest correspondence between the properties of the frequency domain of the discretised system and the corresponding system with continuous time.
Dependencies
To use this parameter, set Time domain to the value of Discrete-time.
| Values |
|
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
No |
#
Filter method —
method of calculating the derivative in a discrete controller
Forward Euler | Backward Euler | Trapezoidal
Details
In discrete time, the differential term of the transfer function of the controller is equal to:
,
where depends on the integration method:
-
Forward Euler- direct rectangular (left-handed) approximation:.
This method is best suited for small computation step intervals when the Nyquist limit is large compared to the controller bandwidth. For larger sampling times, the method
Forward Eulercan lead to instability, even in the case of discretising a system that is stable in continuous time. -
Backward Euler- inverse rectangular (right-handed) approximation:.
The advantage of the method
Backward Euleris that discretisation of a stable continuous-time system with usage of this method always yields a stable discrete-time result. -
Trapezoidal- bilinear approximation:.
The advantage of the method
Trapezoidalis that discretisation of a stable continuous-time system with usage of this method always yields a stable discrete-time result. Of all available integration methods, the methodTrapezoidalgives the closest correspondence between the properties of the frequency domain of the discretised system and the corresponding system with continuous time.
Dependencies
To use this parameter, set Time domain to the value of Discrete-time.
| Values |
|
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
No |
Parameters
#
Differentiator initial condition —
initial value of the derivative
Real number
Details
Initial value of the derivative.
Dependencies
To use this parameter, set Time domain to , uncheck , and set to 0. Discrete-time, uncheck Use filtered derivative, and set the Controller parameters to . PID, PD.
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
Yes |
#
Filter initial condition —
initial filter value
Real number
Details
The initial value of the filter.
Dependencies
To use this parameter, set Time domain to , and set to 0. Discrete-time, select the Use filtered derivative check box, and set the Controller parameters to . PID, PD.
Or set Time domain to Continuous-time, and set the Controller parameters to , , , , , , , , , , and set the parameters to , , . PID, PD.
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
Yes |
#
Integrator initial condition —
integrator initial value
Real number
Details
Initial value of the integrator.
Dependencies
To use this parameter, set the parameters Controller to . PID, PI or I.
| Default value |
|
| Program usage name |
|
| Tunable |
No |
| Evaluatable |
Yes |