Modelling of pipeline pressure control
This example demonstrates the modelling of pressure control in a pipeline.
Working principle of the model
The pipeline is described by blocks of the physical modelling library, in particular, the Volume block is responsible for its volume.
Through Valve 1 the liquid flows from Source to Volume. This in turn is connected to a Pressure sensor, from which the signal is fed to the control system represented by an adder, a setpoint adjuster and a PID controller.
Schematic diagram of the model:
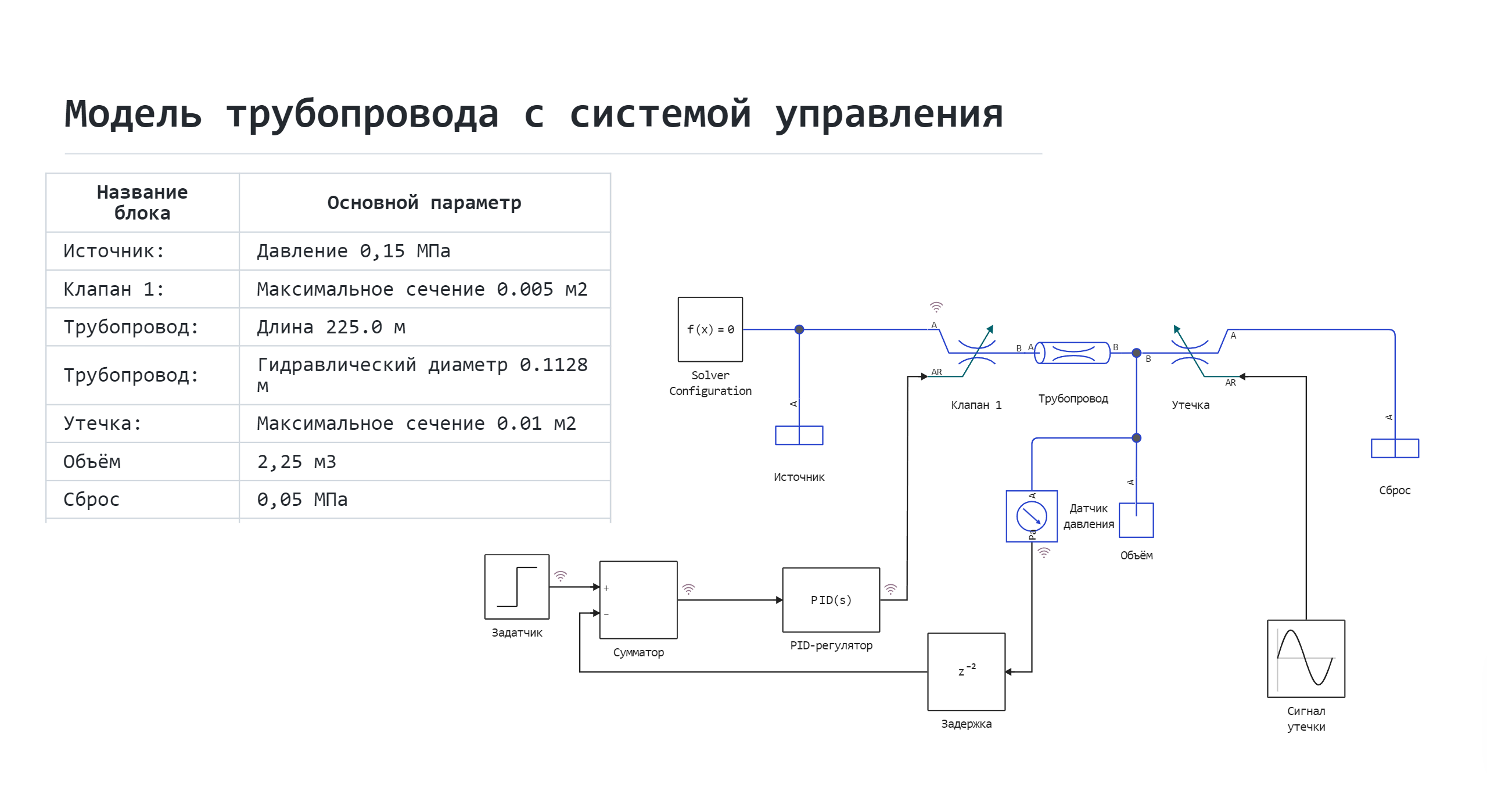
The PID controller sends a control signal to Valve 1 to open or close, providing pressure regulation.
To the right of the Volume block, in the fluid path, is the Leak block, which is, like Valve 1, a controlled throttle.
The Leak block creates some "random" fluid flow from the simulated pipeline.
The fluid passing through this block eventually enters the Discharge, which is described by an infinite reservoir with a given pressure.
Boundary conditions
- At the source, the pressure is always maintained at 151.3 kPa.
- In the reservoir, which characterises the space where the liquid is discharged through a leak, the pressure is always 50 kPa.
Initial conditions:
- The initial pressure in the pipeline is 100 kPa.
- The setpoint signal is 100000, which in the context of regulation means 100 kPa.
Define the function to load and run the model:
function start_model_engee()
try
engee.close("liquid_pressure_regulator", force=true) # закрытие модели
catch err # в случае, если нет модели, которую нужно закрыть и engee.close() не выполняется, то будет выполнена её загрузка после catch
m = engee.load("$(@__DIR__)/liquid_pressure_regulator.engee") # загрузка модели
end;
try
engee.run(m) # запуск модели
catch err # в случае, если модель не загружена и engee.run() не выполняется, то будут выполнены две нижние строки после catch
m = engee.load("$(@__DIR__)/liquid_pressure_regulator.engee") # загрузка модели
engee.run(m) # запуск модели
end
end
Running the simulation
try
start_model_engee() # запуск симуляции с помощью специальной функции, реализованной выше
catch err
end;
Selecting the temperature data of the plots from the simout variable and writing them to variables:
sleep(5)
result = simout;
res = collect(result)
Writing the setpoint and pressure sensor signals to variables:
control_signal = collect(res[1])
pressure = collect(res[25])
Visualisation of simulation results
using Plots
plot(control_signal[:,1], control_signal[:,2], label="Задатчик", linewidth=3)
plot!(pressure[:,1], pressure[:,2], label="Датчик давления", linewidth=3)
Conclusion:
In this example, modelling of a physical object with an automatic control system has been demonstrated. The transient time is about 15 s, the pressure stabilises within acceptable limits, its minor fluctuations are related to the leakage of liquid from the pipeline.