Engee documentation
Notebook

Mechanical system with rigid limiter of translational motion

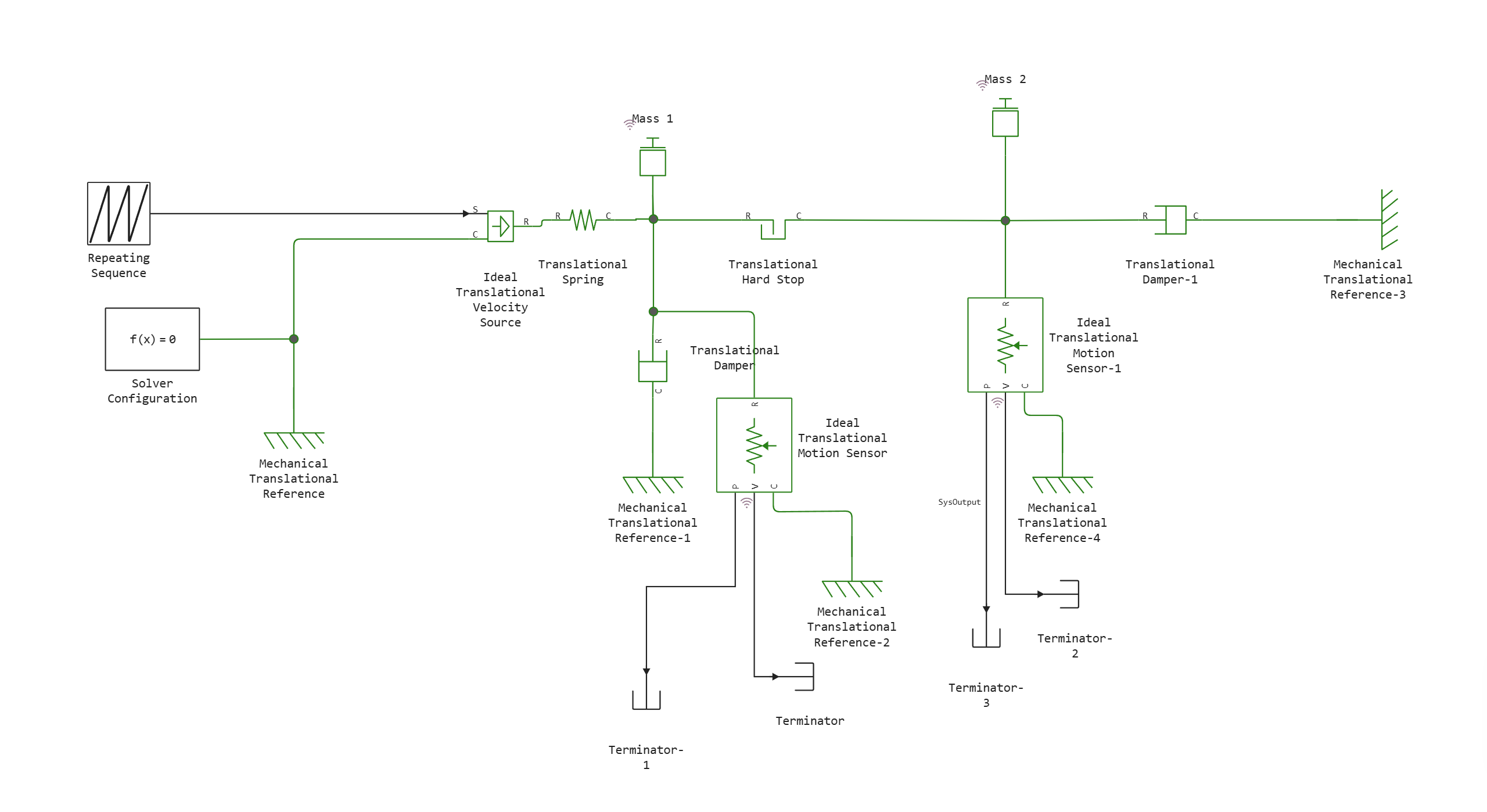
This example shows two masses connected by a rigid limiter. Mass 1 is driven by an ideal source of velocity. When the direction of the input velocity changes, Mass 2 does not move until Mass 1 reaches the other end of the gap modeled by a translational rigid limiter.

Model diagram:

mechanical_system_translational_hardstop--1733299118648.png

Defining the function to load and run the model:

In [ ]: 
function start_model_engee()
    try
        engee.close("mechanical_system_translational_hardstop", force=true) # closing the model
        catch err # if there is no model to close and engee.close() is not executed, it will be loaded after catch.
            m = engee.load("$(@__DIR__)/mechanical_system_translational_hardstop.engee") # loading the model
        end;

    try
        engee.run(m) # launching the model
        catch err # if the model is not loaded and engee.run() is not executed, the bottom two lines after catch will be executed.
            m = engee.load("$(@__DIR__)/mechanical_system_translational_hardstop.engee") # loading the model
            engee.run(m) # launching the model
        end
end
Out[0]:
start_model_engee (generic function with 1 method)

Launching the model:

In [ ]: 
try
    start_model_engee() # running the simulation using the special function implemented above
    catch err
    end;

Output of simulation results from the simout variable:

In [ ]: 
res = collect(simout)
Out[0]:
8-element Vector{WorkspaceArray}:
 WorkspaceArray{Float64}("Mass 2.flange.v")
 WorkspaceArray{Float64}("Mass 2.F")
 WorkspaceArray{Float64}("Mass 2.v")
 WorkspaceArray{Float64}("Mass 1.flange.v")
 WorkspaceArray{Float64}("mechanical_system_translational_hardstop/SysOutput")
 WorkspaceArray{Float64}("Mass 1.F")
 WorkspaceArray{Float64}("mechanical_system_translational_hardstop/Ideal Translational Motion Sensor.2")
 WorkspaceArray{Float64}("Mass 1.v")

Writing results to variables:

In [ ]: 
P1 = collect(res[7]); # Mass transfer 1 "mechanical_system_translational_hardstop/Ideal Translational Motion Sensor.2")
P2 = collect(res[5]); # Moving mass 2 ("mechanical_system_translational_hardstop/SysOutput")
v1 = collect(res[8]); # Mass velocity 1
v2 = collect(res[3]); # Mass velocity 2

Simulation results:

In [ ]: 
using Plots
plot(P1[:,1], P1[:,2], linewidth=3, xlabel= "Time, from", ylabel= "Displacement, m", legend=:bottomright, label="Weight 1")
plot!(P2[:,1], P2[:,2], linewidth=3, label="Weight 2")
Out[0]:
In [ ]: 
using Plots
plot(v1[:,1], v1[:,2], linewidth=3, xlabel= "Time, from", ylabel= "Speed, m/s", legend=:bottomright, label="Weight 1")
plot!(v2[:,1], v2[:,2], linewidth=3, label="Weight 2")
Out[0]:

Blocks used in example