Engee documentation
Notebook

Physical model of the temperature field of a flat radiation heat exchanger

In this example, we will consider modeling a flat radiation heat exchanger, similar to that presented in the example /user/start/examples/math_and_optimization/heat_exchanger/heat_exchanger.ngscript, using the blocks of the thermophysics library.

The design scheme of the heat exchanger divided into elements:

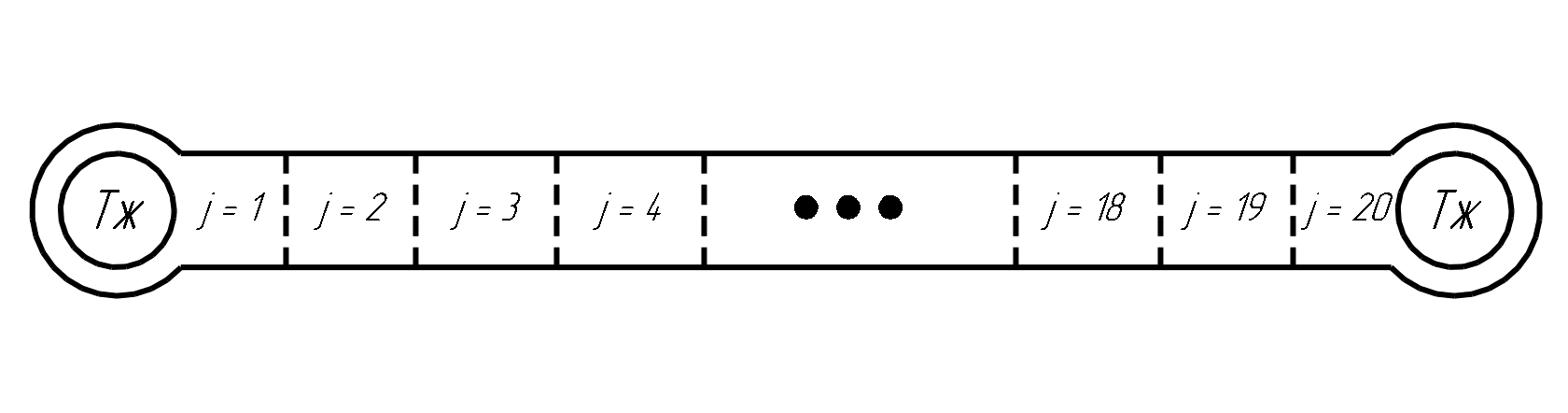
heatex2.png

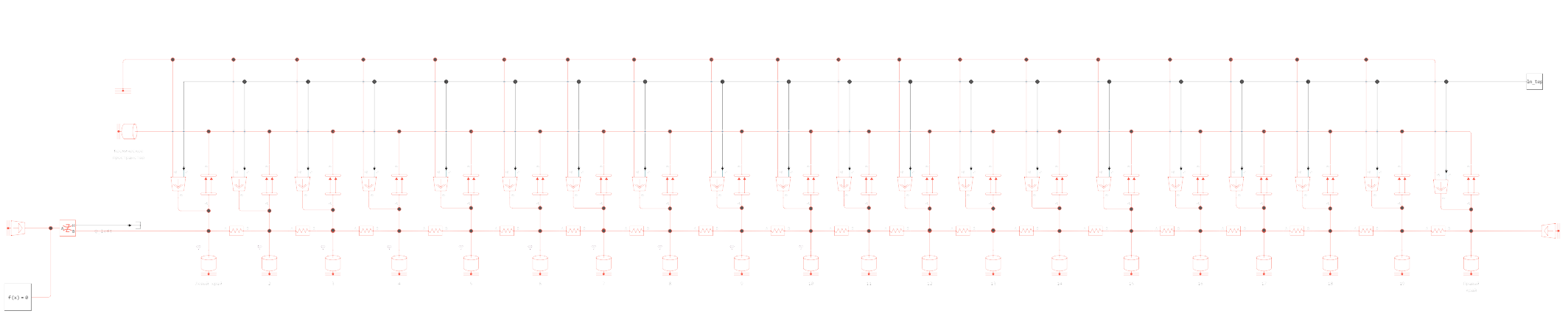
When implementing this calculation scheme in Engee, elements of the thermal library of physical modeling were used.

The key blocks used in the model are:

  • Temperature Source a block that implements boundary conditions for the temperature of the extreme (1 and 20) sections of the heat exchanger
  • Controlled Heat Flow Rate Source a heat source that characterizes the heat flow from the Sun
  • Thermal Mass in this model is used as an element of the heat exchanger, in accordance with the design scheme, as well as as an element of outer space into which heat is radiated from a heat exchanger
  • Radiative Heat Transfer characterizes the transfer of heat by radiation from the heat exchanger element into outer space.
  • Thermal Resistance thermal resistance between the elements

The Engee model:

heat_exchanger_physmod--1711717088198_3.png

Boundary conditions

In the first and last sections of the heat exchanger, the temperature is constant and is equal to 293.15 K.:

,

.

Initial conditions:

The temperature at each point of the heat exchanger at the initial time is 293.15 K.:

.

Determination of the parameters of the heat exchanger elements and the environment:

In [ ]: 
init_T = 293.15 # the initial temperature of each section of the heat exchanger
res = 0.167 # thermal resistance between heat exchanger sections
mass = 0.003375 # mass of the heat exchanger element
c = 903.7 # heat capacity of the material (aluminum)
F = 0.00025 # the surface area of the element for calculating thermal radiation
cosm_tepl = 10000000.0 # the heat capacity of outer space (conditionally infinite)
sigma = 5.6e-8; # the Stefan-Boltzmann constant
soln_teplo = 0.0400047; # heat flow from the Sun absorbed by the heat exchanger section

Defining the function to load and run the model:

In [ ]: 
function start_model_engee()
    try
        engee.close("heat_exchanger_physmod", force=true) # closing the model
        catch err # if there is no model to close and engee.close() is not executed, it will be loaded after catch.
            m = engee.load("/user/start/examples/physmod/heat_exchanger_physmod/heat_exchanger_physmod.engee") # loading the model
        end;

    try
        engee.run(m) # launching the model
        catch err # if the model is not loaded and engee.run() is not executed, the bottom two lines after catch will be executed.
            m = engee.load("/user/start/examples/physmod/heat_exchanger_physmod/heat_exchanger_physmod.engee") # loading the model
            engee.run(m) # launching the model
        end
end
Out[0]:
start_model_engee (generic function with 1 method)

Running the simulation

In [ ]: 
try
    start_model_engee() # running the simulation using the special function implemented above
    catch err
    end;

Extracting site temperature data from the simout variable and writing it to variables:

In [ ]: 
sleep(5)
T1 = simout["heat_exchanger_physmod/Left edge.T"].value[:] # output of data on the temperature of the first section
T2 = simout["heat_exchanger_physmod/2.T"].value[:] # output of data on the temperature of the second section
T3 = simout["heat_exchanger_physmod/3.T"].value[:]
T4 = simout["heat_exchanger_physmod/4.T"].value[:]
T5 = simout["heat_exchanger_physmod/5.T"].value[:]
T6 = simout["heat_exchanger_physmod/6.T"].value[:]
T7 = simout["heat_exchanger_physmod/7.T"].value[:]
T8 = simout["heat_exchanger_physmod/8.T"].value[:]
T9 = simout["heat_exchanger_physmod/9.T"].value[:]
T10 = simout["heat_exchanger_physmod/10.T"].value[:]
Out[0]:
WorkspaceArray{Float64}("heat_exchanger_physmod/10.T").value

Visualization of simulation results

Plotting the time decision for segments 1 to 10 (from the left edge to the middle of the heat exchanger):

In [ ]: 
plot()
plot(collect(0:0.01:100.0), T1, label="1 segment")
plot!(collect(0:0.01:100.0), T2, label="2 segment")
plot!(collect(0:0.01:100.0), T3, label="3 segment")
plot!(collect(0:0.01:100.0), T4, label="4 segment")
plot!(collect(0:0.01:100.0), T5, label="5 segment")
plot!(collect(0:0.01:100.0), T6, label="6 segment")
plot!(collect(0:0.01:100.0), T7, label="7 segment")
plot!(collect(0:0.01:100.0), T8, label="8 segment")
plot!(collect(0:0.01:100.0), T9, label="9 segment")
plot!(collect(0:0.01:100.0), T10, label="10 segment")
Out[0]:

Conclusion:

In this example, a simulation of a flat heat exchanger created from blocks of a thermal library was demonstrated. The simulation results are numerically close to those obtained by numerically solving the differential equation of thermal conductivity, from which it can be concluded that the approach involving the representation of sections as separate thermal masses is correct.

Blocks used in example