Modelling an unstable multivibrator
This example will demonstrate the modelling of an unstable multivibrator.
An unstable multivibrator is an auto-oscillating circuit that generates continuous rectangular pulses. It has no steady states and automatically switches between two transistors, generating a periodic signal.
Multivibrators can be used to generate clock signals in a variety of systems.
Mathematical description
The duration of pulses and pauses is determined by the RC circuits in the base circuits of the transistors.
The duration of the "ON" state for each transistor:
Total oscillation period (with symmetrical circuit):
Frequency of signals:
Schematic of the model:
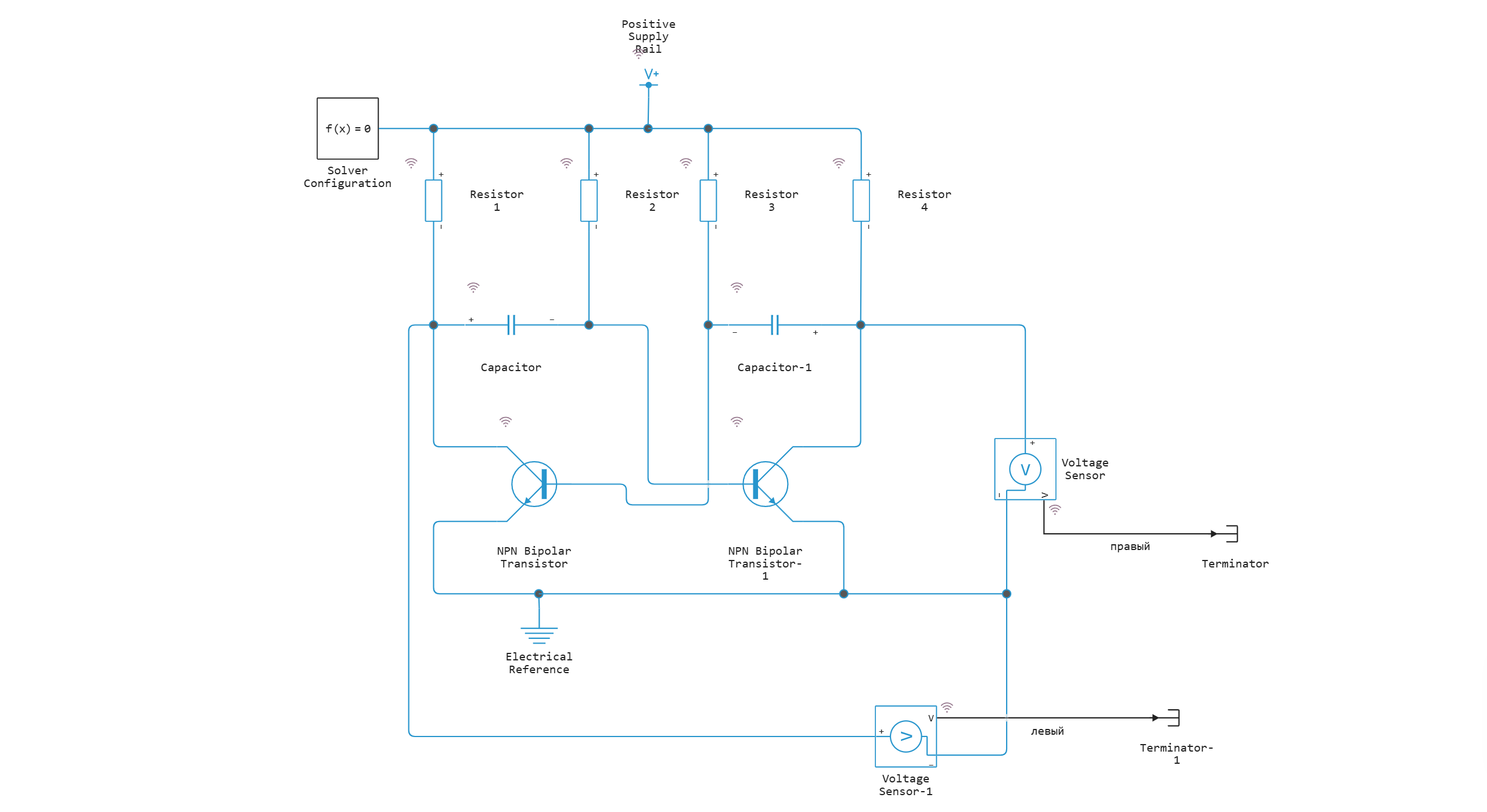
Define the function to load and run the model:
function start_model_engee()
try
engee.close("npn_transistor", force=true) # закрытие модели
catch err # в случае, если нет модели, которую нужно закрыть и engee.close() не выполняется, то будет выполнена её загрузка после catch
m = engee.load("$(@__DIR__)/astable_multivibrator.engee") # загрузка модели
end;
try
engee.run(m, verbose=true) # запуск модели
catch err # в случае, если модель не загружена и engee.run() не выполняется, то будут выполнены две нижние строки после catch
m = engee.load("$(@__DIR__)/astable_multivibrator.engee") # загрузка модели
engee.run(m, verbose=true) # запуск модели
end
end
Running the simulation
start_model_engee();
Write simulation data to variables:
t = simout["astable_multivibrator/правый"].time[:]
V_right = simout["astable_multivibrator/правый"].value[:]
V_left = simout["astable_multivibrator/левый"].value[:]
I_R1 = simout["Resistor 1.i"].value[:]
I_R4 = simout["Resistor 4.i"].value[:]
Data visualisation
using Plots
Visualisation of the collector-emitter voltage on both transistors:
plot(t, V_left, linewidth=2)
plot!(t, V_right, linewidth=2)
Visualisation of the current on the resistors connected to the collectors of the transistors:
plot(t, I_R1, linewidth=2)
plot!(t, I_R4, linewidth=2)
Processing of simulation results:
Running the statistics library:
using Statistics
Defining a function to find the frequency and period of voltage fluctuations:
function calculate_oscillation_properties(time::Vector{T}, x::Vector{T}) where T <: Real
# Проверка длины векторов
if length(time) != length(x)
error("Векторы времени и сигнала должны быть одинаковой длины")
end
n = length(time)
n < 2 && return (NaN, NaN) # Недостаточно данных
# Находим среднее значение сигнала
avg = sum(x) / n
# Ищем моменты пересечения среднего значения снизу вверх
up_crossings = T[]
for i in 2:n
if x[i-1] < avg && x[i] >= avg
# Линейная интерполяция для точного определения времени пересечения
t = time[i-1] + (time[i] - time[i-1]) * (avg - x[i-1]) / (x[i] - x[i-1])
push!(up_crossings, t)
end
end
# Проверка достаточного количества пересечений
length(up_crossings) < 2 && return (NaN, NaN)
# Расчёт периодов (в единицах времени)
periods = diff(up_crossings)
mean_period = mean(periods)
frequency = 1 / mean_period
return "Частота колебаний: $frequency Гц. Период колебаний: $mean_period с."
end
Applying the function to a vector of voltage values (any signals can be substituted):
calculate_oscillation_properties(collect(t)[:,1], collect(V_left)[:,1])
Conclusions:
In this example we have considered a model of unstable multivibrator, where the key elements determining the frequency and period of oscillations are base resistors (R2, R3) and capacitors forming time-delay RC circuits. Collector resistors (R1, R4) do not influence the frequency of the signal - their role is reduced to limiting the current through the transistors and forming the amplitude of the output voltage.