Measurement-based parameterisation of SDPMs
This example shows how to parameterise a permanent magnet synchronous motor (PMSM) based on experimental measurements.
In order to determine the parameters of a permanent magnet synchronous motor, we will perform three experiments. The desired motor parameters are known to us in advance and we will compare them with the values obtained from the experiments.
Data from the motor documentation:
nPolespairs = 2; # Количество пар полюсов
iRated = 2.5; # Ток при номинальной скорости и нагрузке (А)
rpmRated = 7500; # Номинальная скорость (об/мин)
torqueRated = 0.07; # Крутящий момент при номинальной скорости (Н·м)
torqueStall = 0.28; # Заданный крутящий момент (Н·м)
iStall = 8.5; # Пиковый ток (А)
inertia = 5e-6; # Момент инерции (кг·м2)
viscousDamping = 1.13e-6; # Коэффициент вязкого трения
staticFriction = 7e-4; # Коэффициент сухого трения
coulombFriction = 0.8*staticFriction; # Коэффициент кулоновского трения
R = 3.43; # Сопротивление (Ом)
L = 0.53e-3; # Индуктивность (Гн)
# Параметры блока PMSM (СДПМ)
torqueConstant = 2/3*torqueStall/iStall; # Постоянная момента (Нм/А)
emfConstant = torqueConstant; # Постоянная противо-ЭДС (В∙с/рад)
PM = torqueConstant/nPolespairs; # Потокосцепление постоянного магнита (Вб)
# Параметры и флаги контроллера
rpmDemand = rpmRated; # Заданная скорость (об/мин)
enableDrive = 1; # Включение управления
dt = 1e-4; # Период дискретизации контроллера (с)
Test 1: Determination of R and L with the rotor stationary
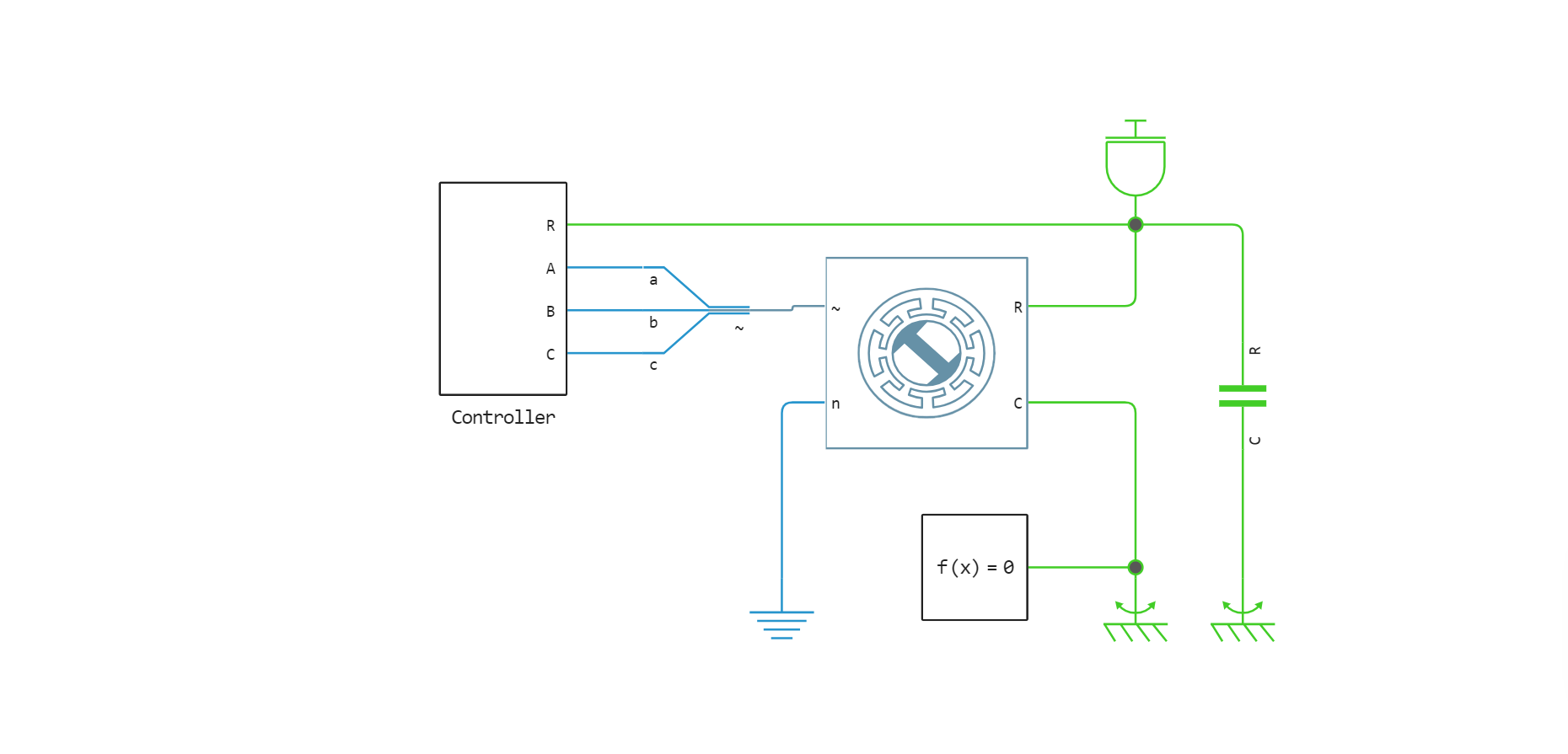
The first experiment is carried out on a motor with locked rotor. A voltage step is applied between the phases and the transient response is studied. The resulting time constant τ is determined by the stator resistance and inductance values:
Set the initial angle of rotation of the rotor:
rotorangle = -90/(nPolespairs);
Run the model:
if "PMSMFromMeasurement1" in [m.name for m in engee.get_all_models()]
m = engee.open( "PMSMFromMeasurement1" ) # загрузка модели
else
m = engee.load( "PMSMFromMeasurement1.engee" )
end
results1 = engee.run(m, verbose=true)
Reading data from the model:
t = results1["uab"].time; # Время
uab_1 = results1["uab"].value; # Напряжение между фазами a и b
ia = results1["ia"].value; # Ток на фазе a
Calculate the resistance from the values, steady-state voltage and current.
Windings a and b in the experiment are connected in series, so we divide the obtained resistance by 2:
R_e = uab_1[end] / ia[end] / 2;
Let's find the time constant of the circuit - this is the time for which the current reaches the value of the steady-state current:
idx = findfirst(x -> x >= (0.63 * ia[end]), ia);
tau = t[idx];
From the formula express and calculate the inductance L:
L_e = R_e * tau;
Expected transient:
iEstimated = uab_1[end] / (2 * R_e) * (1 .- exp.(-t .* R_e ./ L_e));
In the graph below you can compare the measured current from the model and the current graph obtained from the calculations.
using Plots
plotlyjs();
plot(t, ia, xlabel="Время, c", ylabel="Ток, А", w = 2, label="Измеренный ток", linecolor =:blue)
plot!(t, iEstimated, xlabel="Время, c", ylabel="Ток, А", w = 2, label="Ожидаемый ток", linecolor =:green)
plot!([tau, tau], [0, ia[end]], linecolor =:red, line =:dashdot, label="τ" )
xlims!(0, 10*tau) # Установка пределов оси x
ylims!(0, ia[end]) # Установка пределов оси y
annotate!(0.0008, 4.5, text(string("R эталонное = ", R, " Ом"), :left, 10))
annotate!(0.0008, 4, text(string("R измеренное = ", round(R_e, digits=2), " Ом"), :left, 10))
annotate!(0.0008, 3.5, text(string("L эталонная = ", L*1000, " мГн"), :left, 10))
annotate!(0.0008, 3, text(string("L измеренная = ", round(L_e*1000, digits=2), " мГн"), :left, 10))
annotate!(tau, 1, text(string("Измеренная постоянная времени = ", round(1000*tau, digits=3), " мc"), :left, 10))
Test 2. Determining the constant counter-EMF
In the second experiment, the motor rotates without an electrical load. This makes it possible to estimate the counter-EMF constant.
Note that the counter-EMF constant expressed in SI units is equal to the motor torque constant, so only one constant is calculated in this example.
Running the model:
if "PMSMFromMeasurement2" in [m.name for m in engee.get_all_models()]
m = engee.open( "PMSMFromMeasurement2" ) # загрузка модели
else
m = engee.load( "PMSMFromMeasurement2.engee" )
end
results2 = engee.run(m, verbose=true)
Reading data from the model:
t = results2["uab"].time; # Время
uab_2 = results2["uab"].value; # Напряжение a-b
Determining the counter-EMF constant
The counter-EMF constant can be calculated using the formula:
where is the voltage drop across phase a of the motor,
- angular speed of the motor shaft.
The torque constant is equal to the counter-EMF constant expressed in SI units.
wRef = rpmRated*2*pi/60; # Угловая скорость ротора (рад/с)
vPeakLL = maximum(abs.(uab_2)); # Пиковое линейное напряжение (В)
vPeakLN = vPeakLL/sqrt(3); # Пиковое напряжение фаза-нейтраль (В)
emfConstantE = vPeakLN/wRef; # wq константы противо-ЭДС
The graph below shows the counter-EMF occurring when the experimental motor is travelling at rated speed.
The number of pole pairs can be determined by counting the number of periods of current change per rotor revolution.
plot(t, uab_2, xlabel="Время, c", ylabel="Противо-ЭДС", label="Противо-ЭДС экспериментального двигателя", w = 2)
annotate!(0.0013, -20, text(string("Константа противо-ЭДС эталонная = ", round(emfConstant,digits=4), " В∙с/рад"), :left, 10))
annotate!(0.0013, -25, text(string("Константа противо-ЭДС измеренная = ", round(emfConstantE,digits=4), " В∙с/рад"), :left, 10))
3 Determination of friction coefficients and moment of inertia
In the third experiment, the unloaded motor is controlled by the controller.
In the previous experiment, the torque constant was obtained. This can be used to calculate the friction coefficients by converting the stator currents.
Variables required for modelling the controller:
rpm2rad = 2*pi/60;
rad2rpm = 60/(2*pi);
powermax = torqueRated*rpmRated*2*pi/60;
Kp = 0.01;
Ki = 2.0;
ts = 0.0001;
t2eq_Iq = 2/(3*nPolespairs*PM);
Measure the mechanical torque required to maintain a constant speed at four different speeds.
The torque required at lower speeds is primarily to overcome dry friction, at higher speeds it is viscous friction.
The graph shows the measured torques for the four speeds. A straight line is drawn through these points. The zero velocity crossing gives the coefficient of dry friction and the slope gives the coefficient of viscous friction.
function trapz(x, y)
n = length(x)
integral = 0.0
for i in 1:n-1
integral += (x[i+1] - x[i]) * (y[i+1] + y[i]) / 2
end
return integral
end
rpmVec = [0.25, 0.5, 0.75, 1.0]*rpmRated;
trqVec = zeros(size(rpmVec));
for i=1:length(rpmVec)
if "PMSMFromMeasurement3" in [m.name for m in engee.get_all_models()]
m = engee.open( "PMSMFromMeasurement3" ) # загрузка модели
else
m = engee.load( "PMSMFromMeasurement3.engee" )
end
rpmDemand = rpmVec[i];
engee.set_param!("PMSMFromMeasurement3", "StopTime" => 2*60/rpmDemand)
results3 = engee.run(m, verbose=true)
t = results3["ia"].time; # Время из модели
ia_3 = results3["ia"].value; # ток фазы-a из модели
idx = findfirst(x -> x >= (60/rpmDemand), t);
temp = trapz(t[idx:end],(ia_3[idx:end]).^2)
iaRms = sqrt(temp/(t[end]-t[idx]));
trqVec[i] = 3*torqueConstant*iaRms;
end
rpmDemand = rpmRated;
scatter(rpmVec, 1000*trqVec, title="Механические потери крутящего момента", xlabel="Скорость, м/c", ylabel="Момент, мН*м", w = 2, label="Измеренные значения", legend=:bottomright )
using Polynomials
coef = coeffs(fit(2*pi/60*rpmVec, trqVec,1));
estimatedStaticFriction = coef[1];
estimatedViscousDamping = coef[2];
rpmVec0 = [0; rpmVec];
plot!(rpmVec0, 1000*(estimatedStaticFriction.+rpmVec0*2*pi/60*estimatedViscousDamping), label="Линейная аппроксимация")
annotate!(trqVec[end], 2.1, text(string("Коэффициент сухого трения эталонный = ", staticFriction), :left, 10))
annotate!(trqVec[end], 2.0, text(string("Коэффициент сухого трения измеренный = ", round(estimatedStaticFriction,digits=6)), :left, 10))
annotate!(trqVec[end], 1.9, text(string("Коэффициент вязкого трения эталонный = ", viscousDamping), :left, 10))
annotate!(trqVec[end], 1.8, text(string("Коэффициент вязкого трения измеренный = ", round(estimatedViscousDamping, digits=9)), :left, 10))
The second graph shows the motor deceleration test. For this test, the required torque is set to zero or the motor is switched off.
Using the measured deceleration, with the friction and damping torques set, the moment of inertia of the motor rotor can be determined.
enableDrive = 0;
engee.set_param!("PMSMFromMeasurement3", "StopTime" => 2*60/rpmDemand)
if "PMSMFromMeasurement3" in [m.name for m in engee.get_all_models()]
m = engee.open( "PMSMFromMeasurement3" ) # загрузка модели
else
m = engee.load( "PMSMFromMeasurement3.engee" )
end
results4 = engee.run(m, verbose=true)
enableDrive = 1;
t = results4["rpm"].time; # Время из модели
rpm = results4["rpm"].value; # скорость ротора
plot(t, rpm, xlabel="Время, c", ylabel="Скорость (об/мин)", label="Тест замедления", w = 2)
initialTorque = -staticFriction - rpmRated*2*pi/60*viscousDamping;
initialAccel = 2*pi/60*(rpm[end]-rpm[1])/(2*60/rpmDemand);
estimatedInertia = initialTorque/initialAccel;
annotate!(0, 7465, text(string("Момент инерции эталонный = ", inertia, " кг∙м^2"), :left, 10))
annotate!(0, 7460, text(string("Момент инерции измеренный = ", round(estimatedInertia,digits=6), " кг∙м^2"), :left, 10))
Conclusion
In this example, we have determined the parameters of a permanent magnet synchronous motor based on experimental measurements.
For this purpose, we have performed three tests. In the first test we found the resistance and inductance of the motor winding, in the second test we determined the counter-EMF constant, and in the third test we determined the friction coefficients and moment of inertia.
The values found experimentally are comparable to the motor parameters from the documentation.