Engee documentation
Notebook

Car suspension simulation

This example demonstrates the simulation of the car's suspension when hitting an obstacle.

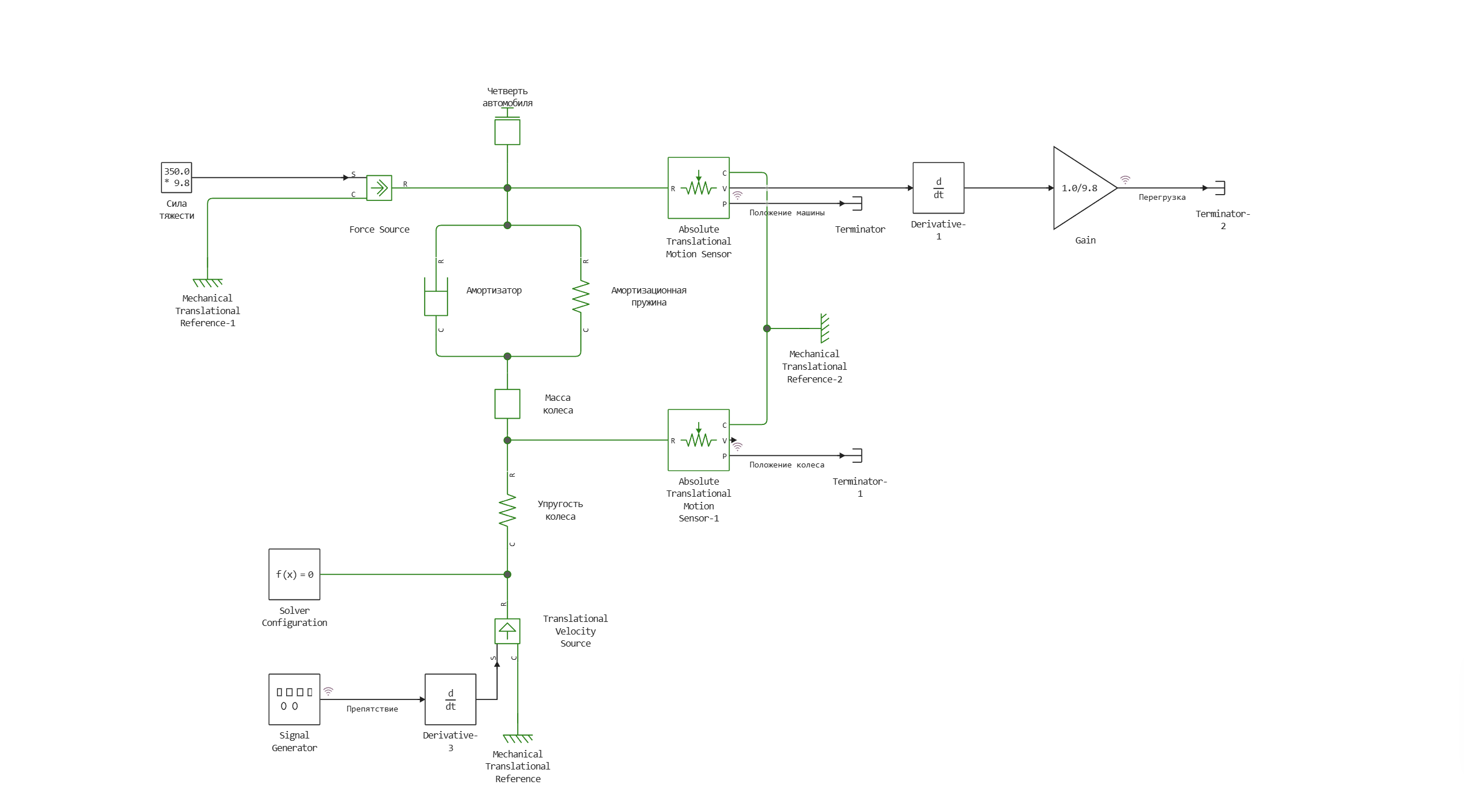
The obstacle is set as a rectangular signal using the Signal Generator block. Using a speed source, the derivative of the signal (speed) is fed to port C of the Translational Spring block, which describes the elastic properties of the wheel.

Translational Spring, in turn, is attached to the mass, which characterizes the inertial properties of the wheel.

The wheel is mounted on suspension elements, a shock absorber and a shock spring, which are represented by blocks Damper and Spring.

The "quarter" of the car itself is attached to other ports of the Damper and Spring blocks.

The wheel has a mass of 50 kg, and the "quarter" of the car is 350 kg.

The obstacle is 5 cm high.

Model diagram:

suspension_physmod--1727789568075.png

Defining the function to load and run the model:

In [ ]: 
function start_model_engee()
    try
        engee.close("suspension_physmod", force=true) # закрытие модели 
        catch err # в случае, если нет модели, которую нужно закрыть и engee.close() не выполняется, то будет выполнена её загрузка после catch
            m = engee.load("$(@__DIR__)/suspension_physmod.engee") # загрузка модели
        end;

    try
        engee.run(m) # запуск модели
        catch err # в случае, если модель не загружена и engee.run() не выполняется, то будут выполнены две нижние строки после catch
            m = engee.load("$(@__DIR__)/suspension_physmod.engee") # загрузка модели
            engee.run(m) # запуск модели
        end
end
Out[0]:
start_model_engee (generic function with 1 method)

Running the simulation

In [ ]: 
try
    start_model_engee() # запуск симуляции с помощью специальной функции, реализованной выше
    catch err
    end;

Extracting data from a simout into a variable:

In [ ]: 
sleep(5)
result = simout;
res = collect(result)
Out[0]:
4-element Vector{WorkspaceArray}:
 WorkspaceArray("suspension_physmod/Положение колеса")
 WorkspaceArray("suspension_physmod/Перегрузка")
 WorkspaceArray("suspension_physmod/Препятствие")
 WorkspaceArray("suspension_physmod/Положение машины")

Writing data about the movement of the wheel and car, as well as about overload, to variables:

In [ ]: 
wheel_pos = collect(res[1])
car_pos = collect(res[4])
overload = collect(res[2]);

Visualization of simulation results

In [ ]: 
using Plots
plot(wheel_pos[:,1], wheel_pos[:,2], linewidth=3, label="Положение колеса, м")
plot!(car_pos[:,1], car_pos[:,2], linewidth=3, label="Положение автомобиля, м")
Out[0]:
In [ ]: 
plot(overload[:,1], overload[:,2], linewidth=3, label="Перегрузка, м/(с^2)")
Out[0]:

Analyzing the graphs, you can see that the overload (the ratio of body acceleration to free fall acceleration) that occurs when hitting an obstacle is slightly more than 2 , affects a quarter of the car in less than 50 ms.

Such an overload is not large and will not have a dangerous effect on a person, nor will it affect the comfort of passengers.

Conclusion:

This example demonstrates the simulation of the car's suspension during a sudden collision with an obstacle. The parameters of the movement of a quarter of the car, as well as the value of overload, which can affect the safety and comfort of passengers, are analyzed.

Blocks used in example