The Venturi effect model

Let's repeat a physical experiment showing the effect of the effect that makes old carburetors, spray guns, refueling guns, aerators, burners and many other devices work.

Description of the model

Isothermal liquid passes from one reservoir to another, both under atmospheric pressure. The boundary conditions on both sides of the tube are set by pumps pumping a given volume of liquid and setting the speed.

With an inlet diameter of = 50 mm, and in the narrow part = 25 mm, taking into account losses in diameter narrowing blocks, the walls of which have a slope of 10 degrees, we observe the following simulation results:

the inlet pressure is 101280 Pa,
pressure in the neck drops to 82872 Pa,
after the passage, the pressure recovered to 97318 Pa (loss of about 4%).

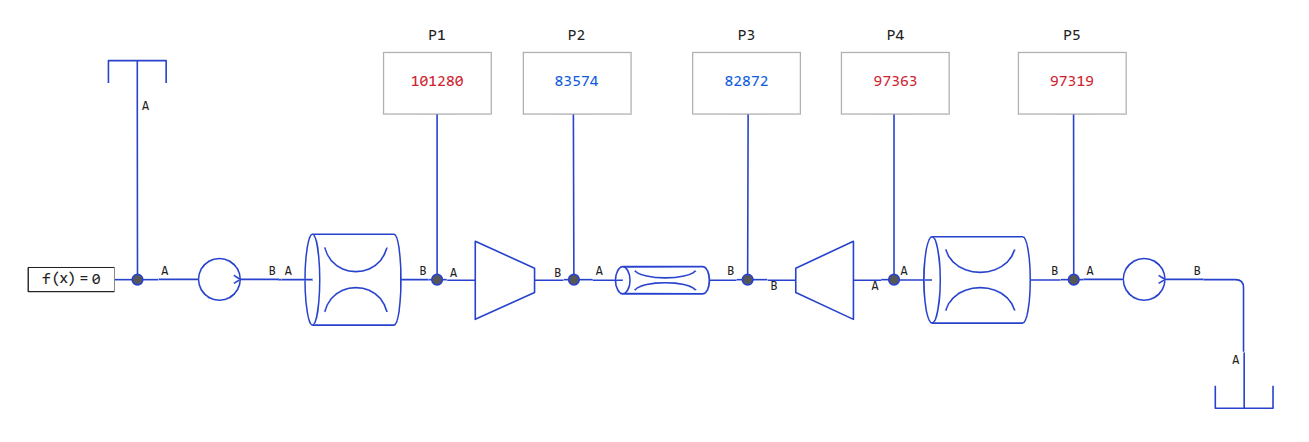
The hydraulic diameter of each section is equated to its geometric diameter (since the pipes have a circular cross-section), and * the total length of local resistances* is equated to zero, so that friction losses in the pipes minimally affect observations.

There are constant volume flow pumps on the sides of the tube, which set the expected flow rate at the inlet and outlet.

You can do without pumps, but then you will need to set the pressure difference between the tanks, and then the inlet and outlet ends of the tube will always show significantly different pressures.

Theoretical calculations

By finding the area of each section we can set the volumetric flow rate of the pumps to , where = 1.5 m/s is the flow rate we have set. Expenditure when is equal to = 1.5 · 3.1416 · (0.05)2 / 4 = 0.002945 m3/s.

The cross-sectional area is calculated inside the corresponding blocks, but we will output it for clarity.:

= 0.002945 / 1.5 ≈ 0.001963 m2

= 3.1416 · (0.025)2 / 4 ≈ 0.0004909 m2

From the equation of continuity we get a velocity inside a narrow tube segment equal to = 0.002945 / 0.0004909 ≈ 6.0 m/s.

From the Bernoulli equation the pressure in the neck should be equal to:

= 101280 + 0.5 · 1000 · (1.5² - 6.0²) = 101280 + 500 · (2.25 - 36) = 101280 - 16875

≈ 84405 Pa

Launching the model

We will get approximately the same data if we run the model.:

model = engee.open("venturi_effect_model.engee");
data = engee.run(model);

for k in sort(collect(keys(data)))
    println(k, " = ", data[k].value[end])
end

P1 = 101280.0432752184
P2 = 83574.9826109334
P3 = 82872.51819827595
P4 = 97363.96480823119
P5 = 97319.00041378968

In an idealized experiment, the outlet pressure would be equal to the inlet pressure, but in real systems, to which the physical model is approximated, there are hydraulic losses.

We disabled dynamic compressibility in pipes to speed up calculations and raised the minimum step of the local solver, since we are working with an isothermal liquid. The loss of 4000 Pa can be explained by friction and vortex formation in the diameter-narrowing blocks.

Conclusion

We have shown how, with the help of physical blocks, it is possible to build a model of the famous physical experiment showing the effect of the Venturi effect, on which the operation of many devices and aggregates is based.