A model of a power steering mechanism

Let's study the model of a simplified version of the hydraulic power steering system.

The system under study

The power steering system converts the driver's force into hydraulic pressure, making it easier to turn the wheels. It is used in cars for comfort and to reduce the burden on the driver. Apart from the fact that the steering wheel reduces the physical effort when turning the steering wheel, this system also improves the accuracy and smoothness of control. Creating a model of such a system will allow optimizing its parameters (torsion bar stiffness, pump performance), studying failures (for example, pressure loss) or testing new solutions (for example, electrohydraulic systems).

Description of the model

The system includes:

Double-sided hydraulic cylinder
4-way control valve
Constant pressure pump
Safety valve

The steering rack acts on the load modeled by the spring and damper.

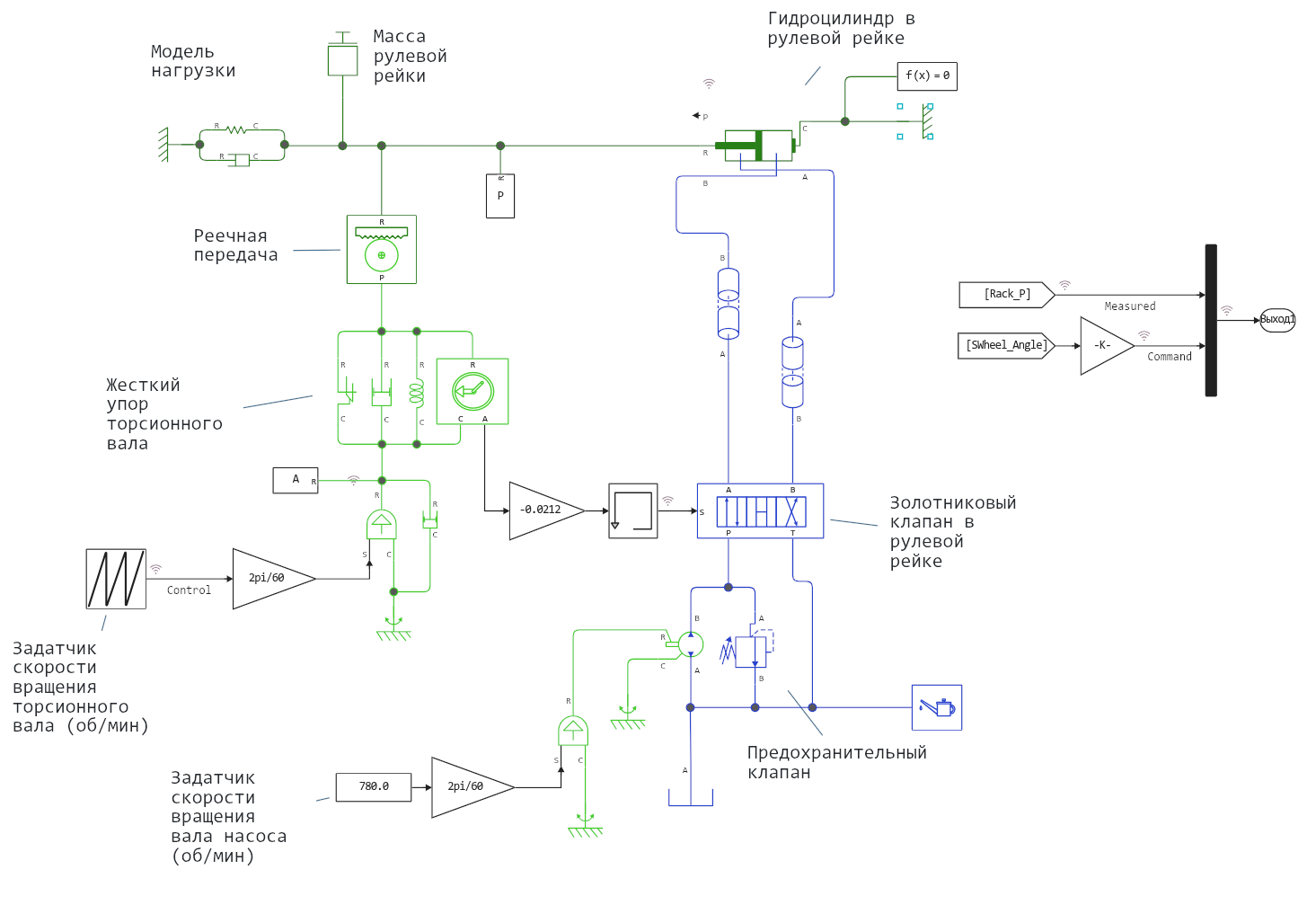
Turning the steering wheel causes twisting of the torsion bar mounted between the steering wheel and the gear rack mechanism. The deformation of the rod is converted into a value expressing the displacement of the stem of the 4-way valve, which connects the cavities of the hydraulic cylinder to the pressure or drain line, depending on the direction of rotation. Between the rotary-mechanical and hydraulic parts of the system there is a "Multiplication by a constant" (Gain) block, which converts the angle of the torsion bar into the degree of valve opening. If the gain of this unit is set to 0, the power steering is turned off.

If the deformation of the torsion bar exceeds 9 degrees, the steering wheel is rigidly connected to the gear through mechanical stops installed parallel to the rod. The hydraulic cylinder moves the steering rack, which causes the torsion bar to reverse until the valve returns to the neutral position.

Running calculations and analyzing the results

Let's run the model using command control to get graphs for the report.:

model_name = "power_assisted_steering_mechanism";
model_name in [m.name for m in engee.get_all_models()] ? engee.open(model_name) : engee.load( "$(@__DIR__)/$(model_name).engee");
res = engee.run( model_name ); # Расчет модели

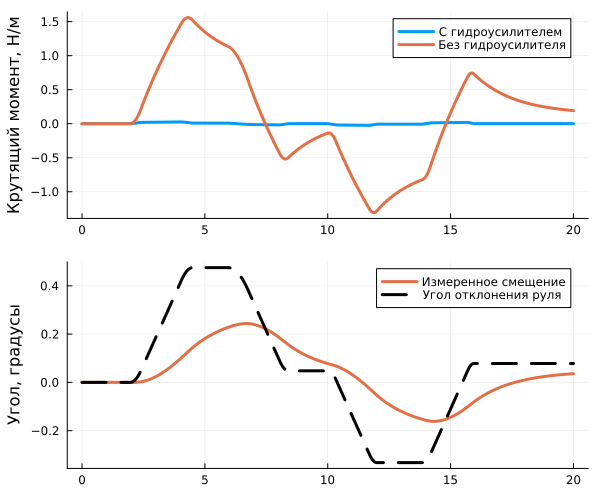
In normal operation, if there is a feedback between the steering angle with a proportional coefficient -0.0212, we get the following graph:

gr()

plot( res["Command"].time, rad2deg.([res["Measured"].value res["Command"].value]),
        label = ["Измеренное смещение" "Угол отклонения руля"],
        ylabel="Угол, градусы",
        lw=3, c=[2 :black], ls=[:solid :dash], size=(600,300) )

gr()

torque_with_as = res["Rack & Pinion.T_pinion"]; # Сохраним значнеие момента на валу руля

plot(
    plot( res["Double-Acting Actuator (IL).port_a.p"].time,
            [res["Double-Acting Actuator (IL).port_a.p"].value res["Double-Acting Actuator (IL).port_b.p"].value],
            label=["Порт А" "Порт Б"], ylabel="Давление, Па",
            lw=3),
    plot( res["Command"].time, rad2deg.([res["Measured"].value res["Command"].value]),
            label = ["Измеренное смещение" "Угол отклонения руля"],
            ylabel="Угол, градусы",
            lw=3, c=[2 :black], ls=[:solid :dash] ),
    size=(600,500), layout=(2,1)
)

We can see how the pressure in each volume inside the hydraulic cylinder changed.

Operation with the power steering turned off

To study the operation with the power steering turned off, we will disconnect the connection between the steering angle sensor and the valve stem, which is now carried out using a proportional coefficient. -0.0212. That is, turning the steering wheel by 90 degrees will shift the rod by 3.33 millimeters in one direction or another.

We will reset this connection using command control.

engee.set_param!( "power_assisted_steering_mechanism/Коэффициент усиления-1", "Gain" => 0 )

Let's implement the previously opened model.

res = engee.run( model_name ); # Расчет модели

The graphs also compare the steering force when the power steering is on and off. When the power steering is turned off, the driver needs to exert significantly more effort without the power steering in order to observe the set angle of rotation of the steering rack.

plot(
    plot(res["Rack & Pinion.T_pinion"].time,
            [torque_with_as.value res["Rack & Pinion.T_pinion"].value],
            ylabel="Крутящий момент, Н/м",
            label=["С гидроусилителем" "Без гидроусилителя"]),
    plot(res["Command"].time, rad2deg.([res["Measured"].value res["Command"].value]),
            label = ["Измеренное смещение" "Угол отклонения руля"],
            ylabel="Угол, градусы", c=[2 :black], ls=[:solid :dash]),
    size=(600,500), layout=(2,1), lw=3
)

In the lower graph, we also notice that the displacement of the wheels is much slower and does not keep up with the command, perhaps this is because the hydraulic pump is still on, and the piston strongly dampens the displacement of the steering rack.

We'll turn on the feedback again so as not to interfere with further experiments.

engee.set_param!( "power_assisted_steering_mechanism/Коэффициент усиления-1",
                   "Gain" => -0.0212 )

What else can be explored on this model?

This model will allow us to debug the model of the digital steering control system, as well as explore the complex effects occurring in the power steering system.:

Investigation of the effect of torsion bar stiffness on steering sensitivity

To do this, add a torsion bar to the simulated element with adjustable stiffness (for example, through a spring with a variable coefficient). This modification will allow us to show how a change in stiffness affects * steering sensitivity* (steering angle before power steering is activated) and * system stability* (the possibility of vibrations when the rod is too soft).

Dynamic damping simulation to eliminate steering fluctuations

To do this, add an active damper to the steering rack system (for example, an electric shock absorber controlled by a speed sensor) to the model. This will allow us to * show how the damper suppresses vibrations* of the steering mechanism during a sharp turn, or * compare the system response* with passive (spring+damper) and active damping.

Simulation of different pump operating modes (constant vs. variable flow)

Replacing a fixed pump with an adjustable one (for example, with proportional control) will allow you to calculate the energy consumption of the system at different speeds (at low speeds more effort is required, at high speeds less), as well as compare the efficiency of the system with a pump of constant and variable capacity.

The effect of backlashes and gaps in the mechanism on steering accuracy

Adding imperfections to the model (for example, dead travel in a gear train or gaps in the joints) will allow you to show how gaps lead to a delay in the reaction of the wheels or visualize shock loads when the direction of rotation abruptly changes.

Conclusion

The implemented model makes it possible to demonstrate a wide range of interesting effects that occur in the power steering system, as well as to begin developing a digital steering control system.