Designing Engee scripts using LaTeX

This example shows a set of commands in the document markup language. , which allow convenient and presentable formatting of mathematical expressions, text and graphs in user-generated interactive scripts Engee.

When designing scripts in Engee, keep in mind that the display of mathematical symbols in expressions embedded in a string, for example: it may differ from the display of characters omitted from the string: $$\int\frac{1}{\sigma {\sqrt{2\pi}}},e^{-{(x-\mu)/2\sigma^{2}}};dx$$

The list of commands shown in the example it is not exhaustive.

1. Signs and symbols

1.1. Number systems

Natural

Natural with zero

Simple ones

Whole ones

Rational

Algebraic
,

Irrational

The real ones

Comprehensive

Quaternions

Octonions (Cayley numbers)

Sedenions

1.2. The Greek alphabet

1.3. Ellipsis and matrices

Ellipsis at the bottom

Ellipsis in the center

Vertical ellipsis

Diagonal ellipsis

Matrices

1.4. Brackets, limiters

Horizontal curly braces

Parentheses

Automatic scaling of brackets

Curly braces

Square brackets

Angle brackets

Straight brackets

Double straight brackets

1.5. Indexes and accents

Indexes

Indexes and degrees

The usual accents

Wide accents

1.6. Other

Hebrew Symbols

Reduced Planck's constant (Dirac's constant)

Some of the more specific signs not shown in this example can be found in the documentation Engee.

2. Arithmetic and elementary algebra

Not equal to

Approximate equality

The identity

Proportionality

Plus or minus

A minus is a plus

The amount

The dot product

Vector and matrix product

Tensor product

Piecemeal work

Composition

Fractions

Obelus

The square root

The root of the nth degree

Exponentiation

Infinity

The actual part

The imaginary part

3. Set theory

The empty set
,

Belongs
Does not belong to

A subset

The superset

A proper subset

Proper superset

Unification

Intersection

Set difference

Function

Display

4. Comparisons and mathematical logic

Less than or equal to

Greater than or equal to

Much less

A lot more

The implication

Equivalence

Quantifier of universality ("for everyone...")

Quantifier of existence
("there is...")
("there is no...")

Definition

Denial of "NOT"

Disjunction of "OR"

Conjunction of "And"

Negation of the disjunction (Pierce's arrow) "OR-NOT"

Negation of the conjunction (Schaeffer's stroke) "AND-NOT"

"EXCLUSIVE OR"

5. Trigonometry and geometry

5.1. Signs

Corner

Perpendicular

Parallel

Proportionality

Degree

Vector

5.2. Functions

The sine

The cosine

Tangent

Cotangence

Arcsinus

The Arccosine

Arctangent

The second

Kosekans

5.3. Hyperbolic functions

The hyperbolic sine

The hyperbolic cosine

The hyperbolic tangent

6. Mathematical analysis

Indefinite integral (inside a paragraph)

Indefinite integral (off)

Definite integral (inside the paragraph)

Double and triple integrals

The closed-loop integral

Partial derivative

The limit

Maximum, minimum

Supremum, infimum

Nabla operator (Hamilton operator)

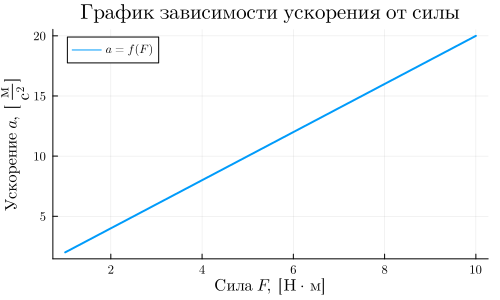
7. in the charts

Using the library LaTeXStrings.jl You can simplify the design of labels and symbols in graphs and markup. .

using Plots, LaTeXStrings
gr(size=([500, 300]))

default(fontfamily="Computer Modern", linewidth=2, framestyle=:nothing, grid=true)

F = collect(1:10);
m = 2;
a = F.*m;

Plots.plot(F, a, label = L"a=f(F)", legend = :topleft)
xlabel!(L"Сила\ F,\ [Н \cdot м]")
ylabel!(L"Ускорение\ a,\ [\frac{м}{с^2}]")
title!(L"График\ зависимости\ ускорения\ от\ силы")

Learn more about the design of Engee charts in it is possible in documentation.