Engee documentation
Notebook

The Van der Pol oscillator

In this example, we will show how to create a dynamics model in Engee that works according to the second-order Van der Pol equation.

Introduction

The Van der Pol oscillator demonstrates the dynamics of not консервативной systems with nonlinear attenuation.

This system can be described by the following equation:

where – coordinate (for example, the position of the oscillator), – damping coefficient. This model is used to study a wide variety of processes in biology and physics, including radio engineering and electronics.

We will model this system using blocks on a canvas for graphical modeling in Engee. In the file van_der_pol_oscillator.engee contains a model of the following type:

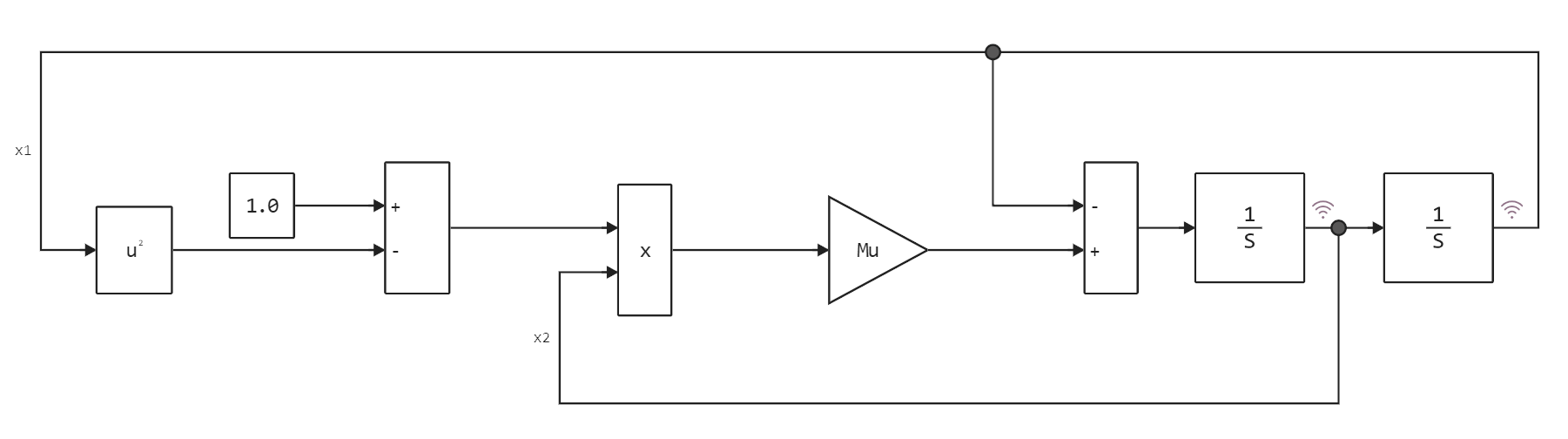
image.png

It has two separate integrators that are responsible for calculating the signals. x1 (coordinate) and x2 (speed).

Starting the model with μ = 1

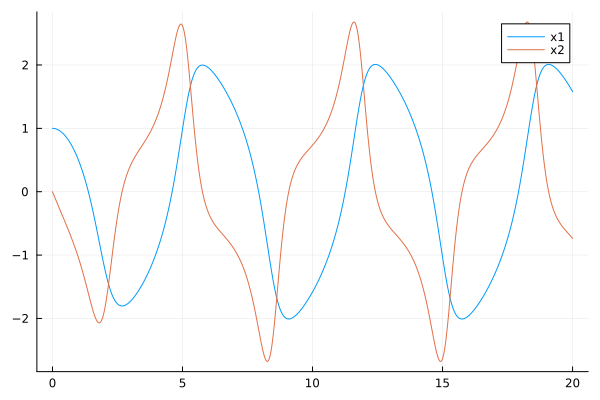
If you run this model with the argument then we will see a self-oscillating mode of operation with nonlinear attenuation. Loading the model:

In [ ]: 
if "van_der_pol_oscillator" in [m.name for m in engee.get_all_models()]
    m = engee.open( "van_der_pol_oscillator" );
else
    m = engee.load( "/user/start/examples/edu/van_der_pol_oscillator/van_der_pol_oscillator.engee" );
end
Out[0]:
"Model(van_der_pol_oscillator)"

Let's run the model in its original form and build a graph.:

In [ ]: 
data = engee.run( m );

plot( data["x1"].value, data["x2"].value )
Out[0]:

We can choose different starting points, changing the initial value of each integrator, but the system will always come to a limit cycle.

A graph can be constructed for each signal separately.

In [ ]: 
plot( data["x1"].time, data["x1"].value, label="x1" )
plot!( data["x2"].time, data["x2"].value, label="x2" )
Out[0]:

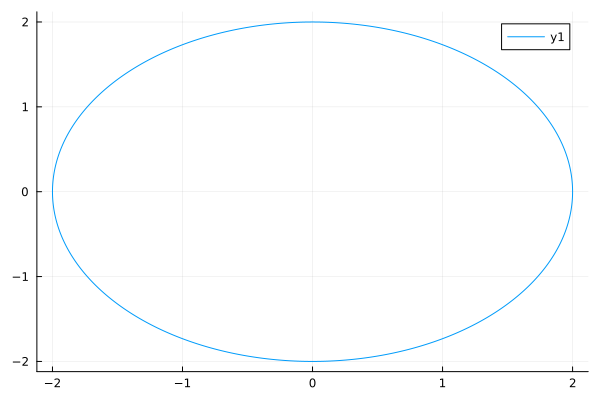
Starting the model with μ = 0

In this mode, the equation of the system is reduced to the equation of a conventional harmonic oscillator.:

Let's set the coefficient set to zero and run the model.

In [ ]: 
engee.set_param!( "van_der_pol_oscillator/Mu", "Gain"=>0 )

data = engee.run( m );
data = engee.run( m );

using Plots
plot( data["x1"].value, data["x2"].value )
Out[0]:

Let's build another graph for this system.:

In [ ]: 
plot( data["x1"].time, data["x1"].value, label="x1" )
plot!( data["x2"].time, data["x2"].value, label="x2" )
Out[0]:

Conclusion

We have seen that graphical modeling in Engee is a convenient way to experiment with the topology of the system, complicate the model, or use it as part of a complex demonstration.

Blocks used in example