Engee documentation
Notebook

Calculating the population using command control in cycles

In this example, the calculation of population dynamics is implemented on the basis of a nonlinear, discrete model.

In the model, the population in a given year p(n) is proportional to the population of the previous year, p(n – 1) multiplied by the rate of reproduction, p. However, resources are limited by L people, thereby creating a negative impact on the population.

The picture below shows the model itself.

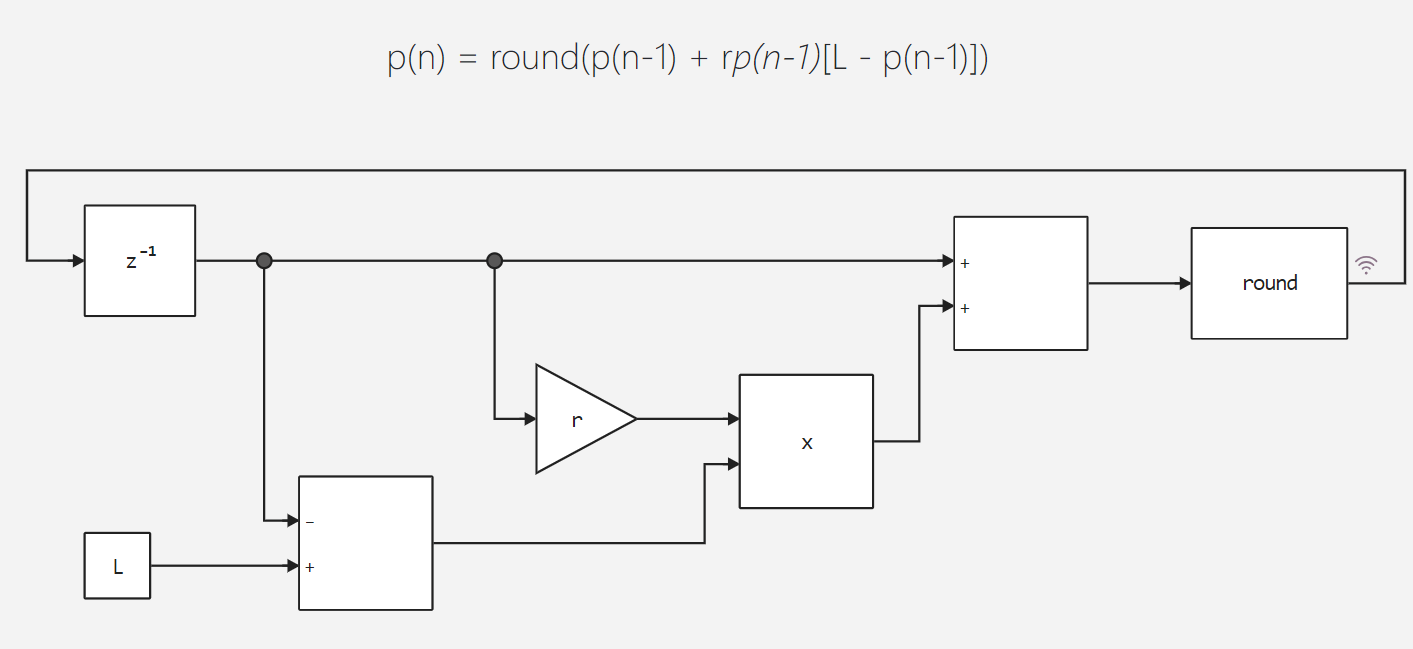
image.png

Next, we will connect the auxiliary function for launching the model and declare the initial states for it.

In [ ]: 
function run_model( name_model)
    
    Path = (@__DIR__) * "/" * name_model * ".engee"
    
    if name_model in [m.name for m in engee.get_all_models()] # Проверка условия загрузки модели в ядро
        model = engee.open( name_model ) # Открыть модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
    else
        model = engee.load( Path, force=true ) # Загрузить модель
        model_output = engee.run( model, verbose=true ); # Запустить модель
        engee.close( name_model, force=true ); # Закрыть модель
    end
    sleep(5)
    return model_output
end
Out[0]:
run_model (generic function with 1 method)

The starting conditions will be set as follows:

L = 1.0e6

p(0) = 1.0e5

r, we will change it during the modeling process:

  1. 1.5e-6 (the system converges)
  2. 2.2e-6 (2-cycle system)
  3. 2.5e-6 (4-cycle system)
  4. 2.56e-6 (8-cycle system)
In [ ]: 
L = 1.0e6;
p0 = 1.0e5;
r_arr = [1.5e-6,2.2e-6,2.5e-6,2.56e-6];

Let's run the model in a loop changing the value of r.

In [ ]: 
Population = zeros(21,4)
r = 0;
for i in 1:4  
    r = r_arr[i]
    run_model("population") # Запуск модели.
    P = collect(simout["population/Rounding Function.1"]);
    Population[:,i] = P.value
end 

Building...
Progress 100%
Building...
Progress 100%
Building...
Progress 100%
Building...
Progress 100%

Let's display and compare the results.

In [ ]: 
plot(Population, label=["r = 1.5e-6" "r = 2.2e-6" "r = 2.5e-6" "r = 2.56e-6"])
Out[0]:

Conclusion

According to the results of the model, we see that the ideal population is 1 million people, and with a coefficient of 1.5e-6. In other cases, we observe a numerical increase in the population, which is naturally followed by its decline. In the case of a shortage of resources, and the higher the r coefficient, the greater the diversity in population growth rates.

Blocks used in example