Pipeline pressure control using Chart unit
In this example we will create control logic for pipeline pressure control. To create the algorithm we will use the Chart block of the finite automata library.
Working principle
Detailed description of the pipeline model is considered in the example on the following path:/user/start/examples/physmod/liquid_pressure_regulator. In this case we will briefly describe the model and focus on the points necessary for control.
The structure diagram of the model is presented below and also in the model hydro_control_chart.engee.
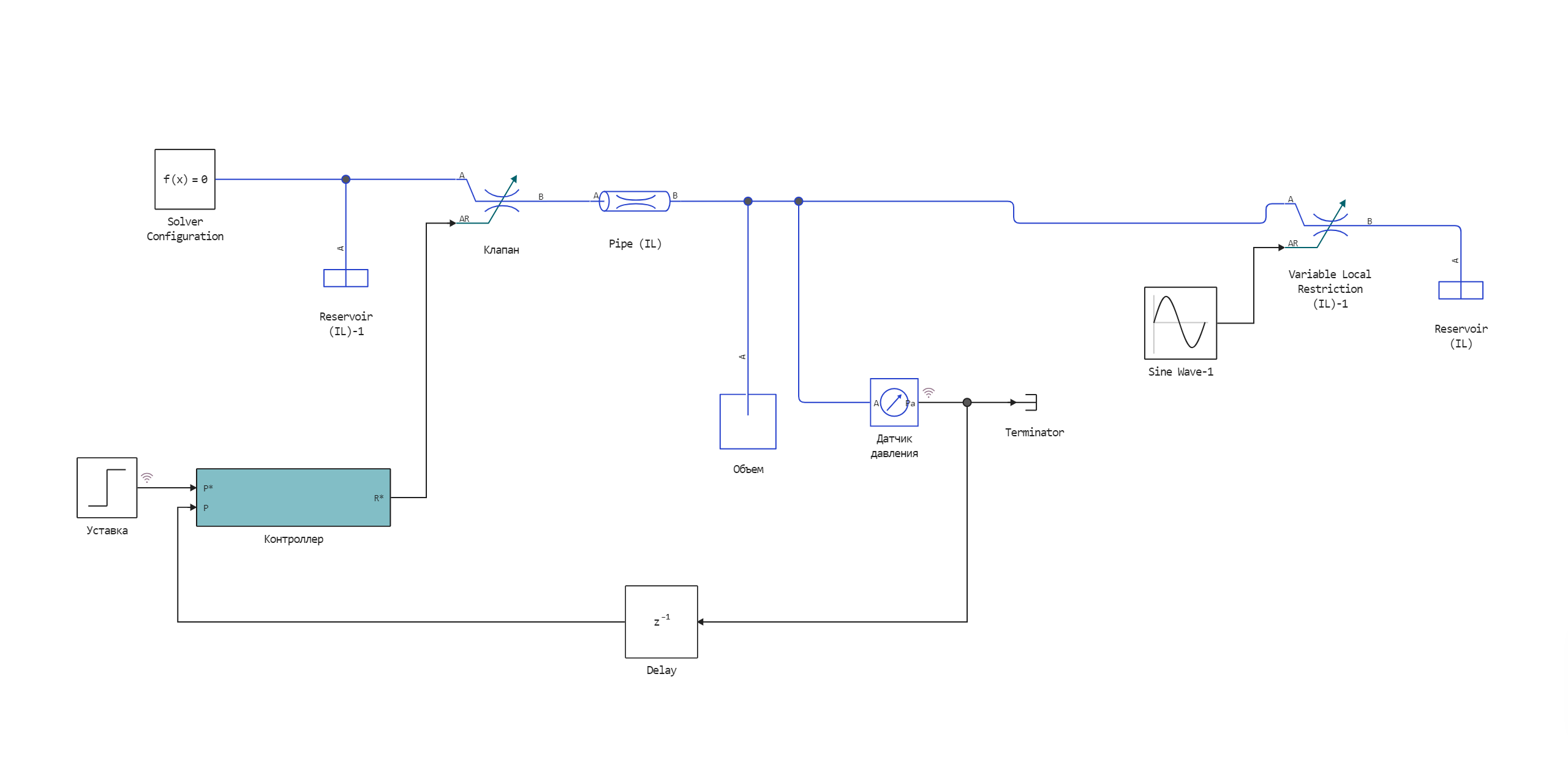
We need to maintain the pressure in the Volume block. The change in pressure is due to accidental leakage. There is a Pressure Sensor in the circuit to measure the pressure. The pressure needs to be maintained according to the Setting.
Control logic
The Controller inputs two signals: setpoint and sensor value. The signal from the Controller output is input to the Valve. This signal determines the cross-sectional area.
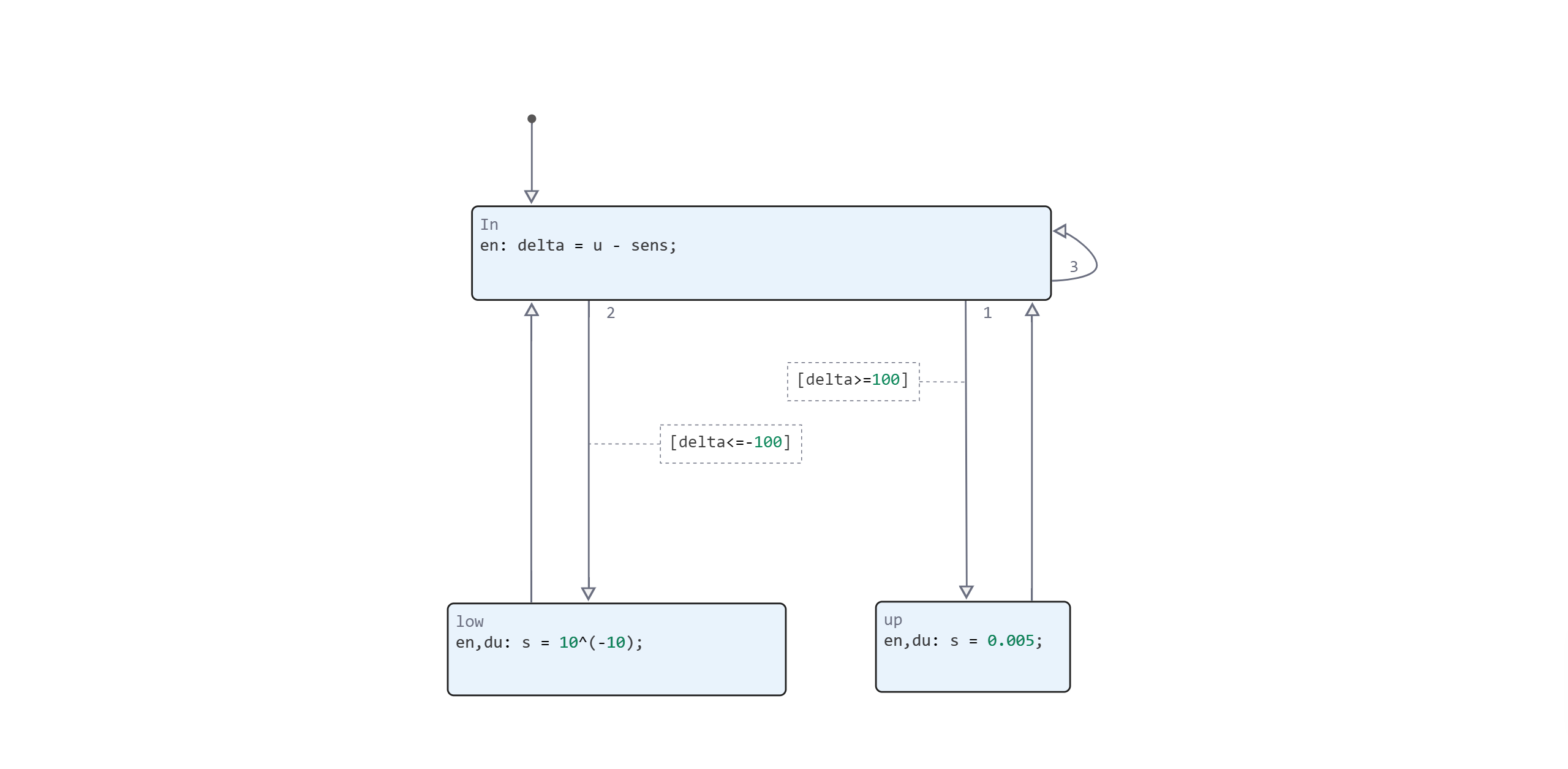
The Chart block of the Controller contains three states. In the initial state, the difference between the set pressure and the measured pressure is determined. Then three transitions are possible.
- To the state
low, if the difference is negative and exceeds the set threshold. In this case we minimise the cross-sectional area of the orifice; - To the state
up, if the difference is positive and exceeds the set threshold. Set the maximum cross-sectional area; - If the error is within the requested value, we stay in the initial state.
Let's run the model and plot the graphs to evaluate the results.
Defining the function to load and run the model
Start the code cell to generate the function to run the model.
function start_model_engee()
try
engee.close("hydro_control_chart", force=true) # закрытие модели
catch err # в случае, если нет модели, которую нужно закрыть и engee.close() не выполняется, то будет выполнена её загрузка после catch
m = engee.load("$(@__DIR__)/hydro_control_chart.engee") # загрузка модели
end;
try
engee.run(m) # запуск модели
catch err # в случае, если модель не загружена и engee.run() не выполняется, то будут выполнены две нижние строки после catch
m = engee.load("$(@__DIR__)/hydro_control_chart.engee") # загрузка модели
engee.run(m) # запуск модели
end
end
Obtaining modelling results
Let's run the simulation of the model using the function generated above.
try
start_model_engee()
catch err
end;
Let's write the logged signals to the variable simout. And convert them into a data array.
result = simout;
res = collect(result)
Let's write the values from the pressure sensor and the setpoint value to the variables.
control_signal = collect(res[1])
pressure = collect(res[2])
Visualisation of the obtained data
using Plots
plot(control_signal[:,1], control_signal[:,2], label="Уставка")
plot!(pressure[:,1], pressure[:,2], label="Датчик давления")
At 5 seconds into the simulation, the setpoint pressure increased to 120 kPa. The pipeline pressure reached the setpoint pressure at approximately 10 seconds and was around the set threshold 100 Pa.
Conclusion
In this example we have demonstrated pressure control in a pipeline using the control logic implemented in the Chart block.